Единичные направления в кристаллах

Принцип вывода 32 классов симметрии.

Теоремы о сочетании элементов симметрии и следствия из них.

• 1. Осевая теорема Эйлера - Равнодействующей двух пересекающихся осей симметрии является третья ось, проходящая через точку их пересечения.

• Частные случаи:

• 1) если есть поворотная ось симметрии порядка n и перпендикулярно этой оси проходит поворотная ось 2-го порядка, то всего имеется n осей 2-го порядка;

• 2) если под углом a пресекаются две поворотные оси 2-го порядка, то перпендикулярно им проходит поворотная ось с элементарным углом поворота в 2 раза большим угла пересечения (2a).

• 2. Точка пересечения оси симметрии второго порядка (L2) или четной оси симметрии с перпендикулярной ей плоскостью симметрии есть центр симметрии. Обратная теорема: Если есть центр симметрии и через него проходит плоскость симметрии, то перпендикулярно этой плоскости через центр симметрии проходит двойная ось симметрии.

• 3. Линия пересечения двух плоскостей симметрии является осью симметрии, причем, угол поворота вокруг оси вдвое больше угла между плоскостями. Следствия: 1) в присутствии оси симметрии порядка n и плоскости, проходящей вдоль оси, всего имеем n таких плоскостей;

• 2) Плоскость, проходящая вдоль инверсионной оси симметрии 3-его и 4-го порядков, приводит к появлению оси 2-го порядка, перпендикулярной инверсионной оси и проходящей по биссектрисе угла между плоскостями.

•

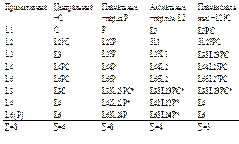Русский кристаллограф А.В. Гадолин в 19 в математически доказал, что в кристаллических многогранниках, тело которых строго ограниченно и зависит от внутреннего строения кристаллов, элементы симметрии наблюдаются в определенных комбинациях. Таких комбинаций элементов 32. Их назвали классами, или видами симметрии. Разделение кристаллов на 32 класса лежит в основе классификации геометрических форм кристаллов.

Единственное, не повторяющееся в кристалле направление называется единичным. Повторяющиеся в кристалле направления, связанные элементамисимметрии, называются симметрично-равными. Положение единичных направлений относительно элементов симметрии: 1. В присутствии единичных направлений возможен центр симметрии, лежащий в середине фигуры. 2. Единичное направление может располагаться перпендикулярно плоскости симметрии или быть совмещенным с ней. 3. Единичное направление может располагаться перпендикулярно оси симметрии второго порядка или может быть совмещено с осью любого порядка. Единичные направления в кристаллах могут либо присутствовать, либо отсутствовать. Соответственно этому и вывод видов симметрии делится на две части. В первой рассматриваются виды симметрии для кристаллов с единичными направлениями, во второй – для кристаллов без них

Дата добавления: 2015-03-29