I. Закон и изотонический коэффициент Вант-Гоффа

Расчетные формулы

Где:

Þ – концентрация растворенного вещества;

Þ Т – температура раствора 0^оС (273 К);

Þ R – универсальная газовая постоянная, не зависящая от природы газа. В системе СИ R=8,31410³ Дж/(кмольК) или R=8,314Дж/(мольК).

Следовательно, осмотическое давление идеального раствора равно тому давлению, которое оказывало бы растворенное вещество, если бы при данной температуре оно в виде газа занимало объём раствора ( осмотический закон Вант- Гоффа).

Пример: 1 М раствор 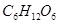. Определите .

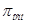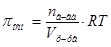
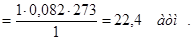или .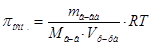

Примечание: Ч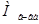ем ­ , тем (например, белки).

Изотонический коэффициент (i) Вант-Гоффа. Степень диссоциации и связь между и

Изотонический коэффициент показывает, во сколько раз возрастает концентрация ионов за счет диссоциации электролита. В растворах электролитов вследствие электролитической диссоциации и увеличения числа частиц опытное осмотическое давление всегда больше, чем теоретически вычисленное по уравнению: 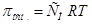. Степень отклонения наблюдаемого осмотического давления 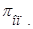от теоретически вычисленной величины 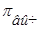выражается изотоническим коэффициентом (i) т.е. . Поэтому при вычислении осмотического давления растворов электролитов в уравнение вводят поправочный (изотонический) коэффициент:

Причем:

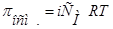
Ассоциация молекул вещества – причина понижения значений коллигативных свойств по сравнению с вычисленными значениями (например, As₂S₃).

Значение его увеличивается по мере разбавления электролита, приближаясь к определенному пределу для каждого отдельного электролита.

или

В общем случае при распаде электролита с образованием К-ионов формула имеет вид:

Если при диссоциации молекулы образуется два иона: 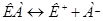, то К=2 и формула примет простой вид:

	или

При вычислении степени диссоциации сильных электролитов говорят не об истинной, а о «кажущейся» степени диссоциации вещества в растворе, т.к. при опытном определении степень диссоциации сильных электролитов всегда оказывается меньше 100%. Это объясняется проявлением электростатического притяжения между ионами, вследствие чего активность их уменьшается и создается видимость неполной диссоциации.

Осмолярная и осмоляльная концентрация в практической медицине

Осмолярная концентрация раствора х арактеризует содержание подвижных частиц в миллиосмолях в 1 л раствора / 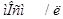/, а осмоляльная концентрация – в 1 кг растворителя / /. Биологические среды (сыворотка крови и моча) – это относительно разбавленные системы, поэтому разница между осмолярностью и осмоляльностью незначительная, т.е. эти термины взаимозаменяемые. Определяется криометрией.

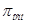внутри и вне клетки одинаково, т.е. осмоляльность внутриклеточной жидкости равна осмоляльности плазмы крови. 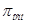крови человека соответствует осмолярная концентрация частиц от 290 до 300 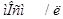. Такое состояние – изоосмия.

Осмолярная концентрация с вязана с его молярной концентрацией через изотонический коэффициент:

Дата добавления: 2015-03-29