Основные теоретические положения. Зависимость тока, протекающего через резистивный элемент от напряжения, приложенного к его выходным зажимам

Зависимость тока, протекающего через резистивный элемент от напряжения, приложенного к его выходным зажимам, называется вольтамперной характеристикой (ВАХ)

.

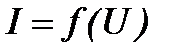Иногда такой зависимостью служит

.

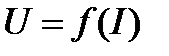Если график ВАХ является прямой линией, то такой элемент называется линейным резистивным элементом (рис. 1). На примере рис. 1 можно графически представить сущность понятия о линейном 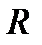– элементе. Какое бы напряжение ни было приложено к его выходным зажимам ( 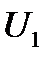и 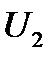) ток всегда будет таким ( 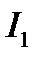или 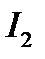соответственно), что отношение

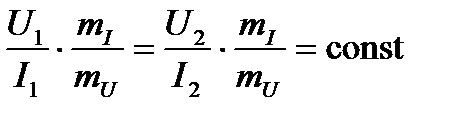
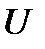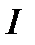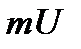есть постоянная величина, не зависящая от и ( и 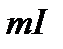– масштабы осей напряжения и тока. Приведенное соотношение с учетом масштабов определяет отношение отрезков, соответствующих напряжению и току по осям координат рис. 1). Учитывая, что для такого резистивного элемента справедлив закон Ома:

,

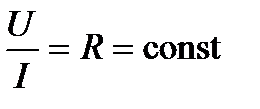получим

.

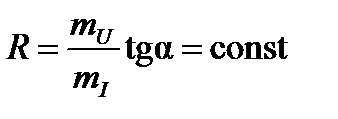То есть для линейного резистивного элемента его параметр 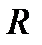(сопротивление) не зависит от режима работы электрической цепи, в которую он включён (или говорят, что он не зависит от тока и напряжения на нем).

Если ВАХ не является прямой линией, то такой резистивный элемент будет нелинейным резистивным элементом (рис. 2). Нелинейность зависимости 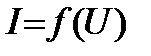связана с тем, что при изменен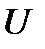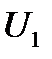и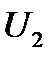и ( и 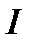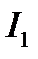) и ( и 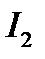соответственно) изменяется их отношение

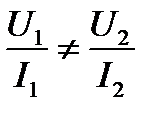или .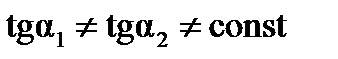

То есть сопротивление нелинейного резистивного элемента не является постоянной величиной и изменяется с изменением и .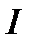

В общем случае нелинейный элемент нельзя характеризовать каким-либо постоянным сопротивлением 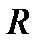и его характеристикой служит ВАХ, задаваемая таблично, графически (рис. 2) или аналитически.

По аналогии с резистивным элементом можно упомянуть о линейных и нелинейных индуктивном (рис. 3) и ёмкостном (рис. 4) элементах электрических схем, в зависимости от того зависят или не зависят их параметры 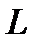(индуктивность) и 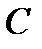(ёмкость) от режима работы элементов.

Разнообразные электронные, ионные, полупроводниковые и магнитные приборы, нашедшие широкое применение в радиотехнике, автоматике, связи, электротехнике обладают свойствами нелинейных элементов. Это вынуждает разрабатывать методы расчёта нелинейных цепей. Цепь является нелинейной, если ее схема замещения содержит хотя бы один нелинейный элемент.

К нелинейным электрическим цепям применимы основные законы электрических цепей, т. е. обобщенный закон Ома и законы Кирхгофа (для цепей переменного тока эти законы справедливы только в мгновенной форме записи). В то же время расчёт нелинейных электрических цепей значительно труднее, чем линейных цепей. Объясняется это тем, что кроме токов и напряжений, подлежащих обычно определению, неизвестными являются зависящие от них сопротивления нелинейных элементов.

Для расчёта нелинейных электрических цепей применяются различные методы расчёта: аналитические, графо-аналитические, графические, которые выбираются в зависимости от способа представления ВАХ, сложности схемы, формы питающего напряжения и, самое существенное, от точности, предъявляемой к результатам расчета. Наибольшее распространение получили графо-аналитические методы расчета таких цепей. Среди них широко известным является метод кусочно-линейной аппроксимации ВАХ элементов. Сущность метода сводится к замене нелинейного элемента линейным или группой линейных, имеющих постоянное сопротивление. Преобразуя таким образом все нелинейные элементы, нелинейную цепь сводят к линейной. Последнюю рассчитывают известными методами.

В самом простейшем случае (рис. 5), если 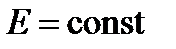, то напряжение на зажимах нелинейного элемента 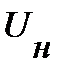и ток, протекающий через, него 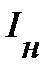также будут постоянными и сопротивление элемента (если оно зависит только от напряжения и тока) также будет постоянным. В этом случае нелинейный элемент можно заменить линейным элементом (рис. 6) с сопротивлением 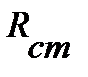, где 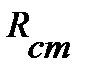– статическое сопротивление нелинейного элемента в точке 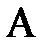его ВАХ (рис. 7), определяемое, как отношение напряжения на элементе к току через него, также определяемые в этой точке

.

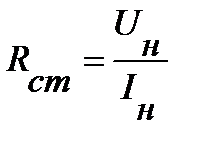Статическое сопротивление можно определить и графически: как тангенс угла между прямой, проведённой из начала координат через точку 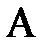на ВАХ и осью токов (рис. 7)

.

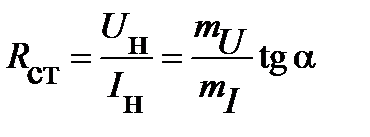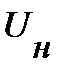Точка на ВАХ, одновременно отвечающая значениям напряжения и 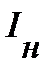на нелинейном элементе, называется рабочей точкой.

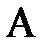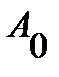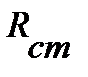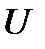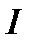Пусть рабочая точка на ВАХ нелинейного элемента изменяет своё положение под действием переменного напряжения, например, колеблется во времени вокруг некоторого среднего положения (рис. 8). В этом случае изменения тока и напряжения нельзя сопоставить с помощью конкретного параметра , поскольку эта величина также изменяется. В то же время, если изменения и невелики, то можно ввести понятие о дифференциальном сопротивлении 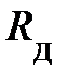. Под ним понимают отношение бесконечно малого приращения напряжения к соответствующему приращению тока (рис. 7)

.

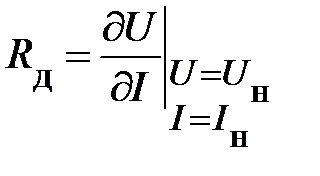Отсюда следует, что, строго говоря, дифференциальное сопротивление характеризует нелинейный элемент в точке ВАХ, для которой оно определяется.

Тем не менее, поскольку для рассматриваемого случая (рис. 8) колебания напряжения (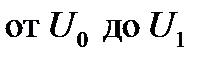 или 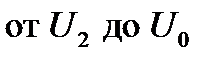) невелики, с достаточной для практики точностью можно считать, что каждая точка участка ВАХ от 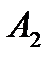до 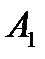характеризуется постоянной величиной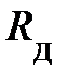

.

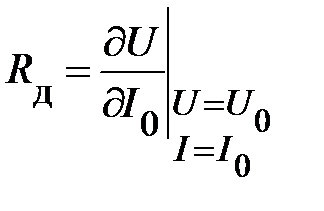Дифференциальное сопротивление можно определить и графически, как тангенс угла между касательной в рабочей точке ВАХ и осью токов (рис. 8) в направлении от оси токов до касательной по часовой стрелке:

.

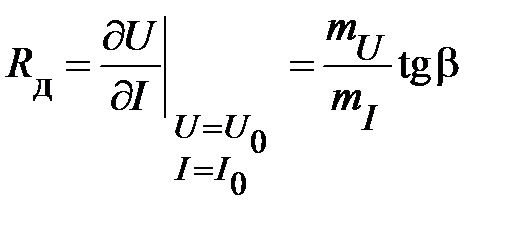Вернёмся к рассматриваемому случаю. Поскольку ВАХ на участке 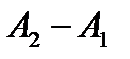заменяется прямой линией, то напряжение 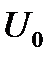можно представить в виде суммы двух слагаемых (рис. 8):

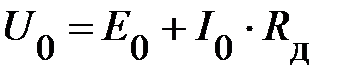. (1)

Учитывая, что со временем положение рабочей точки изменяется в пределах 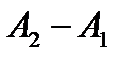к соотношению (1) необходимо добавить слагаемое 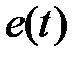, которое определяет некоторый источник ЭДС переменного тока 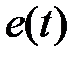с амплитудным значением по напряжению 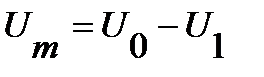или 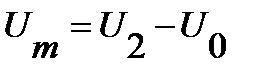. Тогда выражение напряжения на нелинейном 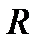– элементе 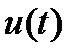примет вид

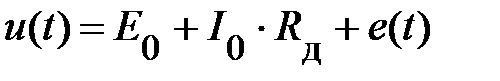. (2)

Соотношение (2) определяет схему замещения нелинейного резистивного элемента (рис. 9), в которой он заменяется линейным резистивным элементом с сопротивлением 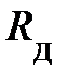и двумя источниками постоянной и переменной ЭДС. Если параметры рабочей точки изменяются в широких диапазонах, то всю ВАХ разбивают на участки, в пределах которых ее можно считать прямой линией (с допустимой степенью точности)

Рассмотренные приёмы называются кусочно-линейной аппроксимацией ВАХ нелинейного элемента. Эти приёмы позволяют, при указанных условиях, свести нелинейную цепь к линейной.

В случае повышенных требований к точности расчёта используют аналитические методы расчета. Они основаны на аналитической аппроксимации ВАХ на всем ее диапазоне возможного изменения (как правило, используется аппроксимация ВАХ 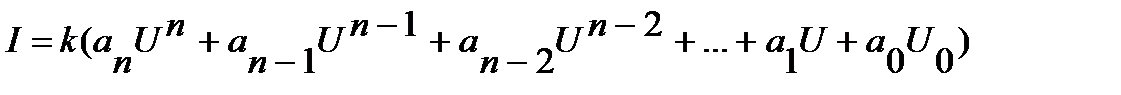в виде полинома от степени 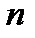, где 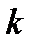– некоторый коэффициент, «уравнивающий» единицы измерения правой и левой части полинома. Выражения для тока 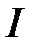в таком виде непосредственно включаются в систему уравнений, описывающих состояние нелинейной цепи (ее режим работы) по методу законов Кирхгофа. Система расчетных уравнений получается нелинейной и для ее решения используют специальные методы, как правило, с использованием ЭВМ (например, методы итерации). Данные методы отличаются сложностью в постановке задачи и ее решения. Однако они обладают максимальной точностью решения и возможностью проведения анализа этого решения (предсказания поведения цепи в широком изменении параметров ее режима работы).

Такими же возможностями (в принципе) обладают и графические методы расчета нелинейных цепей. Однако их точность ограничивается погрешностью графических построений при ведении расчетов. Рассмотрим графический метод преобразований и расчёта цепей с нелинейными элементами, основанный на предварительной замене электрической цепи цепью, имеющей эквивалентную ВАХ и последующего перехода в процессе расчёта к заданной электрической цепи.

Положим, что нелинейные элементы соединены последовательно (рис. 10) и имеют известные ВАХ (рис. 11). Если задан ток в такой цепи (например, 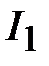на рис. 11), то, т.к. при последовательном соединении элементов ток в каждом элементе будет одинаковым и равным 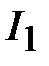, падение напряжения на каждом элементе ( 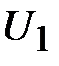и ) находится непосредственно по ВАХ этого элемента без каких-либо дополнительных построений (рис. 11). Если же задано общее напряжение 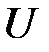, то без дополнительных построений определить в таком соединении элементов (рис. 10) ток и падения напряжения достаточно сложно. Для этого необходимо построить эквивалентную ВАХ. Построение эквивалентной ВАХ основано на следующих особенностях последовательного соединения элементов (рис. 10):

– ток 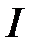в такой цепи, протекающий через каждый элемент один и тот же

;

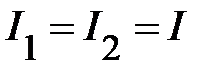– общее напряжение, приложенное ко всей цепи, равно сумме падений напряжени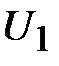й и 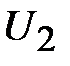на каждом элементе

.

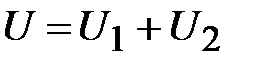Из сказанного следует, что при любом произвольно взятом токе, соответствующая точка эквивалентной ВАХ 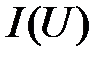находится суммированием абсцисс точек исходных ВАХ 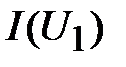и , определённых при том же токе.

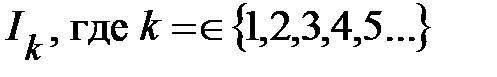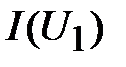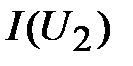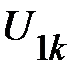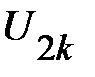Данное правило позволяет следующим образом построить эквивалентную ВАХ (рис. 12). Задаются несколькими произвольно взятыми значениями тока в цепи ( по оси ординат на рис.12); по исходным ВАХ , находят соответствующие каждому току напряжения на этих ВАХ и . Суммированием 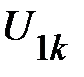и 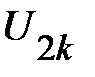определяют абсциссы точек 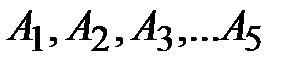эквивалентной ВАХ. Их ординаты заданы произвольно выбранными точками 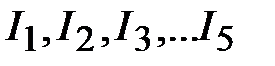. Соединяя плавной линией полученные точки , получают график эквивалентной ВАХ .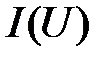

Теперь зная, например, что 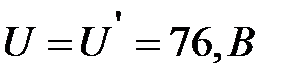, по эквивалентной ВАХ 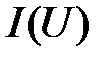определяют ток 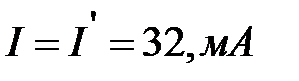, а затем по исходным ВАХ 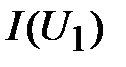и 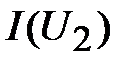находят падение напряжения на каждом элементе 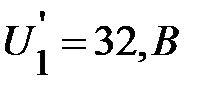, 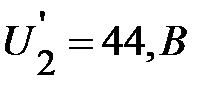. Т.о. производится графический расчёт параметров режима работы цепи из последовательно соединённых нелинейных резистивных элементов.

В случае если один из последовательно соединённых резистивных элементов является линейным (рис. 13), графический расчёт производят методом нагрузочной характеристики.

Пусть дана схема (рис. 13), в которой 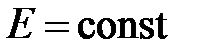, 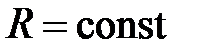. Для неё согласно 2-го закона Кирхгофа можно записать:

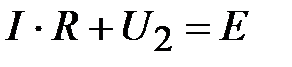
или

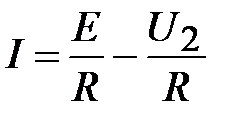. (3)

При постоянных 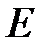и 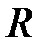соотношение (3) есть уравнение первой степени 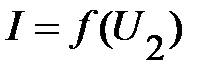, т.е. между 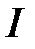и 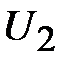в этом случае существует линейная зависимость, которая называется нагрузочной характеристикой. Нагрузочную характеристику строят по двум точкам, которые определяют из условий:

1. при 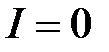, получаем из (3) 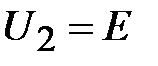(первая точка);

2. при 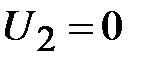имеем 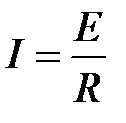(вторая точка).

Проведя через эти точки прямую линию, получаем нагрузочную характеристику (рис. 14). Ток во всех элементах при последовательном соединении (рис. 13) имеет одинаковое значение, которое должно удовлетворять как нагрузочной характеристике 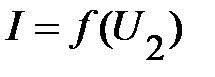, так и ВАХ нелинейного элемента 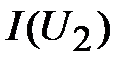. Следовательно, точка их пересечения (т. А на рис. 14) определяет режим работы цепи и является рабочей точкой. С помощью точки А определяют параметры режима работы цепи , ; .

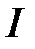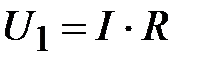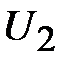Положим теперь, что нелинейные резистивные элементы включены параллельно (рис. 15) и имеют известные ВАХ (рис. 16). Если напряжение в такой цепи (например, 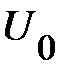на рис. 16) известно, то, т. к. напряжения на всех ветвях параллельного соединения одинаковы (и равны 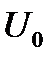), токи через нелинейные элементы ( 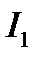и ) находятся непосредственно по соответствующим ВАХ без каких-либо дополнительных построений (рис. 16).

Если же задан общий ток 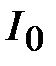, то без дополнительных построений определить в таком соединении элементов (рис. 15) напряжение 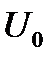и токи в ветвях и 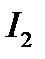достаточно сложно. Для этого необходимо построить эквивалентную ВАХ

.

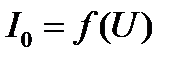Построение эквивалентной ВАХ основано на следующих особенностях параллельного соединения элементов (рис. 15):

· напряжения на каждой ветви параллельного соединения элементов равны друг другу и равны общему напряжению 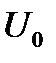, приложенному к такой цепи

;

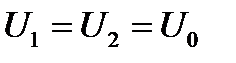· общий ток 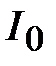во всей цепи равен сумме токов 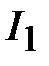и 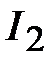в каждой ветви в отдельности

.

Из сказанного следует, что при любом произвольно взятом напряжении 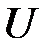соответствующая точка эквивалентной ВАХ 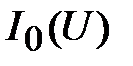находится суммированием ординат точек исходных ВАХ 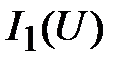и 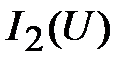, определённых при том же .

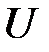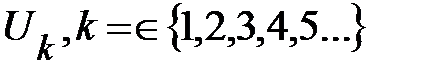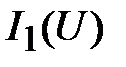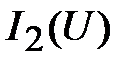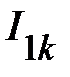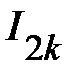Данная особенность позволяет следующим образом построить эквивалентную ВАХ (рис. 17). Задаются несколькими произвольно взятыми значениями напряжения () по оси абсцисс (рис. 17). По исходным ВАХ и находят соответствующие каждому напряжению токи и . Суммированием 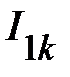и 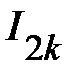определяют ординаты точек 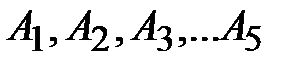, лежащих на эквивалентной ВАХ. Их абсциссы заданы произвольно выбранными напряжениями 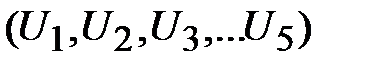. Соединяя плавной линией полученные точки 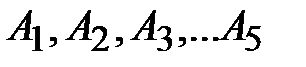, получают график эквивалентной ВАХ .

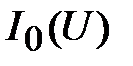Теперь, зная, например, что 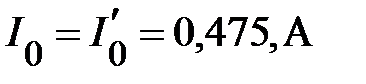, по эквивалентной ВАХ 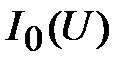определяют напряжение, приложенное к цепи 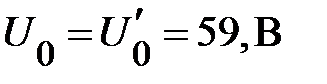, а затем по исходным ВАХ 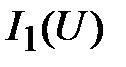и 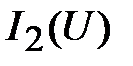находят токи, протекающие через каждый нелинейный резистивный элемент 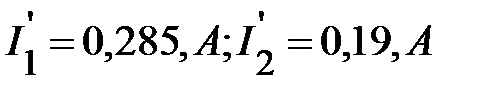(рис. 17). Таким образом, производится расчёт параметров режима работы цепи с параллельным соединением нелинейных резистивных элементов.

В случае если цепь содержит 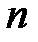нелинейных элементов, соединённых последовательно или параллельно, то расчёт производится аналогично рассмотренным случаям. При этом построение эквивалентной ВАХ производится суммированием точек всех 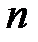исходных ВАХ, соответственно, по напряжению или по току.

В более сложных электрических цепях, например, при смешанном соединении нелинейных элементов эквивалентную ВАХ строят поэтапно. Выделяют в схеме те элементы, которые соединены последовательно или параллельно и начинают расчёт с построения эквивалентной ВАХ для этих элементов. В качестве примера рассмотрим расчёт цепи, схема которой приведена на рис. 18, а исходные ВАХ нелинейных элементов 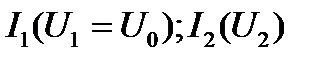и – на рис. 19. В схеме (рис. 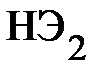18) можно выделить только элементы и 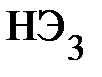, которые соединены последовательно. Других комбинаций элементов с простейшим соединением в схеме нет. Поэтому построение ВАХ эквивалентной такому соединению элементов (рис. 18) начинают с построения промежуточной эквивалентной ВАХ. Эту ВАХ 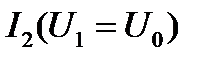получают указанным выше способом, суммируя абсциссы точек исходных ВАХ 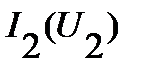и 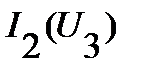. Построение эквивалентной ВАХ 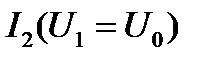схематично означает, что последовательное соединение элементов 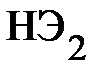и 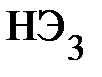эквивалентно заменяется одним элементом 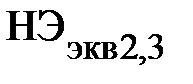, который имеет ВАХ 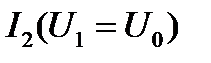(рис. 19).

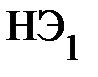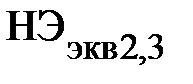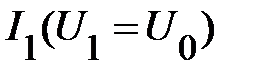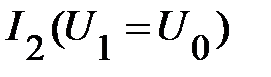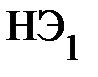Рассматривая вновь полученную схему (рис. 20), видим, что в ней элементы и соединены параллельно. Т. е. можно построить эквивалентную ВАХ для такого соединения, используя графики и , как исходные. Построение проводим, указанным выше способом, суммируя ординаты исходных ВАХ. В результате получаем график . Такое построение схематично означает, что параллельное соединение элементов и 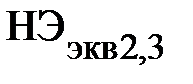эквивалентно заменяется одним элементом 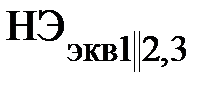(рис. 21), имеющим ВАХ .

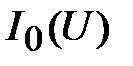Т. о. путём указанного поэтапного построения промежуточных ВАХ построена общая ВАХ всей цепи .

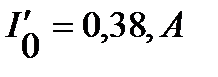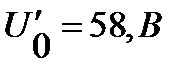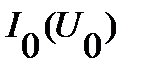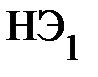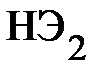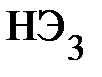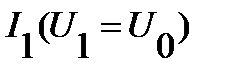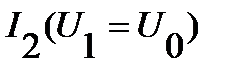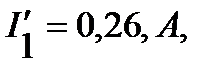
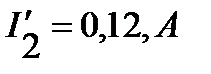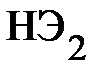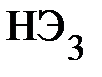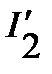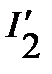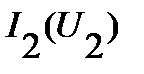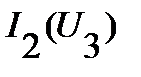Теперь, при заданном общем токе, например, , определяем общее падение напряжения по ВАХ (рис. 19). Это напряжение приложено к элементу и к общим элементам и , следовательно, используя ВАХ и определяем токи . Ток, протекающий через и один и тот же и равен , поскольку они соединены последовательно. Используя значение , определяем с помощью ВАХ и значения напряжений на 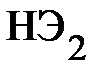и , .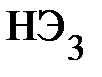

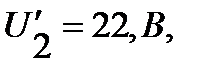
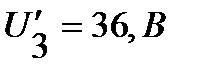Таким образом, используя графические построения, рассчитали параметры режима работы данной цепи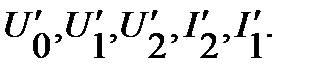

Аналогичным образом проводится расчёт смешанных соединений другой конфигурации.

Дата добавления: 2015-05-06