
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные теоретические положения. Результаты эксперимента по исследованию II закона Кирхгофа
|
|
|
|
ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА МЕТОДА НАЛОЖЕНИЯ
Результаты эксперимента по исследованию II закона Кирхгофа
Результаты эксперимента по исследованию I закона Кирхгофа
| № опыта | Результаты измерений (показания измерительных приборов) | Результаты вычислений | |||||||||
| pA0, A | pA1, A | pA2, A | pA3, A | V, B | R 1, Ом | R 2, Ом | R 3, Ом | R э, Ом | R эт, Ом | δ, % | |
| Первый опыт | |||||||||||
| Второй опыт |
Таблица 2
| Наименование опыта | Данные измерений | Данные вычислений | ||||||
| V | pA1 | pA2 | pA3 | R вн1 | R вн2 | ∑ IR | δ | |
| B | A | A | A | Ом | Ом | B | % | |
| Ключ К1 замкнут, ключ К2 разомкнут | ||||||||
| Ключ К1 разомкнут, ключ К2 замкнут | ||||||||
| Ключи К1 и К2 замкнуты | ||||||||
| E 1=, B; E 2=, B; R 1=, Ом; R 2=, Ом; R 3=, Ом. |
ЛАБОРАТОРНАЯ РАБОТА № 2
Цель работы: экспериментально исследовать принцип суперпозиции (наложения); получить практические навыки при решении задач методом наложения.
Принцип суперпозиции (наложения) является одним из важнейших физических принципов, отражающих основное свойство линейных систем – независимость действия возбуждающих сил.
Этот принцип используется при рассмотрении явлений, возникающих под воздействием нескольких причин. В соответствии с этим принципом сложные явления подразделяются на более простые, в которых каждая причина действует независимо от других, а результаты воздействий, накладываясь один на другой, образуют суммарный эффект.
Этот принцип можно применить только к линейным цепям. Его формулируют следующим образом: Ток через любой элемент электрической цепи (напряжение на нем) равен алгебраической сумме частичных токов через этот же элемент (частичных напряжений на нем), вызванных действием каждого источника энергии в отдельности.
При анализе сложных электрических цепей принцип суперпозиции используется для того, чтобы воздействие нескольких источников электрической энергии на данный элемент цепи можно было рассматривать как результат воздействия на этот элемент каждого из источников в отдельности.
Отметим, что принцип суперпозиции применяется также для того, чтобы результат воздействия одной ЭДС сложной формы можно было заменить воздействием составляющих ЭДС более простых форм.
Применяя принцип суперпозиции, можно найти ток любой ветви или напряжение любого участка линейной электрической цепи как алгебраическую сумму частичных токов или напряжений, вызываемых отдельным действием источников ЭДС и тока. С помощью принципа суперпозиции (наложения) расчёт сложной цепи с несколькими источниками ЭДС и тока можно свести к расчёту нескольких цепей с одним источником.
Выбирая, поочерёдно, следующий источник энергии для расчёта частичных токов, остальные источники из схемы устраняют. При этом, устраняя источники ЭДС, оставляют их внутренние сопротивления, устраняя источники тока – их внутренние проводимости; место включения источника ЭДС закорачивают, место соединения источника тока разрывают. На рис. 1 – 4 показано, как устраняются из схемы идеальный (рис. 1) и реальный (рис. 2) источники ЭДС, а также идеальный (рис. 3) и реальный (рис. 4) источники тока.
Рассмотрим схему электрической цепи (рис. 5), в которой имеется три источника ЭДС. Для определения токов в такой цепи вначале полагают, что в ней действует только источник ЭДС  . Сопротивления всех элементов считают неизменными. Определение частичных токов
. Сопротивления всех элементов считают неизменными. Определение частичных токов 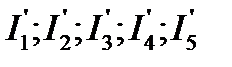 отдельных ветвей от действия источника ЭДС
отдельных ветвей от действия источника ЭДС 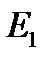 сводят к расчёту цепи, схема которой приведена на рис. 6. Далее проводят расчёт частичных токов
сводят к расчёту цепи, схема которой приведена на рис. 6. Далее проводят расчёт частичных токов  от действия источника ЭДС
от действия источника ЭДС 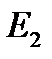 в соответствии со схемой рис.7. и частичных токов
в соответствии со схемой рис.7. и частичных токов  от действия источника ЭДС
от действия источника ЭДС 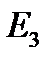 по схеме рис. 8. Алгебраическое суммирование частичных токов с учётом их направлений на схемах (рис. 6 – 8) даёт значения действительных токов ветвей:
по схеме рис. 8. Алгебраическое суммирование частичных токов с учётом их направлений на схемах (рис. 6 – 8) даёт значения действительных токов ветвей:
 . (1)
. (1)
Как видно, метод расчёта электрических цепей с использованием принципа суперпозиций является довольно громоздким и поэтому применяется редко. Он целесообразен тогда, когда электрическое состояние цепи определено для каких – либо источников ЭДС и токов и требуется проанализировать электрическое состояние цепи при изменении ЭДС или тока одного из источников. В этом случае нет необходимости вновь рассчитывать значения токов и напряжений от действия всех источников, а достаточно определить лишь частичные токи и напряжения от действия дополнительной ЭДС 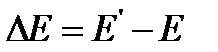 или дополнительного тока
или дополнительного тока  источника. После чего алгебраической суммой определяют реальные токи в цепи при изменении
источника. После чего алгебраической суммой определяют реальные токи в цепи при изменении  или
или  .
.
Пример: На схеме замещения электрической цепи (рис. 9) при заданных значениях 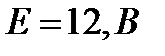 и
и  известны токи всех ветвей:
известны токи всех ветвей: 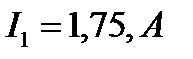 ,
,  ,
,  ,
,  . Требуется проанализировать электрическое состояние цепи при увеличении и уменьшении ЭДС
. Требуется проанализировать электрическое состояние цепи при увеличении и уменьшении ЭДС  в 2 раза, т. е. при новых значениях ЭДС
в 2 раза, т. е. при новых значениях ЭДС  и
и  . Для этого определим частичные токи в ветвях от действия двух новых источников ЭДС
. Для этого определим частичные токи в ветвях от действия двух новых источников ЭДС  и
и 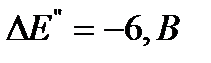 в схеме замещения, показанной на рис. 10. Для схемы рис. 10 при заданных значениях сопротивлений резистивных элементов частичные токи от действия ЭДС
в схеме замещения, показанной на рис. 10. Для схемы рис. 10 при заданных значениях сопротивлений резистивных элементов частичные токи от действия ЭДС  равны:
равны:  ,
,  ,
, 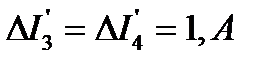 . Именно такие приращения получают токи в ветвях цепи рис. 9 при увеличении в 2 раза ЭДС
. Именно такие приращения получают токи в ветвях цепи рис. 9 при увеличении в 2 раза ЭДС  . После увеличения ЭДС токи примут значения:
. После увеличения ЭДС токи примут значения:
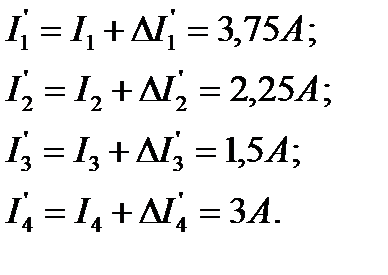
От действия ЭДС  частичные токи будут иметь значения:
частичные токи будут иметь значения: 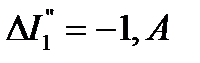 ,
,  , а новые значения токов в ветвях при уменьшении ЭДС
, а новые значения токов в ветвях при уменьшении ЭДС  в 2 раза составят:
в 2 раза составят: 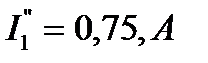 ,
, 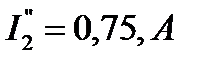 ,
, 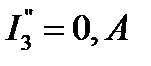 ,
,  . Следует обратить внимание на то, что ток
. Следует обратить внимание на то, что ток  . Это произошло вследствие того, что потенциалы точек
. Это произошло вследствие того, что потенциалы точек 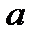 и
и  в схеме рис. 10 при новом значении ЭДС
в схеме рис. 10 при новом значении ЭДС  оказались равными
оказались равными

В заключении подчеркнём, что метод суперпозиций не применим для расчёта мощностей элементов цепи, так как их значения пропорциональны квадратам токов.
|
|
|
|
|
Дата добавления: 2015-05-06; Просмотров: 403; Нарушение авторских прав?; Мы поможем в написании вашей работы!