Синус, косинус и тангенс острого угла в прямоугольном треугольнике

Углы в прямоугольном треугольнике

Рассмотрим прямоугольный треугольник ABC с прямым углом C (рис. 10). Катет BC этого треугольника является противоположным углу A,

а катет AC - прилежащим к этому углу.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Синус, косинус и тангенс угла равного α обозначается символами sin α, cos α и tg α (читается: «синус альфа», «косинус альфа» и «тангенс альфа»). На рисунке

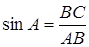, (1)

, (2)

, (3)

Из формул (1) и (2) получаем:

Сравнивая с формулой (3), находим

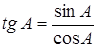(4),

то есть тангенс угла равен отношению синуса к косинусу этого угла.

ТЕОРЕМА. Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

ДОКАЗАТЕЛЬСТВО. Пусть ABC и A₁B₁C₁ - два прямоугольных треугольника с прямыми углами C и C₁ и с одним и тем же углом при вершине A и A₁ равны α (рис. 11).

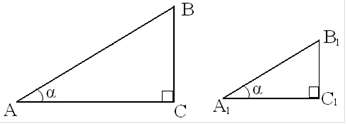
Треугольники ABC и A₁B₁C₁ подобны по первому признаку подобия треугольников, поэтому 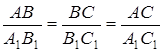. Из этих равенств следует, что 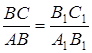, то есть .

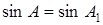Аналогично , то есть , и , то есть .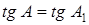

Что и требовалось доказать.

Докажем теперь справедливость равенства

(5).

Из формул (1) и (2) получаем 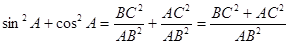. По теореме Пифагора , поэтому .

Равенство (5) называется основным тригонометрическим тождеством.

Представим ещё одно доказательство теоремы Пифагора, основанное на определении косинуса угла в прямоугольном треугольнике.

ДОКАЗАТЕЛЬСТВО. Пусть ABC - данный прямоугольный треугольник с прямым углом C. Проведём высоту CD из вершины прямого угла C. (рис. 12).

По определению косинуса угла . Отсюда 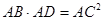. Аналогично . Отсюда .

Складывая полученные равенства почленно, и, замечая, что AD+DB=AB, получим .

Что и требовалось доказать.

Дата добавления: 2015-05-06