Антенных решеток

Акустооптический процессор обработки сигналов

Многофункциональные антенные решетки (АР) являются современными радиоэлектронными комплексами, предназначенными для определения координат и частоты источника электромагнитного излучения в широком интервале углов и большой полосе частот. Решение этой задачи в чисто электронном базисе сталкивается со значительными техническими трудностями. Из антенной техники известно, что распределение комплексной амплитуды электромагнитного поля в апертуре антенны и ее диаграмма направленности связаны пространственным преобразованием Фурье. Этот факт наводит на мысль о возможности применения оптических методов для обработки сигналов ФАР, поскольку в оптических системах пространственное преобразование Фурье осуществляется предельно просто. Первая попытка решения задачи обработки сигналов АР с помощью оптических методов была предпринята Ламбертом в 1965 г.

АОП Ламберта для обработки сигналов, принятых линейной АР, представляет собой, по сути дела, АОСПИ на основе многоканального АОМ (рис.4.6). Сигналы, принятые (2 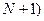элементной АР, после гетеродинирования, фильтрации и усиления поступают на входы 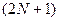)- канального АОМ, помещенного в оптическую систему АОСПИ, в котором выполняется двумерное пространственное преобразование Фурье.

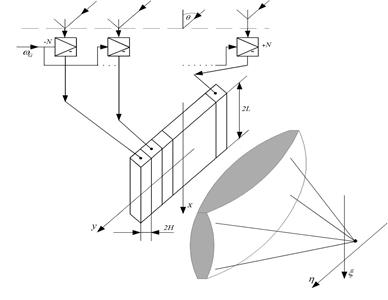
Рис.2.6. Акустооптический процессор для обработки сигналов линейной АР

Для определения характеристик АОП найдем распределение интенсивности в плоскости 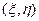регистрации светового распределения. Сигнал, принятый -м элементом АР и поступающий после гетеродинирования на -й канал многоканального АОМ, имеет вид

. (2.11)

Здесь 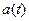и -законы амплитудной и фазовой модуляции в принятом сигнале, 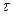-относительная временная задержка сигнала в соседних элементах АР, связанная с направлением на источник соотношением

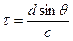, (212)

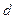-расстояние между элементами АР, 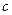-скорость света; 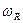-угловая частота принятого сигнала с учетом возможного доплеровского сдвига частоты, 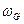-частота общего гетеродина, 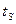-время прихода сигнала на центральный элемент АР. В линейном режиме дифракции световое поле, дифрагирующее (для определенности) в +1 порядок на сумме сигналов вида (2.11), в выходной плоскости АОМ будет иметь вид

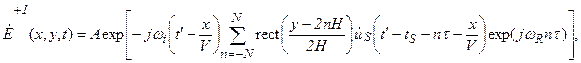
где 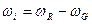-промежуточная частота, близкая к центральной частоте АОМ;

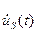-комплексная огибающая сигнала 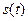: ; 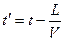- ²смещенное² время, 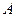-коэффициент, в который включены несущественные сомножители. Функция под знаком суммы учитывает многоканальность АОМ, 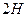-ширина акустического пучка по оси 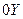. В результате двумерного преобразования Фурье, осуществляемого сферической линзой Л, в ее фокальной плоскости получается распределение комплексной амплитуды светового поля:

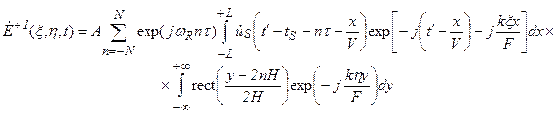. (2.13)

Выполнив интегрирование по переменной 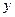и воспользовавшись формулой суммирования геометрической прогрессии

,

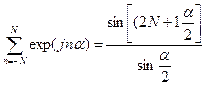образуем выражение для интенсивности дифрагировавшего света

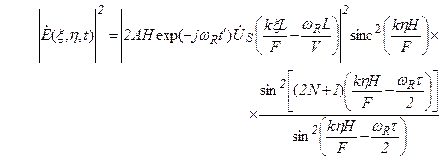. (2.14)

В (2.14) 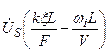-спектр комплексной огибающей сигнала 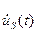, причем в порядке приближения считается, как это принято в теории АР, 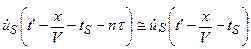, т.е. что комплексная огибающая сигнала не зависит от временной задержки в соответствующем элементе АР. Видно, что двумерное распределение интенсивности света содержит три сомножителя. Первый из них-это амплитудный спектр принятого сигнала, центрированный вокруг пространственной координаты

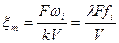, (2.15)

Соотношение (2.15) характерно для АОСПИ и позволяет определить значение несущей частоты принятого сигнала 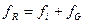с разрешением по частоте, определяемым временной апертурой 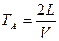АОМ вдоль сигнальной координаты . Второй сомножитель-функция 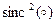отражает факт масштабирования апертуры линейной АР протяженностью 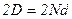в апертуру АОМ вдоль координатной оси 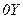с учетом перехода с длины волны 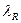, соответствующей радиодиапазону, на оптическую длину волны 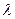. Максимум этой функции расположен при 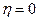, а главный ее максимум имеет ширину но нулям

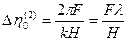. (2.16)

Третий сомножитель вида 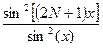описывает спектр периодической решетки конечной протяженности, иначе говоря-диаграмму направленности линейной эквидистантной решетки из 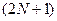элементов. Главный максимум этой функции расположен в точке

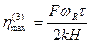. (2.17)

Используя формулу (2.12) и переходя к длинам волн принятого сигнала 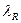и света 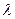, приведем (2.17) к виду

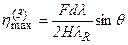. (2.18)

Таким образом, положение главного максимума по оси 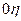определяет направление на источник излучения (пеленг). Ширина этого максимума по нулям, как легко видеть, есть

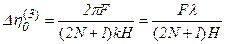, (2.19)

она определяет разрешающую способность процессора по углу прихода сигнала. Действительно, пусть АР принимает два сигнала на одной и той же длине волны 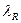с двух различных направлени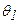й и 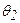(пусть 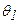> 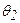). Согласно (2.18) и (2.19) отклики будут разрешимы, если соответствующие максимумы пространственно разнесены по оси 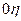не менее чем на . Это значит, что должно быть выполнено условие

,

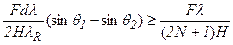которое легко приводится к виду

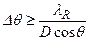. (2.20)

Это соотношение, в котором 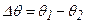, а -среднее направление прихода сигналов, является основным в теории линейных АР. Следовательно, АОП обеспечивает разрешение по углу прихода сигнала характерное для АР с заданной апертурой.

Сравнивая (2.16) и (2.19), видим, что в пределах главного лепестка функции 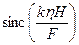размещается 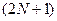лепестков функции 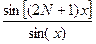. При этом пределы перемещения главного максимума диаграммы направленности согласно (2.18) для углов , изменяющихся от –90⁰ до +90⁰ (обзор полупространства), ограничены областью

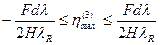. (2.21)

Неравенства (2.21) определяют, таким образом, рабочую область по оси 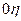. На границах этой области масштабирующая функция 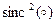принимает минимальное значение

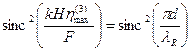. (2.22)

Из антенной техники известно, что для однозначного определения пеленга необходимо, чтобы в зоне видимости имелся бы единственный главный максимум диаграммы направленности. Для этого расстояние между элементами антенной решетки выбирается согласно условию 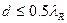. Считая, что это условие выполнено, получаем оценку

,

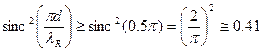которая определяет неравномерность амплитудно-частотной характеристики АОП. В пределах упомянутой рабочей зоны умещается, как нетрудно видеть, количество главных лепестков диаграммы направленности, равное отношению

,

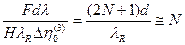что соответствует количеству разрешаемых (по нулевому критерию) угловых дискретных положений глобального максимума диаграммы направленности линейной 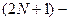элементной АР. Рис.2.7 иллюстрирует приведенные теоретические оценки.

Рис.4.7. Распределение интенсивности света по угловой координате

в выходной плоскости АОП обработки сигналов линейной АР

В обсуждавшемся АОП Ламберта принятые линейной АР сигналы разделяются в оптической системе пространственным образом с помощью многоканального АОМ, т. е. естественным путем. Важным достоинством процессора Ламберта является то, что он позволяет одновременно определять угловые координаты и частоты всех имеющихся в секторе обзора источников. При этом угловое разрешение задается размерами апертуры АР, а частотное разрешение-временной апертурой одиночного канала АОМ. Последнее обстоятельство с учетом того, что временные апертуры реальных АОМ не превосходят нескольких десятков микросекунд, накладывает ограничение на точность определения частоты источника и делает в некоторых случаях невозможным определение доплеровского сдвига частоты. Как отмечалось выше, этот недостаток, присущий всем АОП с пространственным интегрированием, может быть устранен при переходе к процессорам с временным интегрированием.

2.4. Двухмерный АОС с пространственным и временным интегрированием (АОСПВИ).

Двухмерный АОС с пространственно-временным интегрированием (АОСПВИ) сочетает достоинства одномерных АОС с пространственным интегрированием и АОСВИ, позволяя получить полосу анализируемых частот, равную полосе пропускания АОМ, и разрешение по частоте, определяемое временной апертурой АОМ и числом фоточувствительных элементов в строке фотоприемника.

Структурная схема двухмерного АОСПВИ изображена на рис. 4.8

Коллимированный пучок света фокусируется цилиндрической линзой 1 на апертурах АОМ 2, 3, которые возбуждаются первым опорным ЛЧМ сигналом

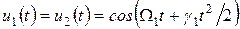. (2.23)

Сферическая линза 4 фокусирует на апертуре АОМ 5 +1-й дифракционный порядок после АОМ 3, а на апертуре АОМ 6 +1-й порядок после АОМ 2. АОМ 5 возбуждается вторым опорным ЛЧМ сигналом u₃(t). Этот сигнал периодический с периодом 2L / V

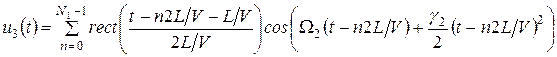, (2.24)

где N₁= T/(2L/V); T – длительность анализируемой выборки сигнала (время накопления фотоприемника); W₂, g₂ – начальные частота и скорость изменения частоты ЛЧМ сигнала.

Анализируемый сигнал u₄(t) поступает на АОМ 6. После АОМ 5 и АОМ 6 в плоскость регистрации пропускаются +1-е дифракционные порядки, которые фокусируются линзой 7 на апертуре двухмерного фотоприемника с накоплением. В качестве фотоприемника может быть использована, например, матрица ПЗС. Плоскость регистрации является плоскостью изображения для АОМ 2, 3 и плоскостью пространственных частот для АОМ 5, 6.

Результирующая амплитуда светового поля в плоскости фотоприемника имеет вид

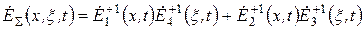, (2.25)

где 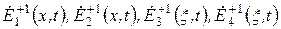– световые поля в первых дифракционных порядках в плоскости фотоприемника для АОМ 2, 3, 5, 6.

Поле 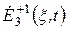по структуре представляет собой набор световых полос, ориентированных вдоль координаты х, с распределением амплитуды поля по координате x в виде функции sinc(*). Частота света от строки к строке изме- няется дискретно с интервалом V/2L, соответствующим разрешению по частоте анализатора спектра с пространственным интегрированием. Световое распределение с такими параметрами играет в устройстве роль оптического гетеродина, осуществляющего перенос частоты в полосу (0... 1/(2 L/V)), в которой производит анализ спектра одномерный АОСВИ.

В результате накопления на фотоприемнике образуется распределение заряда

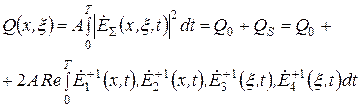, (2.26)

где A – постоянная.

Рис. 2.8. Распределение заряда на ФПУ в направлении оси X (а) и Y (б) в конце цикла накопления

Рассмотрим составляющую заряда Q_S:

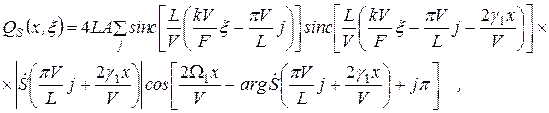(2.27)

где j – номер строки в выходном распределении заряда; –

преобразование Фурье анализируемого сигнала.

На рис. 2.10 представлена структура распределения заряда на ФП (а) и зависимости нормированной величины заряда в направлении осей y (б) и x (в). Распределение заряда Q_S(x, x) имеет форму растра, т. е. системы строк, ориентированных вдоль оси x. По структуре распределение заряда представляет собой пространственное несущее колебание в направлении оси x, промодулированное по амплитуде амплитудным, а по фазе фазовым спектрами сигнала u₄(t). Координаты х и x можно рассматривать как направления точного и грубого отсчетов частоты соответственно. Вдоль оси x – направления грубого отсчета частоты – анализ выполняет АОС с пространственным интегрированием (АОМ 6 и линза 7), а вдоль оси х – направления точного отсчета частоты – АОСВИ на основе АОМ 2, 3.

Найдем отклик анализатора спектра на гармоническое воздействие. Подставив u₄(t)=cosW₀t в (4.11), получим:

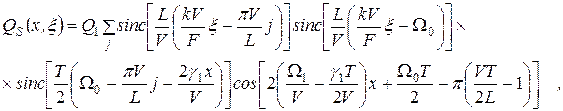(2.28)

где Q₁ – постоянная. Вторая функция sing описывает отклик АОС с пространственным интегрированием, третья функция sing – отклик АОС с временным интегрированием.

Анализируя функции sinс, описывающие отклики анализатора спектра с пространственным интегрированием и с временным интегрированием легко получить формулы для разрешения по частоте по координатам x и x:

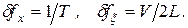(2.29)

Полоса анализа АОС определяется полосой пропускания АОМ 5, 6: Df _A £Df _AOM5,6.

Число элементов разрешения по частоте АОСПВИ:

(2.30)

имеет величину порядка 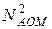, что существенно превосходит соответствующий параметр для одномерных АОС.

Кроме основных видов АОС, рассмотренных выше, известны и другие, которые по своим параметрам занимают промежуточное положение. В целом АОС в настоящее время образуют обширное семейство устройств с богатыми функциональными возможностями.

Рис. 2.10. Структура распределения заряда на ФП (а), зависимость нормированной величины заряда в направлении оси y (б) и распределение заряда вдоль одной из строк растра (в).

Дата добавления: 2015-05-06