Вывод уравнений ВАХ-тик транзистора

Физические процессы в биполярном транзисторе описываются системой уравнений, представляющих собой математическую модель транзистора. Для её построения необходимо получить уравнения, связывающие токи транзистора с действующими на переходах напряжени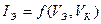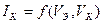й: , и 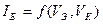. На практике достаточно рассчитать токи эмиттера и коллектора, а ток базы найти из уравнения токов транзистора (3.14). Расчет оков транзистора будем проводить только для бездрейфового транзистора.

Полный ток эмиттера можно найти, суммировав плотности токов электронов j_Эп и дырок j_Эр, протекающих через эмиттерный переход, и умножив результат на площадь эмиттерного перехода S_Э:

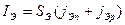. (4.14)

Ток электронов в базе для бездрейфового транзистора переносится только за счет диффузии и плотность тока электронов можно рассчитать на основе (4.4). Дифференцируя (4.10) по х и подставляя производную в (4.4), получим

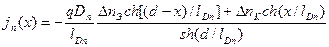. (4.15)

Плотность эмиттерного тока электронов можно определить из (4.15) при х = 0. Исходя из этого и, воспользуясь выражениями (4.7) и (4.8), окончательно имеем:

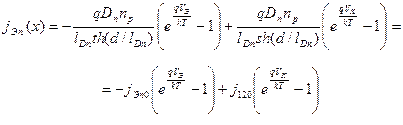, (4.16)

где j_Эп0 и j₁₂₀ – предэкспоненциальные множители.

Плотность дырочной составляющей тока эмиттера можно определить из обычного уравнения вольтамперной характеристики идеализированного р-п перехода:

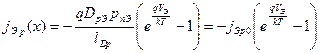, (4.17)

где j_Эр0 - предэкспоненциальный множитель, D_рЭ и р_пЭ – коэффициент диффузии дырок и их концентрация в области эмиттера.

Подставив (4.16) и (4.17) в (4.14) и проведя несложные преобразования, получим уравнение вольтамперной характеристики эмиттерного тока в виде

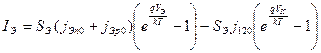. (4.18)

Расчет полного тока коллектора представляет более сложную задачу, так как коллектор имеет (см.рис. 3.1) активную и пассивную области. Площадь активной области коллекторного перехода S_К равна площади эмиттерного перехода S_Э, площадь пассивной области, где также могут происходить перенос тока, равна (S_К – S_Э). Таким образом, коллекторный ток может быть рассчитан по формуле

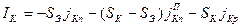, (4.19)

где 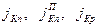- соответственно электронная активной области, электронная пассивной области и дырочная составляющие плотности тока коллектора. В дальнейшем будем предполагать, что с некоторой погрешностью электронные составляющие тока активной и пассивной областей равны.

Электронную составляющую плотности тока определим аналогично току эмиттера из (4.15) при х = d. Имеем

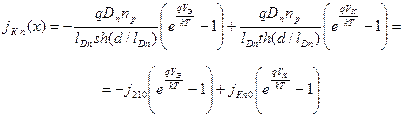, (4.20)

где j_21S и j_КпS – предэкспоненциальные множители. Дырочную составляющую определим также как ток идеализированного р-п -перехода:

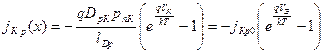, (4.21)

где j_Кр0 - предэкспоненциальный множитель, D_рК и р_пК – коэффициент диффузии дырок и их концентрация в области коллектора.

Подставив аналогично (4.20) и (4.21) в (4.19) и проведя несложные преобразования, получим уравнение вольтамперной характеристики коллекторного тока в виде

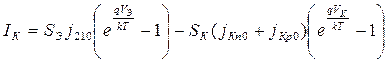. (4.22)

Для анализа физических процессов в биполярном транзисторе уравнения (4.18) и (4.22) представляют в виде:

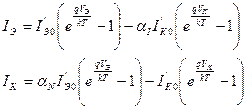, (4.23)

где 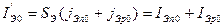- собственный ток насыщения эмиттерного р-п -перехода, 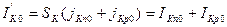- собственный ток насыщения коллекторного р-п -перехода, 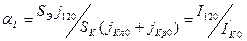- инверсный коэффициент передачи тока и 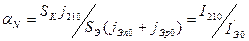- нормальный коэффициент передачи тока. Можно легко показать, что для этих коэффициентов справедливо равенство: .

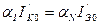Система уравнений (4.23) и представляют собой расчетные вольтамперной характеристики эмиттерного и коллекторного токов транзистора. Отметим, что эти уравнения справедливы только при низких уровнях инжекции, когда число инжектированных в базу электронов значительно меньше, чем число дырок - основных носителей тока в базе. Кроме того, эта система уравнений справедлива для любой схемы включения транзистора и при его работе в любом режиме.

Дата добавления: 2015-05-06