Размерные эффекты и свойства нанообъектов

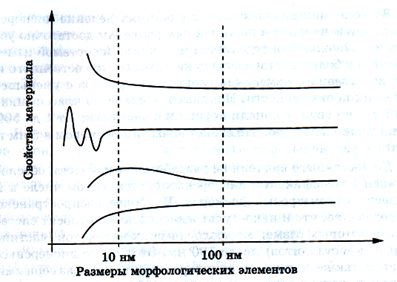
Рис.195 Схематическое изображение вариантов изменения свойств материала при уменьшении размеров его морфологических элементов

Р

На рис.195 схематично показано, что свойства наноматериала при уменьшении его размеров могут увеличиваться, уменьшаться, имеет экстремальную или осциллирующую зависимость. Следует заметить, что размер с которого начинаются изменения, для каждого свойства индивидуален.

Геометрия и размер частиц существенно влияют на характер зависимостей. Так, например, закон всемирного тяготения и закон Кулона для трехмерного пространства имеют знакомый вид

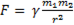и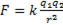

В тоже время двумерного пространства (пленки) эти же законы имеют такой вид

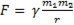и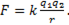

В качестве другого примера рассмотрим зависимость теплоемкости твердых тел Сv от температуры при достаточно низких температурах. Так для массивных материалов согласно теории Дебая Сv~T³, для слоистых структур выполняется закон квадратов (Сv~T²)(например, для графита и галлия), для цепочечных структур (кристаллы селена, HF, BiO₃ и MgSiO₃) имеет место линейная зависимость (Сv~T), т.е. геометрия и размеры объектов влияют те или иные закономерности.

Кристаллическая решетка и магические числа. Большинство металлов кристаллизуются либо плотноупакованную гранецентрированную кубическую ГЦК-решетку (Ag, Al, Au, Cu, Pb, Rh), либо в гексагональную плотноупакованную ГПУ-решетку (Mg, Os,,Re,Zn). Каждый атом в обеих решетках имеет 12 соседей. На рис.196 показаны 12 соседей атома, находящегося в центре куба (выделен черным цветом) для ГЦК- решетки.

Рис. 196 Элементарная ячейка ГЦК решетки, построенная вокруг центрального атома (затемнен), включает 12 его ближайших соседей.

Наименьшая из теоретических наночастица состоящая из 13 атомов имеет вид (рис.196).

Рис.197 13-ти атомная ГЦК наночастица, имеющая форму 14-гранника

На рис.197 показан четырнадцатигранник с минимальным объемом, который образуется соединением этих атомов плоскими гранями, который называется кубооктаэдром. У этого 14-гранника- шесть квадратных граней и 8 граней в форме равностороннего треугольника. Если нарастить на частицу еще один слой, т.е. добавить к этим 13-ти атомам еще 42, то получится частица той же формы из 55 атомов. Добавляя слои к такой частице, можем получить еще большие по размеру частицы. Они, образуют ряд частиц с суммарным количеством атомов N=1, 13, 55, 147, 309, 561,..., которые называют структурными магическими числами. Магические числа означают, что частицы, состоящие из этого количества атомов, более стабильны, чем частицы с числом атомов не равным магическому числу. Такое название магические числа носят потому, что они получаются с минимальным объемом и максимальной плотностью наночастицы с формой близкой к сферической, и плотно упакованной структурой, характерной для объемных тел.

Конфигурации наночастиц, в которых электроны образуют заполненные оболочки, особенно устойчивы и порождают электронные магические числа с N= 3, 9, 20, 36, 61,... для ГЦК структур.

Дата добавления: 2015-05-06