Некоторые сведения о векторах

Величины, характеризующиеся численным значением и направлением, называются векторами. К числу векторов принадлежат скорость, ускорение, сила и ряд других величин. В практике расчетов электрических цепей переменного тока широко используется метод векторных диаграмм, отличающийся простотой и наглядностью. Диаграммы применяют главным образом потому, что сложение и вычитание синусоидальных величин, наиболее просто выполняется в векторной форме. На чертежах векторы изображаются в виде прямолинейных отрезков со стрелкой на конце. Длина отрезка в установленном масштабе дает модуль вектора, а указанное стрелкой направление отрезка дает направление вектора.

Векторы, направленные вдоль параллельных прямых (в одну т ту же сторону или в противоположные стороны), называются коллинеарными.

Векторы, направления которых параллельны одной и той же плоскости, называются компланарными.

Одинаковые по модулю коллинеарные векторы, направленные в одну и ту же сторону, считаются равными друг другу. Равные по модулю коллинеарные векторы, имеющие противоположные направления, считаются отличающимися друг от друга по знаку.

Так, например, между векторами, изображенными на рис.224 и их модулями имеются следующие соотношения:

А = В; А = - С; В = - С;

А = В = С или .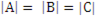

Рис.224

Сложение векторов.

Рис. 225

Пусть даны два вектора А и В (рис.225 а). Чтобы получить результирующий вектор С, перенесем вектор В параллельно самому себе так, чтобы его начало оказалось совмещенным с концом вектора А (рис.225 б). Тогда вектор С, проведенный из начала вектора А в конец вектора В, будет представлять собой результирующий вектор;

С = А + В. (п.1)

Можно, однако, осуществить построение несколько иным способом (рис.225 в). Перенесем вектор В (или А) так, чтобы начала обоих векторов оказались совмещенными. Затем построим на векторах А и В параллелограмм. Диагональ этого параллелограмма, очевидно, совпадает с вектором С, полученным по способу, параллельного переноса (рис. б). По этой причине часто говорят, что векторы складываются по правилу параллелограмма.

Оба рассмотренных способа дают одинаковый результат. Однако в случае сложения более чем двух векторов способ параллельного переноса (способ (б)) оказывается более простым и удобным (менее

Рис.226

загромождается чертеж). Пусть даны векторы А, В, С и D (рис.226). Перенесем векторы параллельно самим себе таким образом, чтобы начало последующего ректора оказалось совмещенным с концом предыдущего.

Получится ломаная линия. Результирующий вектор будет представлять собой вектор Е, проведенный из начала первого из слагаемых векторов А в конец последнего D. Легко убедиться в том, что результирующий вектор Е не зависит от последовательности, в которой складываются заданные векторы. На рис.226 б. показан случай Е = А + В + С + D, а на рис.226 в – случай Е =D+ В + С + А.

Вычитание векторов. Разностью двух векторов А – В называется такой вектор С, который в сумме с

Рис.227

вектором В дает вектор А (рис.227). Поскольку разность А – В может быть представлена в виде

А – В = А + (-В), ( п.2)

вектор С =А –В можно получить, сложив вектор А с вектором, равным по величине вектору В, взятому с обратным знаком.

Радиус – вектор. Радиусом – вектором точки называется вектор, проведенный из начала координат в данную точку (рис.228). Радиус – вектор r однозначно определяет положение точки в пространстве. Его

Рис. 228

декартовым координатам точки:

r_x = x; r_y = y; r_z = z. (п.3)

Квадрат модуля вектора r равен сумме квадратов координат:

r² = x² + y² + z² (п.4).

Проекция вектора на ось. Пусть даны вектор А и некоторое направление в пространстве (ось), которое обозначим буквой n (рис.229). Проведем через начало и конец вектора А плоскости, перпендикулярные к направлению n. Точки 1' и 2', в которых пересекаются эти плоскости с осью n, называются проекциями начала и конца вектора А на ось n. Величина отрезка оси, заключенного между плоскостями, называется проекцией вектора А на направление (или на ось) n. Проекция вектора есть скалярная величина. Если направление от точки 1' к точке 2' совпадает с направлением n, проекция считается положительной; в противном случае проекция отрицательна.

Рис.229

Проекция, обозначается той же буквой, что и сам вектор, с добавлением индекса, обозначающего то направление, на которое спроектирован вектор. Например, проекция вектора А на направление n обозначается А_n.

Введем в рассмотрение угол φ, который образует вектор А с осью n (рис.). Проекция А_n, очевидно, может быть вычислена следующим образом:

А _n = А cosφ, (п.5)

где А – модуль вектора А.

Если вектор образует с данным направлением острый угол, косинус этого угла положителен, проекция вектора также положительна. Если вектор образует с осью тупой угол, косинус этого угла отрицателен, проекция также отрицательна. Если вектор перпендикулярен к данной оси, проекция его равна нулю.

Разложение вектора на составляющие. Каждый вектор А можно заменить несколькими векторами А ₁, А ₂, и т.д., которые в сумме дают вектор А. В этом случае векторы А ₁, А ₂ и т.д. называют составляющими вектора А. Саму операцию замены вектора А несколькими векторами называют разложением вектора А на составляющие.

На рис.230 показано разложение вектора А на составляющие, имеющие направления прямоугольных координатных осей. Символами A_x, A_y, A_z обозначены составляющие вектора А по осям x,y и z.

Рис.230

Дата добавления: 2015-05-06