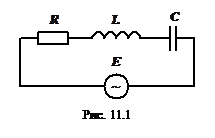
Введение. Рассмотрим процессы, протекающие в колебательном контуре (КК), подключенном к источнику гармонической ЭДС (рис. 1):

Рассмотрим процессы, протекающие в колебательном контуре (КК), подключенном к источнику гармонической ЭДС (рис.1):

Е = Е ₀cosW t, (1)

где W – циклическая частота источника напряжения.

Пусть U – напряжение на конденсаторе емкостью С, I – ток в контуре. Полагаем, что ток в КК квазистационарен (мгновенные значения тока одинаковы на всех участках цепи) и для мгновенных значений токов и напряжений выполняются законы, установленные для цепей постоянного тока. В любой момент времени сумма падений напряжений на всех элементах равна ЭДС источника:

U_L + IR + U = Е ₀cosW t. (2)

Падение напряжения на катушке индуктивности L:

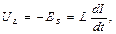(3)

ток в катушке и контуре:

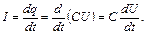(4)

Подстановка (3) и (4) в (2) приводит к выражению:

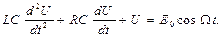(5)

Разделим это уравнение на LC и введем обозначения:

.

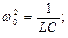
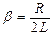Обозначая дифференцирование по времени точкой, получим дифференциальное уравнение:

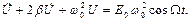(6)

Решение этого уравнения дает закон изменения напряжения на конденсаторе с течением времени и равно сумме полного решения однородного уравнения (7) и частного решения уравнения (6):

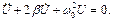(7)

Однородное уравнение (7) имеет решение:

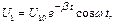(8)

являющееся уравнением затухающих колебаний.

Затухание определяется членом е^{-b t}. За время t = 1 /b амплитуда колебаний уменьшается в е раз. Затухание в КК связано с превращением энергии колебаний в теплоту на активной составляющей сопротивления контура R. При t >> 1 /b составляющая U ₁ решения уравнения (6) исчезнет, следовательно, она отражает переходный процесс, определенный начальными условиями и параметрами контура. Установившиеся колебания в цепи происходят с частотой W и возможным сдвигом по фазе. Поэтому решение ищут в виде:

U = U ₀ cos (W t + j), (9)

где U ₀ и j подлежат определению. Подстановка (9) в (6) дает:

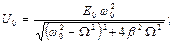(10)

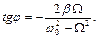(11)

Таким образом, амплитуда и фаза напряжения на конденсаторе зависят от соотношения частоты W источника ЭДС и частоты w ₀.

Ток в контуре:

,

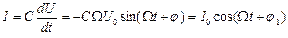где j ₁ = j + p /2. Амплитуда тока в контуре также зависит от соотношения частот W и w ₀:

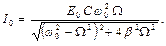(12)

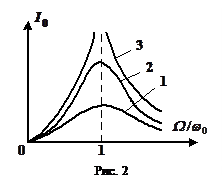
График зависимости I ₀ от W / w ₀ представлен на рис. 2. Из графика видно, что амплитуда тока резко возрастает при приближении циклической частоты W источника ЭДС к частоте w ₀. Это явление называется резонансом, а кривые – резонансными кривыми. Величина максимума тока I _{0 MAX} в контуре зависит от b: при b ® 0 Þ I _{0 MAX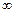} ® (кривая 3); при увеличении b максимальное значение I _{0 MAX} уменьшается (кривые 2 и 1), j ₁ определяет разность фаз колебаний тока в контуре и внешней ЭДС:

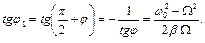(13)

График зависимости j ₁ от частоты представлен на рис. 3. Кривые 1 и 2 соответствуют разным значениям b (для кривой 2 величина b меньше, чем для кривой 1). При W = w ₀ Þ tg j ₁ = 0 и j ₁ = 0.

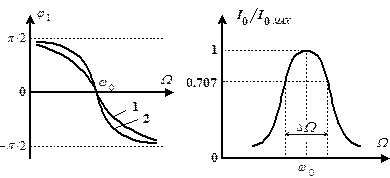
Рис. 3

Рис. 4

Для того, чтобы охарактеризовать избирательность колебательного контура по частоте вводится величина добротности КК:

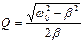. (14)

За редким исключением ширину резонансной кривой (полосу пропускания) принято определять по уровню 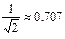(рис. 4).

Из формулы (12) следует, что максимальное значение тока 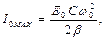тогда (12) можно переписать в виде:

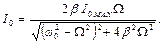(15)

Для нахождения полосы пропускания КК подставим в (15) значение :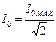

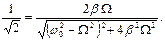(16)

Выражение (16) можно преобразовать к виду:

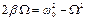или .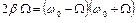

Учитывая, что w ₀ ‑ W = D W/2 и полагая, что вблизи резонанса w ₀ + W = 2W, получим: D W = 2 b. Отсюда:

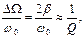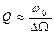т.е. (17)

Таким образом, относительная ширина резонансной кривой численно равна величине обратной добротности контура.

Для случая малого затухания (b << w ₀) формулу (14) можно переписать в следующем виде:

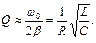(18)

ОПИСАНИЕ УСТАНОВКИ

Блок-принципиальная схема установки для изучения резонанса в последовательном колебательном контуре представлена на рис. 5.

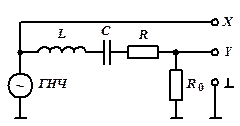
Рис. 5

Исследуемая цепь запитывается синусоидальным напряжением от генератора низких частот ГНЧ. На вход вертикального отклонения луча осциллографа подаётся снимаемое с сопротивления R ₀ напряжение, пропорциональное току в контуре. Элементами с изменяемыми номиналами являются С и R. Сопротивление R ₀, помимо своего прямого назначения, служит также для ограничения тока в цепи при R = 0. В режиме исследования фазовых кривых на горизонтальную развёртку осциллографа подаётся исходное напряжение ГНЧ.

Конструктивно элементы R и С выполнены в виде магазинов, позволяющих оперативно изменять номиналы этих элементов в процессе работы установки, при этом отклонения от выставленных номиналов не превышают 5 %. Элементы L и R ₀ выполнены в виде кассеты ФПЭ-11. В качестве ГНЧ используется звуковой генератор. Для наблюдения исследуемых процессов можно использовать любой низкочастотный осциллограф.

Дата добавления: 2015-05-06