Нормальный закон распределения

ПОНЯТИЕ О НОРМАЛЬНОМ ЗАКОНЕ РАСПРЕДЕЛЕНИЯ 135

параметров — оо«<а<Соо и а>0 является плотностью распреде­ления.

График интегральной функции распределения показан на рис. 30.

Из (4.1.1) и рис. 29 видно, что нормальное распределение сим­метрично относительно ординаты, отвечающей значению а;, равному а. Это значение является поэтому центром группирования (матема­тическим ожиданием) распределения. Если изменять а, то кривая у — п (х; а; а) будет перемещаться вдоль оси х, сохраняя свою форму. С возрастанием абсолютной величины уклонения (х — а), т. е. по мере удаления точки х от точки а, ордината кривой п (х-, а; о) быстро убывает; наибольшая ордината, отвечающая значению х=а,

имеет величину. — — = я(а; а; а). Эта ордината и является осью У 2л о

симметрии кривой. При а = 0 имеем семейство центрированных (т. е. с центром в начале координат) нормальных кривых

-—

*°' = п(хг, 0; а), (4.1.5)

зависящих от одного параметра а.

Когда параметр а уменьшается, начальная ордината кривой растет. Подъем кривой в центральной части компенсируется более резким спадом ее к оси х, так что общая величина площади, как мы видели, остается неизменной и равной единице. При очень малых значениях а кривая становится похожей на тонкую иглу, направленную вдоль оси у. Почти вся площадь под кривой сконцентрирована на неболь­шом интервале с центром в нуле. При возрастании а, наоборот, происходит «сплющивание» кривой, принимающей все более плоско-вершинную форму (рис. 31).

Чаще всего, однако, рассматривая величину, подчиненную нор­мальному закону N(x•, а; а), переходят к нормированному распре­делению. Нормирование распределения, вообще говоря, заключается в переходе от величины X к вспомогательной линейной функции

для которой

(4.1.6)

При нормальном распределении из (4.1.6) и (4.1.2) будем иметь:

«+» (ц-а)'

Р (Л < а + га) = N (а + га; а; а) = • -_ е~ *°° аи,

2яа

|А2яа.

. —во

[ГЛ. IV

откуда (заменяя переменное интеграции и на новое v, пользуясь

подстановкой

г>==— — - ""и й?г> = —) о;-.... 0 }

получим:

(4.1.7)

Дифференцируя (4.1.7) по верхнему пределу, получим:

; 0;

__

(4.1.8)

Таким образом, если произвести нормирование распределения п(х; а; а),.т* е. осуществить переход от величины X;,«..величине 2,

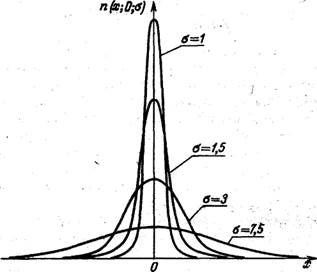
Рис. 31. Семейство «центрированных» нормальных кривых распределения 0=1; 1,5; 3; 7,5.

то плотность вероятности 2 выразится равенством (4.1.8), в котором уже отсутствуют параметры а и а. Все вопросы; связанные с нор­мальным распределением величины X, решают, переходя к вспомо­гательной величине 2., т. е. нормируя это распределение.

Нормирование распределения, как нетрудно понять, ведет-проста, к перенесению начала координат в центр группирования, т. «.-к «центрированию» и к выражению абсциссы в долях а, которое, как мы дальше увидим, представляет среднее квадратическое откло­нение величины X, т. е. а = а_х.

§ 11

Дата добавления: 2015-05-06