Понятие о нормальном законе распределения

ПОНЯТИЕ О НОРМАЛЬНОМ ЗАКОНЕ РАСПРЕДЕЛЕНИЯ

Ординаты кривой (4.1.8) табулированы. В таблице I приложений приведены значения этих ординат для значений г от 0 до 4,99. Эта таблица используется, в частности, для построения теоретической кривой распределения, когда эмпирическое распределение непрерыв­ной величины хотят глазомерно сравнить с нормальным распреде­лением.

Пусть, например, мы хотим провести такое сравнение распре­деления, приведенного в таблице 3.2.6. Мы приближенно определяем неизвестные нам параметры а и 0 нормального распределения по опытным данным: параметр а мы приравниваем средней арифмети­ческой отклонений размеров

а а? х ==4-4,3 мк:

и параметр |р?-нри$шш1иваем среднему квадратическому отклонению эмпирического распределения

0?*** I/ с —— 07 */*/• /**^ У О — С7 | I и/ТУП?

{эмпирические характеристики нами были подсчитаны в п. 3.2.4). Законность подобного приближенного определения параметров нами будет оправдана далее. Таким образом, мы получили нормаль­ную плотность в виде

п(х; 4,3; 9,7) =

/2я9,7 * ЛИГ"

Пронормируем это распределение. Для этого ширину интервалов выразим в долях о* и получим, что при Ах = 5 мк и 0=9,7 мк ширина &г в долях а равна

•:• ^; ' • ' ' '•••••' ^: " а ' &Х 5

Перенеся начало координате точку х= -\-4,3 мк, получим абсциссу середины первого интервала в долях 0 в виде

г — **—^й _ —17,5—4,3 _ ₉ „ ^г1—5-~ д^—~"^*,ш.

Учитывая, что Аг;==0,515, далее получим:

г_ъ = — 2,247 + 0,515 = -^ 1,732, ^ = —1,7324:0,515 = —1,517,;

,и т. д. (см. строку 2 таблицы 4.1.1).

Для этих точек мы находим по таблице I приложений I значения йлоуйости (4.1.8) для величины 2, проставленные в строке 3 таблицы 4.1.1.

Помножая эти величины на ширину интервала Аг, найдем при­ближенную величину площади под кривой в каждом интервале,

§ И

характеризующей вероятность попадания в него. Ее естественно сопоставить с наблюденными в выборке частостями чи (^/приведен­ными в строке 5 таблицы 4.1.1, для чего последние можно пред­ставить в виде площадей прямоугольников, построенных на интер­валах. Тогда, очевидно, ординаты этих прямоугольников будут равны

-г-^ (см. строку 6 таблицы 4.1.1). Пользуясь последними, мы строим

гистограмму распределения, а через точки, отвечающие плотностям р(г), проводим соответствующую нашей гистограмме нормальную кривую распределения (рис. 32).

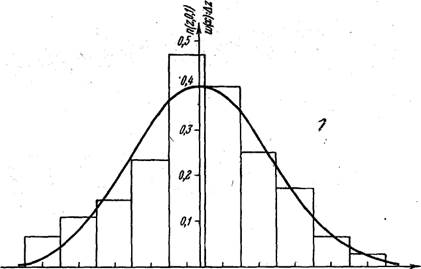
-1&7 -0,702 -Ц1870 +Ш +0.8Я +1,358 +1,873 +2,388 г

Рис. 32. Гистограмма распределения 200 валиков по диаметрам,

совмещенная с графиком нормальной плотности вероятности

п (г; 0; 1) при «=^# = 4,3 мк и а = 5 = 9,7 мк.

Мы видим, что гистограмма нормированного распределения, естественно, имеет такой же вид, как и гистограмма, показанная на рис. 27, только здесь по оси абсцисс отложены не микроны,

вместо отношений

а доли а и по оси ординат — отношения

• -< -, использованных при построении рис. 27.

Дата добавления: 2015-05-06