Погашение потребительского кредита

Начисление процентов в потребительском кредите обсуждалось в параграфе 1.5. Напомним, что проценты начисляются на всю сумму кредита в начале срока (разовое начисление процентов). Расходы по обслуживанию долга в этом случае определяются как:

, (8.12)

где S — наращенная сумма долга, см. формулу (1.1);

n — срок кредита в годах;

т — количество выплат в году (обычно m = 12).

Рассмотрим проблему определения остатка задолженности на любой промежуточный момент времени срока кредита. Необходимость в этом возникает, например, при досрочном погашении долга. Для решения этой задачи следует разбить величину R на проценты и сумму, идущую на погашение основного долга. За рубежом эта процедура часто основывается на весьма специфичном правиле 78 (Rule of 78) или методе сумм чисел (Sum of Digits). Нельзя исключать и другие методы. Например, представляется приемлемым равномерное распределение выплат процентов. Впрочем, для должника, если он предполагает погасить долг в оговоренный срок (но не ранее), не имеет значения, какой метод распределения процентов принят.

Обсуждение начнем с последнего, более простого метода. Нетрудно определить, что в этом случае деление расходов на постоянные суммы процентов и погасительные платежи достигается при

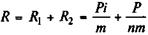, (8.13)

где P — сумма основного долга без процентов (цена товара);

R ₁ и R ₂ — проценты и размер погашения основного долга.

Перейдем к правилу 78. Сумма порядковых номеров месяцев в году равна 78, отсюда и название правила. Для начала допустим, что срок кредита равен году. Тогда согласно правилу 78 доля процентов в сумме расходов в первом месяце равна 12 / 78, во втором она составит 11 / 78 и т.д. Последняя уплата процентов равна 1 / 78. Таким образом, доля процентов линейно убывает. Иная картина наблюдается при погашении основного долга — сумма списания последовательно увеличивается. Для годового срока находим:

Обобщим это правило для кредита со сроком N месяцев. Последовательные номера месяцев в обратном порядке представляют собой числа t = N, N - 1,..., 1, а сумма этих чисел находится как

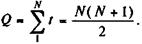
Доли от общей суммы начисленных процентов находятся как t/Q. Отсюда

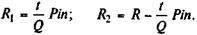(8.14) (8.15)

Таким образом, в каждом месяце выплаты процентов сокращаются на величину Pin/Q, на такую же сумму увеличиваются суммы списания основного долга.

Пример 8.5. Потребительский кредит в сумме 10 млн. руб. выдан на три года при разовом начислении процентов по ставке 10% годовых.Погашение задолженности помесячное. Общая сумма задолженности

S = 10 000(1 + 3 х 0,1) = 13 000 тыс.руб.

Сумма расходов по обслуживанию долга

R = 13 000 / 36 =361,111 тыс. руб.

Сумма номеров месяцев

Q = = 666; t = 36; 35;...,1.

Для первого месяца находим:

R ₁ = 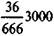= 162,162; R ₂ = 361,111 - 162,162 = 198,949 тыс. руб.

Если проценты и суммы погашения долга определять по формуле (8.13), то

R ₁ = = 83,333; R ₂ = = 277,778 тыс. руб.

В табл. 8. 3 приведены данные, характеризующиепроцесс погашения долга по правилу 78 — графы 2 - 4. Кроме того, для сравнения показана динамика остатка задолженности при равных суммах списания — графа 5.

Таблица 8.3

Месяц	Остаток долга на начало месяца	Проценты	Погашение долга	Остаток долга на начало месяца
	10000,00	162,16	198,95	10000,00
	9801,05	157,66	203,45	9722,22
	9597,60	153,15	207,96	9444,44
...
	6804,82	99,10	262,01	6111,11
	6542,81	94,59	266,52	5833,33
...
	708,70	9,01	352,10	555,55
	356,60	4,51	356,60	277,78
Итого

Как видим, размер процентов по правилу 78 ежемесячно сокращается на сумму, немного превышающую 4,5 тыс. руб. (за весь срок с 162,16 до 4,51), соответственно увеличиваются суммы списания. Такую схему начисления процентов можно трактовать и как применение переменной месячной процентной ставки (от 16,22 до 0,45%), начисляемой на первоначальную сумму долга. Второй вариант (равномерное списание) приводит к более быстрому списанию задолженности. Так, за первые 15 месяцев по правилу 78 списывается 34,5% долга, по альтернативному варианту — 41,7%.

Важно отметить, что впотребительском кредите при разовом начислении процентов должник фактически выплачиваетпроценты и за списанные суммы долга. Иначе говоря, если бы проценты начислялись на остатки долга, то кредит обошелся бы заметно дешевле (при той же процентной ставке). Так, пусть в последнем примере погашение задолженности производится по схеме "равныесрочные уплаты" (см. параграф 7.3). Тогда согласно формуле (7.10) получим:

R = 10 000 /a _36;0,8333 = 322,67 тыс. руб.

Это заметно ниже полученнойв примере 8.5 суммы расходов.

Глава 9. АНАЛИЗ КРЕДИТНЫХ ОПЕРАЦИЙ

Дата добавления: 2015-03-31