Часть В

1. Сформулируйте теорему Абеля для степенных рядов. Может ли ряд , расходящийся в точке , сходиться при ?

Если степенной ряд a₀+a₁x+a₂x+…+a_nx_n+… сходится при некотором х=х₀, не равном нулю, то он сходится, и притом абсолютно, при всех х, удовлетворяющих условию |х|<|x₀|; Если ряд a₀+a₁x+a₂x+…+a_nx_n+… расходится при некотором х=х₁, то он расходится при всех х, удовлетворяющих условию |х|>|x₁|

Данный ряд, расходящийся в точке -2 не может сходиться при х=3, т.к. |-2|<|3| следовательно согласно теореме Абеля ряд в точке х = 3 сходится, и притом абсолютно.

2. Сформулируйте теорему о почленном дифференцировании степенного ряда. Используя эту теорему, найдите сумму ряда при .

Теорема о почленном дифференцировании степенного ряда: пусть функция f(x) разлагается на интервале (-R,R) в степенной ряд: f(x) = a₀+a₁x+a₂x²+…+a_nxⁿ+…(1). Рассмотрим степенной ряд: a₁+2a₂x+…+na_nx^n-1+…(2), полученный почленным дифференцированием ряда (1). Тогда:

1. ряд (2) имеет тот же радиус сходимости R, что и ряд (1).

2. на всем интервале (-R,R) функция f(x) имеет производную f^,(x), которая разлагается в степенной ряд (2).

∑nxⁿ=x∑nx^n-1=x∑(xⁿ)’=x/(1-x)²

∑xⁿ=x/(1-x) |x|<1 – сходится

∑nx^n-1=(x/1-x)’=(1-x+x)/1/(1-x)²

3. Сформулируйте достаточное условие разложимости функции в ряд Маклорена. Докажите, что функция разлагается в ряд Маклорена на любом интервале .

Достаточное условие разложения функции в ряд Маклорена: пусть функция f(x) определена и бесконечно дифференцируема на интервале (-R,R). Если существует такая постоянная: M=const для любого х (-R, R) <M, n=0,1,2,…, то в этом интервале ряд Маклорена сводится к функции f(x). Имеем: (sinx)’=cosx; (sinx)’’=-sinx, (sinx)’’’=-cosx, (sinx)⁽⁴⁾=sinx. Отсюда видно, что последовательность производных функции sinx периодична с периодом 4. При х=0 получаем sin0=0, sin’(0)=1, sin’’(0)=0, sin’’’(0)=-1 В общем случае все производные четного порядка равны 0, а нечетного sin^(2т+1)(0)=(-1)ⁿОтсюда ряд Маклорена для sinx:Sinx=x-(x³/3!)+(x⁵/5!)-…+(1)ⁿ(x²ⁿ⁺¹/(2n+1)!)+…

4. Сформулируйте достаточное условие разложимости функции в ряд Маклорена. Докажите, что функция 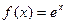разлагается в ряд Маклорена на всей числовой оси.

Достаточное условие разложения функции в ряд Маклорена: пусть функция f(x) определена и бесконечно дифференцируема на интервале (-R,R). Если существует такая постоянная: M=const для любого х (-R, R) <M, n=0,1,2,…, то в этом интервале ряд Маклорена сводится к функции f(x). Пусть f(x)=e^x. В любом интервале (-r;r) имеем |f⁽ⁿ⁾(x)|= e^x<e^r. В силу признака Даламбера отсюда следует, что функция е^ч равна сумме своего ряда Маклорена при хϵ(-r;r), а значит, и для любого х ввиду произвольности r. Поскольку f⁽ⁿ⁾(0)=e⁰=1 при любом n, получаем разложение e^x=1+x+(x²/2!)+(x³/3!)+…+(xⁿ/n!)+… справедливо для всех х.

5. Сформулируйте теорему о почленном дифференцировании степенного ряда. Используя эту теорему, найдите разложение функции в ряд Маклорена, исходя из разложения функции .

Теорема о почленном дифференцировании степенного ряда: пусть функция f(x) разлагается на интервале (-R,R) в степенной ряд: f(x) = a₀+a₁x+a₂x²+…+a_nxⁿ+…(1). Рассмотрим степенной ряд: a₁+2a₂x+…+na_nx^n-1+…(2), полученный почленным дифференцированием ряда (1). Тогда:

1. ряд (2) имеет тот же радиус сходимости R, что и ряд (1).

2. на всем интервале (-R,R) функция f(x) имеет производную f^,(x), которая разлагается в степенной ряд (2)

ряд для cosx получается почленным дифференцированием ряда Sinx=x-(x³/3!)+(x⁵/5!)-…+(-1)ⁿ(x²ⁿ⁺¹/(2n+1)!)+…

(Sinx)’=x’-(x³/3!)’+(x⁵/5!)’-…+((-1)ⁿ(x²ⁿ⁺¹/(2n+1)!))’+…

Cosx=1-x²/2!+x⁴/4!-…+(-1)ⁿ(x²ⁿ/(2n!)

6.

7.

8.

9.

10.

11. Найти значение а, при котором функция 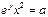является решением дифференциального уравнения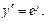

12.

13. Сформулируйте теорему существования и единственности решения задачи Коши для дифференциального уравнения первого порядка Проверьте выполнение условий этой теоремы для задачи ,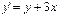

Если в некоторой окрестности точки (х₀;у₀) функция f(x,y) определенная, непрерывна и имеет непрерывную частную производную f’_y, то существует такая окрестность точки (х₀;у₀), в которой задача Коши y’=f(x,y), y(x₀)=y₀имеет решение, притом единственное.

Подставим в исходное:

Запишем общее решение:

Подставим значения условий для задачи Коши

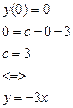
Ответ: с=3 и у= -3х.

14. Какое решение дифференциального уравнения называется особым? Найдите особое решение уравнения .

Особое решение дифференциального уравнения – это некоторая интегральная прямая уравнения, состоящая из особых точек.

Практика:

Решение уравнения, но есть особые решения при y(x)=0.

15. Дайте определение и приведите пример дифференциального уравнения с разделяющимися переменными. Приведите уравнение 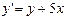к виду уравнения с разделенными переменными. Одним из наиболее простых, но весьма важных типов дифференциальных уравнений являются уравнения с разделяющимися переменными. Это дифференциальные уравнения вида: y’=f(x)g(y), где f(x) и g(y) – непрерывные функции.

Проверим на однородность функцию:

=> однородны.

Уравнение с разделяющимися переменными.

Дата добавления: 2015-03-29