Ввод ограничений

Курсор в поле Добавить. Появится диалоговое окно Добавление ограничения (Рисунок 16.).

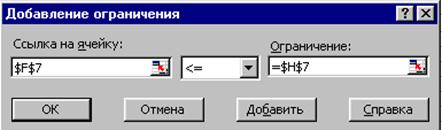
Рисунок 16. Ввод правых и левых частей ограничений.

· В окне Ссылка на ячейку ввести $F$7.

· Ввести знак ограничение £..

· Курсор в правое окно.

·Вести $H$7.

· Добавить. На экране опять диалоговое окно Добавление ограничения. Ввести остальные ограничения.

· После ввода последнего ограничения ввести ОК.

На экране появится диалоговое окно Поиск решения с введенными условиями (Рисунок 17).

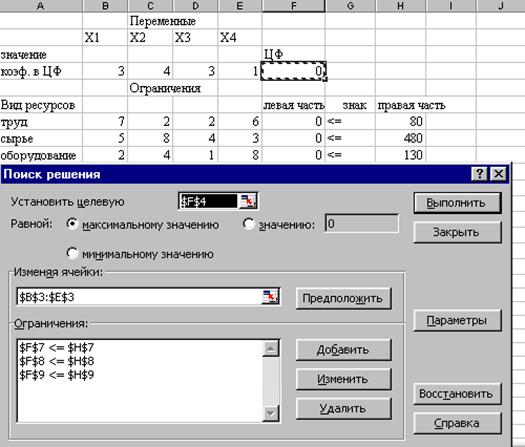
Рисунок 17. Введены все условия для решения задачи.

8) Ввод параметров для решения ЗЛП (Рисунок 18).

§ Открыть окно Параметры поиска решения.

§ Установить флажок Линейная модель, что обеспечивает применение симплекс-метода.

§ Установить флажок Неотрицательные значения.

§ ОК (На экране диалоговое окно поиска решения).

§ Выполнить (На экране диалоговое окно результаты поиска решения – Рисунок 19. ).

Рисунок 18. Ввод параметров.

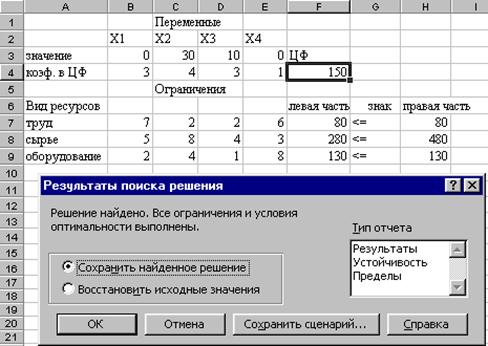
Рисунок 19. Решение найдено.

Полученное решение означает, что максимальный доход 150 тыс. руб. фабрика может получить при выпуске 30 ковров второго вида и 10 ковров третьего вида. При этом ресурсы труд и оборудование будут использованы полностью, а из 480 кг пряжи (ресурс сырье) будет использовано 280 кг.

Создание отчета по результатам поиска решения

Excel позволяет представить результаты поиска решения в форме отчёта. Существует три типа таких отчетов:

§ Результаты (Answer). В отчет включаются исходные и конечные значения целевой и влияющих ячеек, дополнительные сведения об ограничениях

§ Устойчивость (Sensitivity). Отчет, содержащий сведения о чувствительно­сти решения к малым изменениям в изменяемых ячейках иди в формулах ограничений.

§ Пределы (Limits). Помимо исходных и конечных значений изменяемых и целевой ячеек в отчет включаются верхние и нижние границы значений, которые могут принимать влияющие ячейки при соблюдении ограничений.

1. Отчет по результатам.

Отчет по результатам
Целевая ячейка (Максимум)
	Ячейка	Имя	Исходно	Результат
	$F$4	коэф. в ЦФ ЦФ
Изменяемые ячейки
	Ячейка	Имя	Исходно	Результат
	$B$3	значение Х1
	$C$3	значение Х2
	$D$3	значение Х3
	$E$3	значение Х4
Ограничения
	Ячейка	Имя	Значение	Формула
	$F$7	труд левая часть		$F$7<=$H$7
	$F$8	сырье левая часть		$F$8<=$H$8
	$F$9	оборудование левая часть		$F$9<=$H$9

В отчете по результатам содержатся оптимальные значения переменных Х₁, Х₂, Х₃, Х₄ , которые соответственно равны 0,10, 30,0; значение целевой функции – 150, а также левые части ограничений.

Двойственность в задачах линейного программирования. Анализ полученных оптимальных решений.

С каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной; первоначальная задача называется исходной или прямой.

Связь исходной и двойственной задач заключается, в част­ности, в том, что решение одной из них может быть получено непосредственно из решения другой.

Переменные двойственной задачи y_i называют объективно обусловленными оценками, или двойственными оцен­ками, или «ценами» ресурсов, или теневыми ценами.

Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой.

Двойственная задача по отношению к исходной состав­ляется согласно следующим правилам:

1) целевая функция исходной задачи формули­руется на максимум, а целевая функция двойственной задачи— на минимум, при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид £, в задаче на минимум — вид ³;

2) матрица А, составленная из коэффициентов при неизвестных в сис­теме ограничений исходной задачи и аналогич­ная матрица А^т в двойственной задаче получаются друг из друга транс­понированием;

3) число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений в системе двойственной задачи — числу переменных в исходной задаче;

4) коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи — коэффициенты при неизвестных в целевой функции исходной задачи;

5) каждому ограничению одной задачи соответствует переменная другой задачи: номер переменной совпадает с номером ограничения; при этом ограничению, записан­ному в виде неравенства £, соответствует переменная, связанная условием неотрицательности. Если функцио­нальное ограничение исходной задачи является равенст­вом, то соответствующая переменная двойственнвой; задачи может принимать как положительные, так и отрицательные значения

Модель исходной (прямой) задачи в общем виде может быть записана следующим образом:

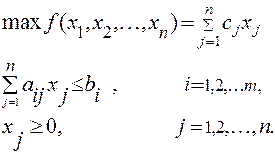
Модель двойственной задачи имеет вид:

Две приведенные задачи образуют пару симметричных двойственных задач. Основные утверждения о взаимно двойственных задачах содержатся в двух следующих теоремах.

Первая теорема двойственности.

Для взаимно двойственных задач имеет место один из взаимоисключающих случаев:

1. В прямой и двойственной задачах имеются оптимальные реше­ния, при этом значения целевых функций на оптимальных решениях совпадают: f(x) = g(y).

2. В прямой задаче допустимое множество не пусто, а целевая функция на этом множестве не ограниченна сверху. При этом у двойственной задачи будет пустое допустимое множество.

3. В двойственной задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым.

4.Обе из рассматриваемых задач имеют пустые допустимые множества.

Экономический смысл первой теоремы двойственности следующий. План производства Х и набор оценок ресурсов У оказываются оптимальными тогда и только тогда, когда прибыль от реализации продукции, определенная, при из­вестных заранее ценах продукции равна затра­там на ресурсы по «внутренним» (определяемым только из решения задачи) ценам ресурсов y_i. Для всех же других планов Х и У обеих задач прибыль от продукции всегда меньше (или равна) стоимости затраченных ресурсов:

f(X) < g(Y}, т. е. ценность всей выпущенной продукции не превосходит суммарной оценки имеющихся ресурсов. Зна­чит величина g(Y) - f(X) характеризует производственные потери в зависимости от рассматриваемой производственной программы и выбранных Оценок ресурсов.

Из первой теоремы двойственности следует, что при оп­тимальной производственной программе и векторе оценок ресурсов производственные потери равны нулю.

Вторая теорема двойственности

(теорема о дополняющей нежесткости)

Пусть X=(x₁,x₂,...x_n) - допустимое решение прямой задачи, а Y= (y₁,y₂,...y_m) - допустимое решение двойственной задачи. Для того чтобы они были оптимальными решениями соответственно прямой и двойственной задач необходимо и достаточно, чтобы выполнялись следующие соотношения:

*

**

Условия (*) и (**) позволяют, зная оптимальное решение одной из взаимно двойственных задач, найти оптимальное решение другой задачи.

Из второй теоремы двойственности в данном случае следуют такие требования на оптимальную производственную программу X=(X₁,X₂,...,X_n) и оптимальный вектор оценок Y=(Y₁,Y₂,...,Y_m):

(4)

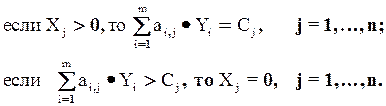(5)

Условия (4) можно интерпретировать так: если оценка yi единицы ресурса i-го вида положительна, то при оптимальной производственной программе этот ресурс используется полностью, если же ресурс используется не полностью, то его оценка равна нулю. Из условия (5) следует, что если j-й вид продукции вошел в оптимальный план, то он в оптимальных оценках неубыточен, если же j-й вид продукции убыточен, то он не войдет в план, не будет вы­пускаться.

Рассмотрим еще одну теорему, выводы которой будут использованы в дальнейшем.

Теорема об оценках.

Значения переменных Y_i в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов bi системы ограничений-неравенств прямой задачи на величину

Решая ЗЛП симплексным методом, мы одновременно решаем двойственную ЗЛП. Переменные двойственной задачи yi называют объективно обусловленными оценками.

Рассмотрим экономическую интерпретацию двойственной задачи на примере задачи оптимального использования ресурсов.

Пример. Сформулируем экономико-математическую модель двойственной задачи к задаче о коврах.

Прямая задача:

f(x) = 3Х₁ +4Х₂ +3Х₃ +1Х₄

Ограничения по ресурсам

7Х₁ +2Х₂ +2Х₃ +6Х₄ 80

5Х₁ +8Х₂ +4Х₃ +3Х₄ 480

2Х₁ +4Х₂ +Х₃ +8Х₄ 130

Х₁, Х₂, Х₃, Х₄ 0

Количество неизвестных в двойственной задаче равно числу функциональных ограничений в исходной задаче. В исходной задаче три ограничения – по труду, по сырью и по оборудованию. Следовательно, в двойственной задаче – три неизвестных:

Y₁ – двойственная оценка ресурса труд, или «цена» труда;

Y₂ – двойственная оценка ресурса сырье, или «цена» сырья;

Y₃ – двойственная оценка ресурса оборудование, или «цена» оборудования.

Целевая функция двойственной задачи формулируется на минимум. коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи.

g = 80 ´Y₁ + 480´Y₂ + 130´Y₃ ® min

Необходимо найти такие “цены” на ресурсы (Y_i), чтобы общая стоимость используемых ресурсов была минимальной.

Ограничения. число ограничений в системе двойственной задачи равно числу переменных в исходной задаче. В исходной задаче четыре переменных, следовательно, в двойственной задаче четыре ограничения. правыми частями в ограничениях двойственной задачи являются коэффициенты при неизвестных в целевой функции исходной задачи. Левая часть ограничения определяет стоимость ресурсов, затраченных на производство единицы продукции. Каждое ограничение соответствует определенному виду продукции.

7 ´Y₁ + 5 ´Y₂ + 2 ´Y₃ ³ 3

2 ´Y₁ + 8´Y₂ + 4´Y₃ ³ 4

2 ´Y₁ + 4´Y₂ + 1´Y₃ ³ 3

6 ´Y₁ + 3´Y₂ + 8´Y₃ ³ 1

Y₁ ,Y₂ ,Y₃ ³ 0

Решение двойственной задачи можно найти в отчете Поиска решений. Отчет по устойчивости. Теневые цены ресурсов труд, сырье и оборудование соответственно равны 4/3, 0, 1/3 или в десятичных дробях 1.3333, 0, 0.3333.

Отчет по устойчивости
Изменяемые ячейки
			Результ.	Нормир.	Целевой	Допустимое	Допустимое
	Ячейка	Имя	Значение	Стоимость	Коэффициент	Увеличение	Уменьшение
	$B$3	Значение Х1		-7			1E+30
	$C$3	Значение Х2
	$D$3	Значение Х3					1.75
	$E$3	Значение Х4		-9.667		9.667	1E+30
Ограничения
			Результ.	Теневая	Ограничение	Допустимое	Допустимое
	Ячейка	Имя	Значение	Цена	Правая часть	Увеличение	Уменьшение
	$F$7	труд левая часть		1.333
	$F$8	сырье левая часть				1E+30
	$F$9	Оборудование левая часть		0.333

Проведем анализ полученного оптимального решения исходной задачи с помощью двойственных оценок.

1) Анализ использования ресурсов в оптимальном плане выполняется с помощью соотношений второй теоремы двойственности.

Ресурсы труд и оборудование имеют отличные от нуля оценки 4/3 и 1/3 – эти ресурсы полностью используются в оптимальном плане, являются дефицитными, сдерживающими рост целевой функции. Правые части этих ограничений равны левым частям.

7Х₁ +2Х₂ +2Х₃ +6Х₄ 80

2Х₁ +4Х₂ +Х₃ +8Х₄ 130

7´0 +2´30 +2´10 +6´0= 80=80

2´0 +4´30 +1´10 +8´0= 130=130

Ресурс сырье используется не полностью (280<480), поэтому имеет нулевую двойственную оценку (Y2=0).

5Х₁ +8Х₂ +4Х₃ +3Х₄ 480

5´0 +8´30 +4´10 +3´0= 280<480

Этот ресурс не влияет на план выпуска продукции.

Общая стоимость используемых ресурсов при выпуске 30 ковров второго вида и 10 ковров третьего вида составит 150 тыс. руб.

g = 80 ´Y1 + 480´Y2 + 130´Y3 =80 ´4/3 +480´0+130´1/3 =150 тыс. руб.

По условию (4) не использованный полностью в оптимальном плане ресурс по­лучает нулевую оценку. Нулевая оценка ресурса свидетель­ствует о его не дефицитности. Ресурс не дефицитен не из-за его неограниченных запасов (они ограничены величиной bi), а из-за невозможности его полного использования в опти­мальном плане. Так как суммарный расход недефицитного ресурса меньше его общего количества, то план производст­ва им не лимитируется. Данный ресурс не препятствует и дальше максимизировать целевую функцию f(X).

Заметим, что ценность различных видов ресурсов нельзя отождествлять с действительными ценами, по которым осуществляется его закупка. В данном случае речь идет о некоторой мере, имеющей экономическую природу, которая характеризует ценность ресурса только относительно полу­ченного оптимального решения.

2) Анализ эффективности отдельных вариантов плана выполняется на основе соотношений из 2 теоремы двойственности.

Если изделие вошло в оптимальный план (Xj >0), то в двойственных оценках оно не убыточно, то есть, стоимость ресурсов, затраченных на производство единицы изделия равна его цене. Такие изделия эффективны, выгодны с точки зрения принятого критерия оптимальности. В нашей задаче это ковры второго и третьего видов.

Если стоимость ресурсов, затраченных на производство одного изделия больше его цены, то это изделие не войдет в оптимальный план из-за его убыточности. В нашей задаче в план выпуска не вошли ковры первого и четвертого видов, потому что затраты по ним превышают цену на 7 (10-3) тыс. руб. и 9.666 (10.666-1) тыс. руб. соответственно. Это можно подтвердить, подставив в ограничения двойственной задачи оптимальные значения вектора Y.

7 ´4/3 + 5´0+ 2´1/3=30/3= 10 >3

2 ´4/3 + 8´0+ 4´1/3=12/3= 4= 4

2 ´4/3 + 4´0+ 1´1/3= 9/3= 3= 3

6´4/3 + 3´0+ 8´1/3=32/3= 10.666 > 1

Разницу между правыми и левыми частями ограничений двойственной задачи можно найти в Отчете по устойчивости в столбце Нормируемая стоимость.

2) Анализ влияния изменения правых частей ограничений на значения целевой функции (Чувствительность решения к изменению запасов сырья).

Предположим, что запас сырья ресурса «труд» изменился на 12 единиц, т. е. теперь он составляет 80 + 12 = 92 единиц. Из теоремы об оценках, известно, что колеба­ние величины b_i приводит к увеличению или уменьшению f(X). Оно определяется величиной y_i в случае, когда при изменении величин b_i значения переменных y_i в оптималь­ном плане соответствующей двойственной задачи остаются неизменными. В нашей задаче увеличение запасов ресурса «труд» приведет к увеличению значения целевой функции на 16 тыс. руб.(Df(x)= Db₁´ y₁ =12 ´ 4/3 = 16 ). Для двойственных оценок оптимального плана весьма существенное значение имеет их предельный характер. Точной мерой влияния ограничений на функционал оцен­ки являются лишь при малом приращении ограничения. Известно, что оценки не меняют своей величины, если не меняется набор векторов, входящих в базис оптимального плана, тогда как интенсивность этих векторов (значения неиз­вестных) в плане могут меняться.

Поэтому необходимо знать такие интервалы изменения каждого из свободных членов системы ограниче­ний исходной ЗЛП, или интервалы устойчивости двойственных оценок, в которых оптимальный план двойст­венной задачи не менялся бы. Эту информацию можно получить из Отчета по устойчивости. В нашей задаче в ниже приведенном фрагменте отчета видно, что запасы дефицитных ресурсов труд и оборудование могут быть, как уменьшены, так и увеличены, увеличение запаса ресурса сырье не повлияет на план выпуска продукции.

Ограничение	Допустимое	Допустимое
правая часть	Увеличение	уменьшение
	1E+30

После увеличения запаса ресурса труд до 92 чел/ часов было получено новое решение задачи. Изменение запасов ресурсов в пределах интервалов устойчивости двойственных оценок привело не только к изменению значения целевой функции на 16 тыс. руб., но и к изменению плана выпуска. При этом структура плана не изменилась - изделия, которые были убыточны не вошли и в новый план выпуска, т.к. цены на ресурсы не изменились. Новый план выпуска составляет 28 ковров второго вида и 18 ковров третьего вида. Изменение общей стоимости продукции на 16 тыс. руб. (24-8=16) получено за счет уменьшения на 2 единицы ковров второго вида по цене 4 тыс. руб. (4 тыс. руб.´(28-30)= -8 тыс. руб.) и увеличения на 8 единиц ковров третьего вида по цене 3 тыс. руб. (3 тыс. руб.´(18-10)= 24 тыс. руб.).

Отчет по устойчивости 2
Изменяемые ячейки
			Результ.	Нормир.	Целевой	Допустимое	Допустимое
	Ячейка	Имя	значение	Стоимость	коэффициент	увеличение	уменьшение
	$B$3	значение Х1		-7			1E+30
	$C$3	значение Х2
	$D$3	значение Х3					1.75
	$E$3	значение Х4		-9.667		9.667	1E+30
Ограничения
			Результ.	Теневая	Ограничение	Допустимое	Допустимое
	Ячейка	Имя	значение	цена	правая часть	увеличение	уменьшение
	$F$7	труд левая часть		1.333
	$F$8	сырье левая часть				1E+30
	$F$9	оборудование левая часть		0.333

Задача 5.

Задача о размещении производственных заказов

в планируемом периоде необходимо обеспечить производство 300 тыс. однородных новых изделий, которые могут выпускаться на четырех филиалах предприятия. Для освоения этого нового вида изделий выделены капитальные вложения в размере 18 млн. руб.. Разработанные для каждого филиала предприятия проекты освоения нового вида изделия характеризуются величинами удельных капитальных вложений и себестоимостью единицы продукции в соответствии с таблицей.

Необходимо найти такой вариант распределения объемов производства продукции и ка­питальных вложений по филиалам, при котором суммарная стоимость изделий будет минимальной.

Таблица

Показатель	Филиал предприятия
Себестоимость производства изделия, руб.
Удельные капиталовложения, руб.

В результате решения получен план распределения объемов производства по филиалам предприятия

Филиал предприятия
	100 тыс. штук	200 тыс. штук

Требуется:

1) Сформулировать экономико-математическую модель прямой и двойственной задачи.

2) Найти оптимальный план двойственной задачи, используя теоремы двойственности.

Дата добавления: 2015-03-31