Решение. 1) Экономико-математическая модель исходной задачи

1) Экономико-математическая модель исходной задачи.

X_i - объем выпускаемой продукции на i-м филиале предприятия.

= 83X₁+89X₂+95X₃+98X₄ -> min,

Ограничения

X₁+X₂+X₃+X₄ ³ 300 (тыс. штук)

120X₁+80X₂+50X₃+40X₄ £ 18 (млн.руб.),

X_1,2,3,4 ³ 0.

Y1
Y2

Экономико-математическая модель двойственной задачи.

Y₁ - двойственная оценка выпускаемой продукции, которая может быть ценой изделия;

Y₂ - двойственная оценка капитальных вложений, которая может быть представлена как коэффициент эффективности капитальных вложений.

g = 300000 Y₁₊18000000 Y₂ -> mах

1 Y₁+120Y₂ £ 83

1 Y₁+ 80Y₂ £ 89

1 Y₁+ 50Y₂ £ 95

1 Y₁+ 40Y₂ £ 98

2) для определения оптимального плана двойственной задачи воспользуемся соотношениями второй теоремы двойственности. Если какое-либо ограничение исходной задачи выполняется как строгое неравенство, то соответствующая двойственная оценка равна нулю

().

0+100000+200000+0 = 300000

120´0+80´100000+50´200000+4´0 = 18000000

Если какая-либо переменная исходной задачи входит в оптимальный план, то соответствующее ограничение двойственной задачи выполняется как строгое равенство

).

В нашей задаче Х2 =100000>0 и Х3 =200000>0, поэтому второе и третье ограничения двойственной задачи обращаются в уравнения, решая которые найдем Y1и Y2.

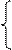
1 Y₁+ 50Y₂ = 95 Y₁= 105 - средняя цена изделия

1 Y₁+ 80Y₂ = 89 Y₂ = - 0.2 - двойственная оценка капитальных вложений.

105 =95 +50´0.2 = 105

105 =89+ 80´0.2 = 105

На втором и третьем филиалах выпускать новые изделия целесообразно так как затраты на его освоение и выпуск не превышают цену изделия.

Проверим выполнение первой теоремы двойственности.

g = 300000 Y₁[phone] Y₂ = 300000 ´105₊18000000´(–0.2) = 279 000 000

= 83X₁+89X₂+95X₃+98X₄ =83´0+89´100000+95´200000+98´0 = 279 000 000.

Полученные оптимальные планы говорят о том, что в первом и четвертом филиалах размещать заказы по выпуску новых изделий невыгодно (Х1=0 и Х4=0), так как затраты на производство единицы изделия в этих филиалах больше цены изделия.

1 ´Y₁+ 120´Y₂ = 83 Y₁= 105 105+ 120´(-0.2) < 95 105< 95+24 = 119

1 ´Y₁+ 40´Y₂ = 98 Y₂ = - 0.2 105+ 40´(-0.2) < 89 105<98+8 = 106.

Задания к контрольной работе

Номер Вашего варианта соответствует последней цифре зачетной книжки.

ЗАДАЧА 1.

1. Решить графическим и симплексным методом задачу линейного программирования.

2. Сформулировать двойственную задачу и найти ее оптимальный план, используя теоремы двойственности.

Вариант 1

Max f (x) = 3X₁ + 2X₂

X₁ + 2X₂ ≤ 11

2X₁ - X₂ ≥ 5

X₁ + 3X₂ ≥ 14

X₁ , X₂ ≥ 0

Вариант 2

Max f (x) = 3X1 + 2X2

X1 + 2X2 ≤ 12

2X1 - X2 ≥ 7

X1 + 3X2 ≥ 14

X1, X2 ≥ 0

Вариант 3

Max f (x) = 3X1 + 2X2

X1 + 2X2 ≥ 10

2X1 - X2 ≤ 18

X1 + 3X2 ≤ 13

X1, X2 ≥ 0

Вариант 4

Min f (x) = 3X1 + 2X2

X1 + 2X2 ≥10

2X1 - X2 ≥ 10

X1 + 3X2 ≤ 13

X1, X2 ≥ 0

Вариант 5

Max f (x) = 4х1+ 3х2

х1 + 2х2 £ 10

х1 + 2х2 ³ 2

2х1 + х2 £ 10

х1 ³ 0, х2 ³ 0

Вариант 6

Min f (x) = 3X1 + 2X2

X1 + 2X2 ≥12

2X1 - X2 ≥ 12

X1 + 3X2 ≤ 14

X1, X2 ≥ 0

Вариант 7

Max f (x) = 3х1+ 5х2

х1 + х2 £ 5

3х1 + 2 х2 £ 8

х1 ³ 0, х2 ³ 0

Вариант 8

Min f (x) = 3X1 + 2X2

X1 + 2X2 ≤ 11

2X1 - X2 ≥ 5

X1 + 3X2 ≥ 14

X1, X2≥ 0

Вариант 9

Max f (x) = 3х1+ х2

2х1 + 3х2 ³ 12

-х1 + х2 £ 2

2х1 - х2 £ 2

х1 ³ 0, х2 ³ 0

Вариант 10

Max f (x) = 3х1+ х2

х1 + х2 £ 5

0.5х1 + х2 ³ 3

х1 - х2 ³ 1

ЗАДАЧА 2.

Используя Поиск решения, решить задачу оптимального использования ресурсов на максимум общей стоимости. Ресурсы сырья, норма его расхода на единицу продукции и цена продукции заданы в соответствующей таблице.

В каждой задаче требуется:

1. Определить план выпуска продукции из условия максимиза­ции его стоимости.

2. Определите ценность каждого ресурса (двойственные оценки) и его приори­тет при решении задачи увеличения запаса ресурсов.

3. Определите суммарную стоимостную оценку ресурсов, ис­пользуемых при производстве единицы каждого изделия. Выпуск какой продукции нерентабелен?

4. На сколько уменьшится стоимость выпускаемой продукции при принудительном выпуске единицы нерентабельной про­дукции?

Кроме того, в каждом варианте необходимо выполнить еще два пункта задания.

Вариант 1

Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице.

Тип	Нормы расхода сырья на одно изделие	Запасы
сырья	А	Б	В	Г	сырья
I
II
III
Цена изделия

5. Определить, как изменятся общая стоимость продукции и план ее выпуска при увеличении запасов сырья I и II вида на 4 и 3 единицы соответственно и уменьшении на 3 единицы сырья III вида.

6. Определить целесообразность включения в план изделия «Д» ценой 10 ед., на изготовление, которого расходуется по две единицы каждого вида сырья ед.

Вариант 2

Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице.

Тип	Нормы расхода сырья на одно изделие	Запасы
сырья	А	Б	В	Г	сырья
I
II
III
Цена изделия

5. Определить, как изменятся общая стоимость продукции и план выпуска при увеличении запасов сырья II и III вида на 120 и 160 ед. соответственно и одновременном уменьшении на 60 ед. запасов сырья I вида;

6. Определить целесообразность включения в план изделия «Д» ценой 12 ед., на изготовление которого расходуется по две единицы каждого вида сырья.

Вариант 3

Для изготовления трех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице.

Тип	Нормы расхода сырья на одно изделие	Запасы
Сырья	А	Б	В	сырья
I
II
III
Цена

5. Определить, как изменится общая прибыль продукции и план выпуска при увеличении запасов сырья I и III вида на 4 ед. каждого;

6. Определить целесообразность включения в план изделия «Г», на изготовление которого расходуется соответственно 1, 3 и 2 ед. каждого вида сырья ценой 13 ед. и изделия «Д» на изготовление которого расходуется по две единицы каждого вида сырья ценой 12 ед.

Вариант 4

Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице.

Тип	Нормы расхода сырья на одно изделие	Запасы
Сырья	А	Б	В	Г	сырья
I
II
III
Цена изделия

5. Определить, как изменится общая стоимость продукции и план выпуска при увеличении запасов сырья I и II вида на 8 и 10 ед. соответственно и одновременном уменьшении на 5 ед. запасов сырья III вида;

6. Определить целесообразность включения в план изделия «Д» на изготовление которого расходуется по две единицы каждого вида сырья и ожидается прибыль 10 ед.

Вариант 5

На основании информации приведенной в таблице была решена задача оптимального использования ресурсов на максимум общей стоимости.

Ресурсы	Нормы затрат ресурсов на единицу продукции	Запасы
	I вид	II вид	III вид
Труд
Сырье
Оборудование
Цена

5. Определить, как изменится общая стоимость продукции и план выпуска при увеличении запасов сырья на 18 единиц;.

6. Определить целесообразность включения в план изделия четвертого вида на изготовление которого расходуется по две единицы каждого вида ресурсов ценой 70 ед.

Вариант 6

На предприятии выпускается три вида изделий, используется при этом три вида сырья:

Сырье	Нормы затрат ресурсов на единицу продукции	Запасы
	А	Б	В	сырья
I
II
III
Цена

5. Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если запас сырья I вида увеличить на 45 кг., а II - уменьшить на 9кг.?

6. Целесообразно ли выпускать изделие Г ценой 11 единиц, если нормы затрат сырья 9, 4 и 6 кг.?

Вариант 7

Для изготовления трех видов продукции используют четыре вида ресурсов. Запасы ресурсов, нормы расхода и цена каждого продукта приведены в таблице.

Ресурсы	Нормы затрат ресурсов на единицу продукции	Запасы
	I вид	II вид	III вид
Труд
Сырье 1
Сырье 2
Оборудование
Цена

5. Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если запас сырья I вида увеличить на 24?

6. Целесообразно ли выпускать изделие четвертого вида ценой 11 единиц, если нормы затрат ресурсов 8, 4, 20 и 6 единиц.?

Вариант 8

Предприятие выпускает 4 вида продукции и использует 3 типа основного оборудования: токарное, фрезерное, шлифовальное. Затраты на изготовление единицы продукции приведены в таблице; там же указан общий фонд рабочего времени, а также цена изделия каждого вида.

Тип	Нормы расхода сырья на одно изделие	Общий фонд
оборудования	А	Б	В	Г	раб. времени
Токарное
Фрезерное
Шлифовальное
Цена изделия

5. Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если фонд времени шлифовального оборудования увеличить на 24 часа?

6. Целесообразно ли выпускать изделие «Д» ценой 11 единиц, если нормы затрат оборудования 8, 2 и 2 ед.?

Вариант 9

На предприятии выпускается три вида изделий, используется при этом три вида сырья:

Сырье	Нормы затрат ресурсов на единицу продукции	Запасы
	А	Б	В	сырья
I				430 кг
II				460 кг
III				420 кг
Цена

5. Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если запас сырья I вида увеличить на 80 кг., а II - уменьшить на 10кг.?

6. Целесообразно ли выпускать изделие Г ценой 7 единиц, если нормы затрат сырья 2, 4 и 3 кг.?

Вариант 10

Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице.

Тип	Нормы расхода сырья на одно изделие	Запасы
Сырья	А	Б	В	Г	сырья
I			0,5
II
III
Цена изделия	7,5

5. Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если запас сырья I вида увеличить на 100 кг, а II - уменьшить на 150кг.?

6. Целесообразно ли выпускать изделие «Д» ценой 10 единиц, если нормы затрат сырья 2, 4 и 3 кг?

Список литературы, имеющейся в библиотеке ВЗФЭИ.

1. Федосеев В.В., Гармаш А.Н., Дайитбегов Д.М., Орлова И.В., Половников В.А. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В.Федосеева. – М.: ЮНИТИ, 1999. – 391 с.

2. Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в среде ЕХСЕL / Практикум: Учебное пособие для вузов. - М.:ЗАО Финстатинформ, 2000.-136 с.

[1] Примечание: Адреса ячеек во все диалоговые окна удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, чьи адреса следует ввести.

[2] Относительные и абсолютные ссылки. В зависимости от выполняемых задач в Excel можно использовать относительные ссылки, определяющие положение ячейки относительно положения ячейки формулы, или абсолютные ссылки, которые всегда указывают на конкретные ячейки. Если перед буквой или номером стоит знак доллара, например, $A$2, то ссылка на столбец или строку является абсолютной. Относительные ссылки автоматически корректируются при их копировании, а абсолютные ссылки — нет.

[3] Адреса ячеек во все диалоговые окна удобно вводить не с клавиатуры, а протаскивая мыщь по ячейкам, чьи адреса следует ввести.

Дата добавления: 2015-03-31