Матрица R1

Результат корреляционного анализа

Анализ матрицы коэффициентов парной корреляции начнем с анализа первого столбца матрицы, в котором расположены коэффициенты корреляции, отражающие тесноту связи зависимой переменной Прибыль (убыток) с включенными в анализ факторами.

Анализ показывает, что зависимая переменная, то есть прибыль, имеет тесную связь с долгосрочными обязательствами (ryX2 = 0,867), с краткосрочной дебиторской задолженностью (ryX4 = 0,654) и с запасами готовой продукции (ryX6 = 0,840).

Затем перейдем к анализу остальных столбцов матрицы с целью выявления коллинеарности. Факторы X2 и X6 достаточно тесно связаны между собой (r = 0,7), что свидетельствует о наличии коллинеарности. Из этих двух переменных оставим X2 – долгосрочные обязательства, так как rX2y = 0,867 > rX6y = 0,840.

Таким образом, на основе анализа только корреляционной матрицы остаются два фактора – Долгосрочные обязательства и Краткосрочную дебиторскую задолженность (n = 50, k =2).

Одним из условий классической регрессионной модели является предположение о независимости объясняющих переменных.

В нашем примере из двух тесно связанных друг с другом факторов Х2 и Х6 (= 0,7) один, Х6, был исключен.

Для выявления мультиколлинеарности факторов выполняем тест Фаррара–Глоубера.

1. Проверка наличия мультиколлинеарности всего массива переменных.

Построим матрицу межфакторных корреляций R1и найдем ее определитель det[R1] = 0,742 с помощью функции

МОПРЕД.

	X2	X4
X2		0,508
X4	0,508

Вычислим наблюдаемое значение статистики Фаррара–Глоубера по следующей формуле:

FG набл = - [n - 1- (2k + 5)]ln(det[R1]) = - [49 – 9/6]*ln(0,742) =

= -47,5 * (-0,298) = 14,155,

где n = 50 – количество наблюдений,

k = 2 – количество факторов.

Фактическое значение этого критерия FGнабл сравниваем с табличным значением χ при k(k – 1) = 1 степенях свободы и уровне значимости α = 0,05. Табличное значение можно найти с помощью функции ХИ2.ОБР.ПХ.

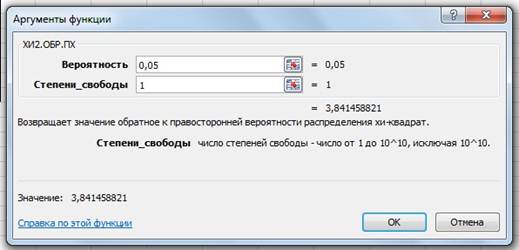
Получение табличного значения χ

Так как FGнабл > FGкрит (14,155 > 3,841), то в массиве объясняющих переменных существует мультиколлинеарность.

2. Проверка наличия мультиколлинеарности каждой переменной с другими переменными

Вычислим обратную матрицу C =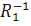

	X2	X4
X2	1,347825	-0,6847
X4	-0,6847	1,347825

Вычислим F-критерии Fj=(Cjj-1) (n-k-1)/k,

где Сjj- диагональные элементы матрицы С:

F2	F4
8,174	8,174

Фактические значения F-критериев сравниваем с табличным значением Fтабл = 3,841 при ν1 = 2 и ν2 = (n – k – 1) = 47 степенях свободы и уровне значимости α = 0,05, где k – количество факторов.

Так как F2 > Fтабл и F4 > Fтабл, то независимые переменные Х2 и

Х4 мультиколлинеарны.

3. Проверка наличия мультиколлинеарности каждой пары переменных

Вычислим частные коэффициенты корреляции по формуле

rij = - 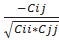, где Сjj – элементы матрицы С.

R2,4 = 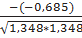= 0,508

Вычислим t-критерии по формуле

tij=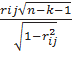

tij= 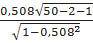= 4,043

Фактические значения t-критериев сравниваются с табличным

значением при степенях свободы (n – k – 1)=47 и уровне значимости α = 0,05: tтабл =2,012. Так как | t2,4 | > tтабл и r2,4= 0,508 => 1, то между независимыми переменными Х2 и Х4 существует мультиколлинеарность.

Далее сделаем тест на выбор «длинной» и «короткой» регрессии.

Алгоритм проверки следующий:

1. Построим по МНК «длинную» регрессию по всем факторам

Х2, …, Хk и найдем для нее сумму квадратов остатков ESSдлин.

2. Построим по МНК «короткую» регрессию по первым (k – q)

факторам Х2, …, Хk–q и найдем для нее сумму квадратов остатков

ESSкор.

3. Вычислим F-статистику:

Fнабл =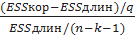

Fнабл=	7,755
Fтабл=	18,513

4. Если Fнабл > Fтабл, то гипотеза отвергается (выбираем «длинную» регрессию), в противном случае – «короткую» регрессию.

В нашем случае Fнабл = 7,755 < Fтабл = 18,513, следовательно, рационально использовать короткую регрессию.

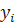= 246094,77 + 0,27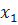

Выбор факторных признаков для построения регрессионной модели методом исключения

Для проведения регрессионного анализа используем инструмент Регрессия (надстройка Анализ данных в Excel).

На первом шаге строится модель регрессии по всем факторам:

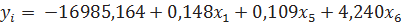
Дата добавления: 2015-03-31