Решение дифференциальных уравнений

Дифференциальные уравнения очень часто встречаются при построении

моделей динамики объектов исследования. Они описывают, как правило, изменения параметров объекта во времени. Результатом решения дифференциальных уравнений являются функции, а не числа, как при решении конечных уравнений, вследствие чего методы решения их более трудоемки.

Дифференциальные уравнения описывают также процессом, тепло-массообмен, изменение концентрации вещества, процессы кристаллизации сахара и многие другие. При использовании численных методов решения дифференциальных уравнений:

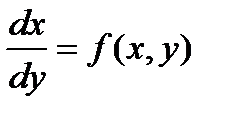или y^’= f (x,y) представляется в табличном виде, т.е. получается
dx совокупность значений Y_i и X_i.

Решение носит шаговый характер, т.е. по одной или нескольким начальным точкам (х, у) за один шаг находят следующую точку и т.д. Разница между двумя соседними значениями аргумента h = x_i+1 - x_i называется шагом.

Наибольшее распространение имеют задачи Коши, в которых заданы начальные условия: при x = x₀, y(x₀) = y₀. Имея их, легко начинать процесс решения, т.е. найти 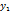при x₁ , y₂ - при х₂ и т.д.

Основная идея получения простейших вычислительных алгоритмов в одношаговых методах сводится к разложению исходного решения у(х) в ряд Тейлора.

Количество оставленных членов ряда определяет порядок и, следовательно, точность метода. По полученному разложению, зная значения у в точке разложения у_i и производную f(x_i, y_i), находят значения у через шаг h:
y_i+1 = y_i + ∆y_i.

Если в разложении удерживается большее число членов, то необходимо рассчитывать f(x_i, y_i) в несколько точках (таким способом избегают необходимости прямого вычисления высших производных, присутствующих в разложении в ряд Тейлора).

Расчётные алгоритмы многошаговых методов базируются на построении интерполяционных или аппроксимирующих функций, от которых берётся интеграл.

Численными методами решаются не только отдельные уравнения, но и системы уравнений (чаще всего первого порядка), причем большинство методов решения одного уравнения легко распространяются на решения систем.

К классу одношаговых методов относятся методы Эйлера,
Рунге – Кутта и Эйлера-Коши.

Функциональное уравнение у¢ = f(x,у), связывающее между собой независимую переменную, искомую функцию у(х) и ее производную у (х), называется дифференциальным уравнением 1-го порядка.

Решением (частным) решением уравнения на интервале (а, b) называется любая функция у = (х), которая, будучи подставлена в это уравнение вместе со своей производной ¢ (x) обращает его в тождество относительно xÎ (а,b). Уравнение Ф. (х,y) = 0, определяющее это решение как неявную функцию, называется интегралом дифференциального уравнения. На плоскости с фиксированной декартовой прямоугольной системой координат уравнение Ф (х,y) =0 определяет некоторую кривую, которая называется интегральной кривой дифференциального уравнения.

Если в дифференциальном уравнении у¢ = f(x,у) функция f(x,у) непрерывна в некоторой области D, плоскости Оху и имеет в этой области ограниченную частную производную (x,y), то для любой точки (x₀,y₀) Î D, в некотором интервале х₀ — h £ х £ х₀ + h, существует и притом единственное решение у (х) этого уравнения, удовлетворяющее начальному условию

у (х_о) - у_о.

Это утверждение известно как теорема Коши о существовании и единственности решения дифференциального уравнения с заданным начальным условием.

Для задач подобного типа, выделенных в целый класс задач Коши, помимо аналитических методов решения разработаны методы численного решения.

Метод Эйлера

Значения искомой функции у= у (х) на отрезке [x₀,X] находят по формуле:

y_k+1 = y_k + h×f(x_k, y_k), (1)

где у_к = у (х_к), х_к+1 = x_k + h, (х_п = Х), k = 0,1,2,...n -1 и h =

По заданной предельной абсолютной погрешности e начальный шаг вычислений h устанавливают с помощью неравенства h² < .

Метод Эйлера - Коши

Для вычисления значений функции у= у (х) применяют формулу:

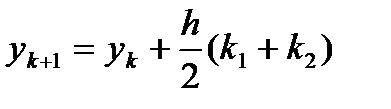(2)

где , , ,

По заданной предельной погрешности начальный шаг вычислений h устанавливается с помощью неравенства h³ < .

Метод Руге - Кутта

Значения искомой функции у= у (х) на отрезке [x₀, X] последовательно находят по формулам:

По заданной предельной абсолютной погрешности начальный шаг вычислений h устанавливают с помощью неравенства h⁴ < .

Правило Рунге - Ромберга

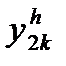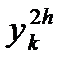Пусть и - значения искомой функции, полученные одним из указанных методов при шагах вычисления h и 2h соответственно, а - заданная абсолютная предельная погрешность. Тогда считается, что достигнута заданная точность вычислений, если выполняется неравенство:

(4)

при всех k и при s = 2,3,4 соответственно для методов Эйлера, Эйлера - Коши, Рунге - Кутта. Решением задачи является функция .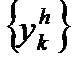

Применяя указанное правило, последовательно вычисляют значения искомой функции с шагом 2h и с шагом h и сравнивают полученные результаты по формуле (4). Вычисления заканчивают, когда неравенство (4) выполняется при всех k.

Оптимизация тех. процесса

Метод дихотомии(метод пол.деления)

Метод дихотомии (деление интервала поиска [a, b] пополам) реализуется следующим алгоритмом:

1. Проверяем условие |b-a|<2E, где E – заданная погрешность вычисления x_n. Если это условие выполняется, идём к п.6; если не выполняется, идём к п.2.

2. Делим интервал поиска [a, b] пополам и вычисляем две абсциссы, симметрично расположенные относительно точки

x=(a + b)/2

x₁=(a + b - E)/2 и x₂=(a + b + E)/2

3. Для этих значений x вычисляем F(x₁)>F(x₂).

4. Проверяем условие F(x₁)>F(x₂). Если оно выполняется, полагаем b=x₂ и идём к п.1. Если не выполняется, идём к п.5.

5. Полагаем a=x₁ и идём к п.1.

6. Выводим на печать x_n=(a+b)/2 и вычисляем F(x_n).

Метод золотого сечения

Золотое сечение проводит деление отрезка АВ на две неравные части так, чтобы было справедливо соотношение (рис. 7).

А С В

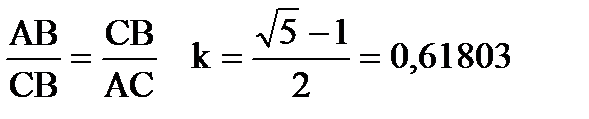Рис. 7

Метод золотого сечения позволяет сужать отрезок [a, b] каждый раз вычисляя лишь одно значение F(x), а не два, как в методе дихотомии.

Данный метод реализуется следующим алгоритмом:

1. Находим коэффициент дробления k=(√5-1)/2 отрезка [a, b].

2. Находим абсциссу х₁=a + (1-k)*(b-a) и вычисляем F(x₁).

3. Находим абсциссу х₂=a + k*(b-a) и вычисляем F(х₂).

4. Проверяем выполнение условия |x₂-x₁|<E, где E – заданная погрешность вычисления x_n. Если это условие выполняется, вычисляем x_n = (x₁+ x₂)/2 и F(x_n), после чего останавливаем счёт с выдачей значений x_m и F(x_n). Если данное условие не выполняется, идём к п.5.

5. Проверяем условие F(x₁) < F(x₂). Если оно выполняется, полагаем, а = х₁, х₁ = х₂ и F(x₁) = F(x₂), после чего идём к п.3. и п.4.

Если F(x₁) ≥ F(x₂), полагаем b = x₂, x₂ = x₁, f(x₁) = f(x₂), после чего выполняем п.2 и п.4

Использование ППП Eureka и Excel при решении задач оптимизации

Использование ППП Eureka для поиска экстремумов функций одной переменной.

Для поиска максимумов функций одной переменной необходимо в окне Edit набрать

$|__|max(F)

y(x)=

F=y(x)

В окне Solution будет выдано решение

F=

x=

Перед решением задачи весьма полезно оценить вид функции, экстремум которой необходимо найти и уточнить интервал x, в котором этот экстремум находится. Для этого достаточно воспользоваться командой Plot в позиции Graf основного меню. Из вида графика сделать вывод о правильности решения.

Использование ППП Excel для поиска экстремумов функций одной переменной.

Для поиска максимумов функций одной переменной необходимо:

Вызвать Подбор параметра, с помощью команды в меню Сервис. Окно Подбор параметра состоит из трех полей:

- Установить целевую ячейку, в котором ставится ссылка на ячейку с формулой (Y);

- Равной – выбираем максимальному значению;

- Изменяя ячейки, в которой ставится ссылка на ячейку с изменяемым параметром (первая граница, а интервала (а,в)).

Метод Фибоначчи

В методе Фибоначчи точка деления интервала исследования определяется с каждым новым расчётом (в методе дихотомии необходимо на каждом шаге выполнять два расчёта). В интервал исследования попадет предыдущий расчёт и для продолжения поиска достаточно произвести расчёт симметрично имеющемуся.

Допустим, задано число расчётов (шагов) N. Необходимо их произвести так, чтобы интервал, в котором лежит оптимум, был минимальным. Числа Фибоначчи, используемые в этом методе, определяются следующим образом:

F_N=F_N-1+F_N-2

F₀=F₁=1

Алгоритм метода Фибоначчи состоит из следующих этапов:

1) Изменяют масштаб исходного интервала, в котором лежит оптимум. В качестве единицы измерения принимают 1=X₀/F_N, или если задана длина l, в котором лежит оптимум, находят его на исходном интервале длиной X₀. Для этого, разделив X₀ на 1, находят ближайшее большее число Фибоначчи F_N,
а по нему определяют N – число необходимых расчётов для определения интервала.

2) Расставляют первые две точки и на интервале исследования X₀ на расстоянии F_N-2 от конца b.

3) Вычисляют значение целевой функции в этих точках для сужения интервала исследования. Пусть 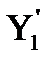> , тогда интервал [ , F_N] исключается из рассмотрения.

4) На новом интервале исследования снова расставляют две точк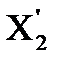и и , но в одной из них уже известно значение целевой функции = .

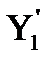5) Переходят к этапу 3 и т.д., пока не достигают искомого интервала, в котором находится значение переменной, максимизирующее её целевую функцию.

Дата добавления: 2015-03-29