Общий вид транспортной задачи

Транспортная задача

Транспортная работа - это особый класс задач линейного программирования. Задача заключается в отыскании такого плана перевозок продукции с m складов в пункт назначения n который, потребовал бы минимальных затрат. Если потребитель j получает единицу продукции (по прямой дороге) со склада i, то возникают издержки Сij. Предполагается, что транспортные расходы пропорциональны перевозимому количеству продукции, т.е. перевозка k единиц продукции вызывает расходы k С i j.

Математическая модель

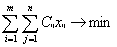
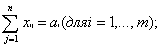
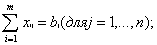
где xij количество продукции, поставляемое со склада i потребителю j, а С i j издержки (стоимость перевозок со склада i потребителю j).

Если условие 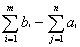равны, то транспортная задача называется сбалансированной т. е. закрытой.

Если данное условие не выполняется, то задача называется несбалансированной или открытой и вводится либо фиктивный пункт производства, либо фиктивный пункт назначения.

Далее,

где ai есть количество продукции, находящееся на складе i, и bj - потребность потребителя j.

Замечание(для открытых задач)

1. Если сумма запасов в пунктах отправления превышает сумму поданных заявок 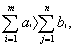то количество продукции, равное остается на складах. В этом случае мы введем "фиктивного" потребителя n +1 с потребностью и положим транспортные расходы pi,n +1 равными 0 для всех i.

2. Если сумма поданных заявок превышает наличные запасы 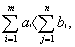то потребность не может быть покрыта. Эту задачу можно свести к обычной транспортной задаче с правильным балансом, если ввести фиктивный пункт отправления m + 1 с запасом 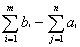и стоимость перевозок из фиктивного пункта отправления во все пункты назначения принять равным нулю.

Дата добавления: 2015-03-29