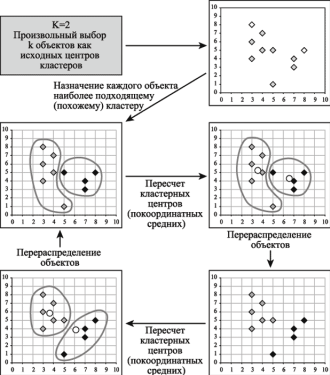
Алгоритм k-средних (k-means)

Итеративные методы.

Иерархические агломеративные методы (Agglomerative Nesting, AGNES)

Иерархические методы.

Методы кластерного анализа.

Сети с обратными связями

Сети без обратных связей

- Сети с обратным распространением ошибки. Сети этой группы характеризуются фиксированной структурой, итерационным обучением, корректировкой весов по ошибкам.

- Другие сети (когнитрон, неокогнитрон, другие сложные модели).

- Сети Хопфилда (задачи ассоциативной памяти).

- Сети Кохонена (задачи кластерного анализа).

Методы кластерного анализа можно разделить на две группы:

 иерархические (иерархические методы кластерного анализа используются при небольших объемах наборов данных, результат – древовидная диаграмма);

 неиерархические.

Суть иерархической кластеризации состоит в последовательном объединении меньших кластеров в большие или разделении больших кластеров на меньшие.

Эта группа методов характеризуется последовательным объединением исходных элементов и соответствующим уменьшением числа кластеров.

Иерархические дивизимные (делимые) методы (DIvisive ANAlysis, DIANA). Эти методы являются логической противоположностью агломеративным методам. В начале работы алгоритма все объекты принадлежат одному кластеру, который на последующих шагах делится на меньшие кластеры, в результате образуетсяпоследовательность расщепляющих групп.

Используются при большом количестве наблюдений и представляют собой итеративные методы дробления исходной совокупности. В процессе деления новые кластеры формируются до тех пор, пока не будет выполнено правило остановки.

В отличие от иерархических методов, которые не требуют предварительных предположений относительно числа кластеров, при использовании этих методов необходимо иметь гипотезу о наиболее вероятном количестве кластеров.

Существует два подхода. Первый заключается в определении границ кластеров как наиболее плотных участков в многомерном пространстве исходных данных, т.е. определение кластера там, где имеется большое "сгущение точек". Второй подход заключается в минимизации меры различия объектов.

Итеративные методы показывают более высокую устойчивость по отношению к шумам и выбросам, некорректному выбору метрики, включению незначимых переменных в набор, участвующий в кластеризации.

Основной тип задач, которые решает алгоритм k-средних - наличие предположений (гипотез) относительно числа кластеров, при этом они должны быть различны настолько, насколько это возможно. Общая идея алгоритма: заданное фиксированное число k кластеров наблюдения сопоставляются кластерам так, что средние в кластере (для всех переменных) максимально возможно отличаются друг от друга.

Дата добавления: 2015-03-31