Производная высших порядков

Производная обратной функции.

Производная суммы, произведения и частного.

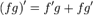
3. Производная сложной функции.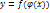

Функция 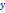является сложной функцией аргумента .

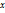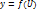
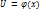
Если выполнены 2 условия

1) 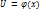имеет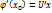

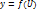
2) 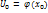имеет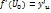

Тогда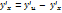

Функция g(x) является обратно для функции f(x) если выполняется 2 условия

1) Если для любого g(y) 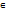D(g) выполнено равенство f(g(y)) = y

2) x 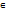D(f) и выполнено равенство y(f(x)) = x.

Свойства взаимообратных функций.

А) Если f обратная функция для g, тогда справедливо обратное, g обратная функция для f.

Б) Взаимообратные функции строго монотонны и непрерывны.

Пример: а) y = ln(x) D(y) = (0; + inf) E(y) = (-inf; + inf).

x = e^y D(y) = (-inf; + inf) E(y) = (0; + inf).

Понятие производной произвольного порядка задаётся рекуррентно. Полагаем

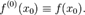
Если функция 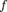дифференцируема в 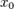, то производная первого порядка определяется соотношением

Пусть теперь производная 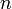-го порядка 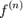определена в некоторой окрестности точки 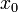и дифференцируема. Тогда

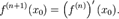
Если функция 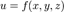имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от 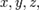может иметь в некоторой точке 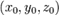частные производные по той же или по любой другой переменной. Для исходной функции 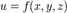эти производные будут частными производными второго порядка (или вторыми частными производными).

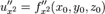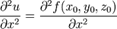
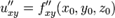или

или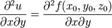

Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,

Дата добавления: 2015-03-31