П.4. Прямое многократное измерение

П.3. Прямое однократное измерение

Однократные измерения физических величин наиболее являются наи­более часто встречающимися и наиболее распространенными. Нужно, правда отметить, что этот термин практике технических измерений, с одной сто­роны, и в практике метрологических и научно-исследовательских работ, с другой, понимаются различно. Здесь мы рассматриваем понятие «однократ­ное измерение» прежде всего в его метрологическом смысле.

Все составляющие погрешности однократного прямого измерения оце­нивается до его выполнения. Основой для оценки погрешности служит ана­лиз всей имеющейся информации о проведении данных измерений, источни­ком которой могут служить техническая документация на средства измере­ний, опыт проведения подобных измерений, данные научно-исследователь­ских работ и пр.

По результатам анализа устанавливают величину неисключенного ос­татка систематической погрешности q и среднеквадратическое отклонение случайной погрешности s и устанавливают их соотношение.

· При q < 0,5s пренебрегают неислюченным остатком и величину погрешно­сти измерений принимают обычно равной D=2s.

· При q > 8s пренебрегают случайной составляющей погрешности и пола­гают D=q.

· В промежуточных случаях (0,5s<q<8s) погрешность находят по формуле D=0,8(q+2s). Коэффициент 0,8 учитывает малую вероятность того, что систематическая и случайная погрешности одновременно имеют свои максимальные значения.

· В случаях, когда главным источником погрешности является инструмен­тальная, а всеми остальными можно пренебречь, анализ составляющих погрешности не производится. Результат измерений представляется в виде A±D, где А – показание средства измерений, D- погрешность, опре­деляемая его классом точности.

Случайная составляющая погрешности может быть уменьшена при проведении многократных измерений физической величины в одинаковых условиях. Интуитивно понятно (и может быть доказано математически), что при бесконечно большом количестве измерений, выполняемых в строго оди­наковых условиях, можно полностью исключить случайную составляющую погрешности и найти истинное значение физической величины

Ø Истинное значение физической величины равно ее точному сред­нему значению по всей бесконечно большой совокупности идентичных измерений.

Однако реально мы всегда имеем дело с ограниченным количеством измерений. Поэтому вместо точного среднего значения можно получить только некоторую его оценку, которая будет определяться законом распре­деления вероятности величины случайной погрешности и количеством изме­рений.

Эта оценка является случайной величиной (в отличие от собственно сред­него значения, которое является величиной неслучайной). Значение этой оценки зависит от числа измерений, закона распределения вероятности по­грешности отдельного измерения и определяется в соответствии с законами и критериями теории вероятности и математической статистики.

Раньше уже отмечалось, что истинное значение измеряемой физиче­ской величины не может быть получено из опыта и на практике используется ее действительное значения. Указанная вероятностная оценка среднего зна­чения, определенная таким образом, и есть действительное значение физиче­ской величины, полученное в многократных измерениях.

Ø За действительное значение физической величины принима­ется ее среднеарифметическое значение - наиболее достовер­ное значение, которое можно приписать измеряемой величине на основании многократных измерений.

Среднеарифметическое значение физической величины А, полученное в результате многократных измерений, равно:

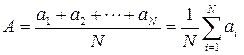(1.8)

где a_i - результат i -го отдельного измерения, N – число измерений.

Величина, которая характеризует отклонение среднеарифметического значения измеренной физической величины от его среднего значения, назы­вается дисперсией среднеарифметического (среднеквадратичное значение отклонение), которая равна:

(1.9)

где: - среднее значение измеряемой величины, равное истинному значе­нию, s- среднеквадратичная погрешность однократного измерения.

Из (1.9) следует, что дисперсия среднеарифметического в N меньше дисперсии отдельного измерения.

Таким образом:

· Если за действительное значение принять среднеарифметическое зна­чение измеренной физической величины, то среднеквадратиче­ское отклонение, которое характеризует случайную составляющую погрешности результата многократного измерения, в раз меньше среднеквадратичного отклонения результата однократного измерения.

Точно так же, как невозможно определить среднее значение величины, нельзя определить и среднеквадратическое значение отклонения отдельного измерения s. При конечном числе измерений N, возможно лишь найти его оценку, которая равна:

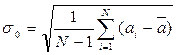(1.10)

Для многократного измерения оценка среднеквадратического отклонения среднеарифметического равна:

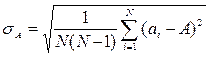(1.10а)

Ø При увеличении количества измерений N ® ¥ среднеарифмети­ческое значение А стремится к среднему зна­чению, а среднеквадратическая погрешность становится пре­небрежимо малой s_А ® 0.

Рассмотренные среднеарифметическое значение и среднеквадратичное отклонение есть случайные величины, которые характеризуют измеряемую величину в единственной точке и являются «точечными» оценками погреш­ности измерений. Наряду с этим типом оценки существует и.«интервальная» оценка погрешности

Интервальная оценка погрешности состоит в указании доверительного интервала, в котором измеряемая величина находится с известной вероятно­стью. Согласно этой оценке определяется вероятность появления погрешно­сти d, величина которой не выходит за некоторые принятые границы (интер­вал). За середину этого интервала принимается среднеарифметическое зна­чение величины, а сам интервал называют доверительным интервалом,

При нормальном законе распределения с помощью значения интеграла ошибок Ф(t) можно вычислить вероятность того, что величины случайной погрешности лежит в некотором заданном интервале значений. В частности:

· P (-3s < d < 3s) = 2Ф(3) = 0,9972

случайная составляющая погрешности измерения с вероят­ностью 0,9972 не выходит за пределы интервала ±3s

· P (-2,67s < d <2,6s) = 2Ф(2,6) = 0,99,

случайная составляющая погрешности измерения с вероят­ностью 0,99 лежит в пределах ±2,6s

· P (-2s < d < 2s) = 2Ф(2) = 0,95

случайная составляющая погрешности измерения с вероят­ностью 0,95 лежит в пределах интервала ±2s.

· Р(- (-s < d < s) = 2Ф (1) = 0,68

Вероятность того, что величина погрешности не превышает своего среднеквадратического значения составляет 0,68

Т.к. вероятность появления ошибки в пределах -¥<d<+¥ равна 1, то ве­роятность превышения величины погрешности среднеквадратического зна­чения составляет 1-0,68=0,32, а вероятность появления погрешности по абсо­лютной величине большей 3s, равна 1-0,9972 =0,0028. Т.е. в этом случае из 370 измерений только в одном величина ошибки будет лежать вне интервала ±3s.

Ø Вероятной погрешностью называют такую погрешность, от­носительно которой при повторных измерениях 50% слу­чайных погрешностей будет по абсолютной величине больше вероятной погрешности, а другие 50% - меньше ее.

Т.е. вероятная погрешность равна доверительному интервалу, при ко­тором доверительная вероятность равна 0,5. При нормальном законе распре­деления вероятная погрешность результата измерений, т.е. погреш­ность определения среднеарифметического значения, будет равна

Все вышесказанное относится к случаям, когда число отдельных изме­рений достаточно велико, N ³ 30. Тогда с высокой степенью точности можно считать, что среднеарифметическое значение измеряемой величины равно среднему, которое и принимается за действительное значение. При этом среднеквадратическое отклонение отдельного измерения s ₀ равно средне­квадратическому отклонению многократного измерения s _А и соответствую­щему параметру закона нормального распределения s.

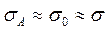
На практике количество измерений достаточно ограничено и для опре­деления доверительного интервала при нормальном распределении резуль­тата отдельного измерения вместо интеграла ошибок используют закон рас­пределение ошибок Стьюдента и соответствующий интеграл, значения кото­рого тоже табулированы в виде коэффициентов Стьюдента t_N, Эти коэффи­циенты зависят от задаваемой доверительной вероятности Р и количества измерений N (таблица 1.4.). Для определения доверительного интервала среднеквадратическая погрешность s_А умножается на коэффициент Стью­дента, взятый из соответствующей таблицы, и границы доверительного ин­тервала записываются в виде:

(1.11)

Понятие о доверительном интервале используется для выявления гру­бых ошибок. Если результат отдельного измерения выходит за пределы до­верительных границ, то это нарушение статистической закономерности с принятой доверительной вероятностью можно рассматривать как проявление грубой погрешности. Такой результат должен быть отброшен и все расчеты проведены заново.

При N> 30 принято отбрасывать результаты отдельных измерений, от­личающихся от среднеарифметического более, чем на 3s₀ =3s, т.к. вероят­ность их появления менеzе 0,003. Отсюда следует правило 3s:

Ø При нормальном законе распределения за максимальную вели­чину случайной составляющей погрешности величину принимают ее значении, равное трем значениям средне­квадратичной погрешности

Погрешности более, чем второе превосходящие среднеквад­ратичное значение считаются грубыми и исключаются из дальнейшего рассмотрения.

Поясним на следующем примере. Пусть с помощью стрелочного вольтметра измерялось напряжение в электрической сети газа. Измерения выполнялись 8 раз, их результаты приведены в таблице 1.5.

№ пп.
Измеренное значение, В
Погрешность отдельного измерения, В	+2	+4	-10	-8	+15	+3	-1	-5

Среднеарифметическое значение измеренного напряжения, которое мы принимаем за его действительное значение, равно 224 В. Тогда можно вы­числить погрешности отдельных измерений также приведены в таблице, и рассчитать среднеквадратическое отклонение:

Определим интервал, в котором измеряемого напряжения находится с доверительной вероятностью 99%. Для этого по таблице коэффициентов рас­пределения Стъюдента для доверительной вероятности Р=0,99 и N =8 нахо­дим t_n = 3,5. Отсюда согласно формуле (1.11) находим величину напряже­ния: U =224 В ± 3 ´ 3,5 В= (224±10,5) В = (224±11) В. При определении чис­ленного значения мы учли, что данные измерений известны с точностью 1 В, поэтому все вычисляемые значения также округляются до 1 В.

Полученная оценка показывает, что погрешность одного из измерений (№ 5) не укладывается в установленный доверительный интервал, т.е. содер­жит грубую погрешность. Это значение должно быть исключено, а проце­дура определения погрешности проведена заново, но при количестве измере­ний N =7. В результате мы получим, что с вероятностью 0,99 действительное значение напряжения лежит в пределах (221±8) В.

Дата добавления: 2015-03-31