Существенное замечание относительно прямых измерений

· На практике в чистом виде этот способ измерений встречаются только в достаточно простых ситуациях, например измерение напряжения в элек­трической сети аттестованным вольтметром. В большинстве случаев ко­нечный результат измерений получается только после неоднократного преобразования измерительного сигнала (в измерительном преобразова­теле, вторичных преобразователях, линиях связи, каждый со своим коэф­фициентом передачи), введения калибровочных коэффициентов, физиче­ских констант, поправочных коэффициентов, в том числе и на изменение параметров окружающей среды, и т.п. Т.е. в результате выполнения опре­деленной вычислительной процедуры, которая, по сути, соответствует косвенным измерениям.

· Погрешность прямых измерений должна определяться с уче­том погрешности всех возможных ее источников, которые рассчитываются так же, как и погрешности косвенных изме­рений.

Более полным и строгим подходом к определению величины случай­ной погрешности косвенных измерений является метод, основанный на пред­ставлении искомой физической величины в виде ряда Тэйлора.

Пусть величина Z является функцией двух величин X и Y, значения ко­торых получены в прямых измерениях. Будем полагать, что величины X и Y есть действительные значения соответствующих физических величин, тогда можно записать:

(1.16)

(1.16а)

Будем полагать величину погрешностей малой по сравнению с дейст­вительными значениями величин и представим результирующую погреш­ность ∆ в виде суммы неисключенного остатка систематической погрешно­сти (НСП) θ и случайной составляющей δ

Разложим функцию F(X,Y) в ряд Тэйлора. Тогда для погрешности косвен­ного измерения нетрудно получим следующее выражение:

(1.17)

Если теперь усреднить левую и правую части этого уравнения и учесть, что средняя величина случайной погрешности стремится к нулю, то для система­тической погрешности косвенного измерения получим:

(1.18)

Из уравнений () и () вытекает несколько следствий.

1. Первое из них заключается в том, что систематическая погрешность косвенных измерений определяется не только величиной НСП прямых изме­рений величин X и Y, но и случайной погрешностью их измерения. Необхо­димость введения поправок в результаты косвенного измерения согласно () может возникнуть даже если при прямых измерениях НСП равна нулю, θ_X = θ_Y =0, но величина случайной погрешности d_X и (или) d_Y достаточно велика.

2. Если ограничиться в разложении Тэйлора только членами первого порядка, то из сравнения уравнений (1.17) и (1.18) можно получить выра­жение для случайной составляющей погрешности, по форме аналогичное (1.16):

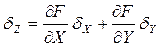
Отсюда нетрудно получить выражение для дисперсии (квадрата сред­неквадратического значения) случайной погрешности косвенного измерения:

(1.19)

где есть корреляционный момент, который служит мерой линейной статистической связи случайных величин X и Y, при этом знак R_XY указывает на характер связи.

Эта статистическая связь определяется характером объекта и методи­кой проведения измерений и может носить самый разнообразный характер. Отличие корреляционного момента от нуля, R_XY ≠ 0, означает, что по каким-то причинам случайные величины X и Y обнаруживают тенденцию к син­хронному изменению под воздействием каких-либо внешних факторов, на­пример, температуры внешней среды.

Их изменение может быть однонаправленным, R_XY >0 – положительная корреляция, которая приведет к увеличению погрешности косвенного изме­рения, или разнонаправленным, R_XY <0 - отрицательная корреляция, следст­вием которой будет уменьшение результирующей погрешности. При R_XY =0 корреляция отсутствует и величины X и Y будут независимы (некоррелиро­ваны).

Из краткого рассмотрения погрешностей многократного измерения вы­текает очень существенное соображение, которое заключается в следующем:

· На практике при оценке погрешности измерений точность ис­пользуемых средств измерения очень часто не играет опреде­ляющей роли. Главное внимание должно уделяться анализу метода измерений и его конкретной реализацией, взаимодей­ствию методов и средств измерения с объектом измерений и окружающей средой.

Дата добавления: 2015-03-31