П.5. Косвенные измерения

Результат косвенных измерений получается в итоге выполнения некой вычислительной процедуры над данными прямых измерений и погрешность прямых измерений, естественно, оказывает непосредственное влияние на окончательную погрешность косвенных измерений.

Пусть определяемая в процессе косвенных измерений неизвестная ве­личина Z есть функция нескольких (i) величин X _i, значения которых можно получить из опытных данных и значения которых, по сути, являются дейст­вительными значениями соответствующих физических величин.

(1.11)

причем эта функция F непрерывна и дифференцируема (заметим, что в про­тивном случае косвенные измерения не имеют физического смысла). Пусть также систематическая и случайная составляющая погрешности величин X_i равны соответственно q_I и s:

DX_i=q_i+s_i

и пусть все составляющие этих погрешностей нам известны и их можно считать малыми.

Возможны два подхода к оценке величины результирующей погреш­ности измерений величины Z.

При первом подходе, который наиболее часто используется в обычной практике, оценивается результирующие абсолютная и относительная по­грешности косвенного измерения, но нет возможности разделить их на сис­тематическую и случайную составляющие, оценить их статистические харак­теристики.

Продифференцируем уравнение (1.11) и получим:

(1.12)

Если от дифференциалов перейти к конечным приращениям, (кото­рыми по физической сущности являются погрешности), то получим выраже­ния для абсолютной и относительной погрешности косвенного измерения, выраженные через соответствующие погрешности прямых измерений:

(1.13)

(1.13а)

где:

Рассмотрим два типичных случая.

а). Пусть . Тогда относительная погрешность d_z косвенного измерения величины Z, выраженная через случайные погрешности величин X и Y, согласно формуле () будет равна:

. (1.14)

Отсюда видно, что, при значениях показателей степени n, m > 1 вклад погрешности прямого измерения в результирующую относительную погреш­ность косвенного измерения будет усиливаться пропорционально показателю степени.

б). Пусть . Величина относительной погрешности косвен­ного измерения, полученная из уравнения (..), будет равна:

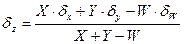(1.15)

Следовательно, если измеренные значения величин X, Y, W таковы, что удовлетворяют условию X+Y»W, то результирующая погрешность кос­венного измерения величины Z, как следует из (1.15), может оказаться весьма велика. Причем даже случае, когда погрешности измерения величин X, Y и W достаточно малы, d_X, d_Y, d_W ® 0.

Из этих примеров ясно видно, что при выборе метода косвенного изме­рения физической величины надо очень внимательно подходить к анализу физических законов и соответствующих вычислительных процедур, кото­рыми определяется связь этой величины с измеряемыми параметрами.

Дата добавления: 2015-03-31