Измерительные преобразователи прямого и компенсационного преобразования

В любом средстве измерений, в том числе и в электроизмерительных приборах, измерительный сигнал проходит цепь последовательных физических и (или) математических преобразований, в результате которых из сигнала из­влекается информация об измеряемой физической величине. В аналоговых средствах измерений все преобразования происходят в электронных или элек­тромеханических элементах электрической измерительной цепи.

· Преобразовательный элемент – элемент измерительной цепи, в котором происходит одно из последовательных преобразований измерительной информации,:

· Измерительный преобразователь – один или несколько преобразовательных элементов, объединенных функционально и конструктивно.

В линейной измерительной цепи (схеме прямого преобразования) на входе измерительного преобразователя мы имеем электрический сигнал в виде тока I или напряжения U, на его выходе сигнал Y, который функционально связан с измеряемой физической величиной (рис. 2.48). Каждый элемент измерительной цепи может быть характеризован коэффициентом передачи (или чувствительно­стью) равным отношению сигнала на выходе элемента к сигналу на его входе, S_i=Х_вых/Х_вх, и величиной внутреннего комплексного сопротивления (импедан­сом)этого элемента, Z. Изменение сигнала на входе (D I или D U) вызывает из­менение выходного сигнала D Y, а общий коэффициент передачи линейной из­мерительной цепи S _пр будет равен произведению коэффициентов передачи всех ее звеньев:

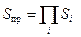
В зависимости от соотношения между внутренним сопротивлением (импе­дансом) источника сигнала и входным импедансом измери­тельной цепи (прибора), которая является нагрузкой для этого источника, в измерительных преобразователях различают коэффициент передачи по току и коэффициент передачи по напряжению.

Ø Если импеданс измерительной цепи (прибора) много больше внутреннего сопротивления источника сигнала, Z_пр >> Z_ис, то мы будем иметь коэффициент преобразования по напряжению (чувствительность по напряжению),

S_U = DU/DY

Ø Если импеданс измерительного прибора много меньше внутреннего сопротивления источника,, Z _пр << Z_ип, то измерительный преобразователь характеризуется коэффициентом передачи по току (чувствительность по току),

S_I = DI/DY

Соответственно изменение сигнала на выходе преобразователя будет свя­зано с изменением сигнала на его входе соотношением для коэффи­циента передачи по напряжению или 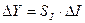для коэффициента пере­дави по току.

В схемах прямого преобразования изменение чувствительности элементов линейной измерительной цепи приводит к появлению мультипликативной по­грешности. При этом абсолютная погрешность измерения входной величины любого элемента измерительной цепи будет пропорциональна самой входной величине DХ=X·(DS/S), а относительная погрешность всей измерительной цепи будет равна сумме погрешностей, вносимых каждым из ее элементов.

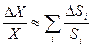
В измерительных преобразователях «дрейф нуля», наложение помех на по­лезный сигнал и другие причины вызывают смещение а _nфункции преобразова­ния каждого из элементов и, соответственно другой тип погрешности – адди­тивную погрешность. Абсолютная погрешность, вносимая этим видом погреш­ности для каждого из элементов не зависит от величины сигнала и равна Dх = а _n, а для всей измерительной цепи относительная аддитивная погрешность будет приблизительно равна:

Ø В средствах измерений, построенных по схеме прямого преобразования, происходит сложное суммирование погрешностей, которые вносят все отдельные звенья измерительной цепи. Очевидно, что в этом случае создать средства измерений высокой точности крайне затруднительно.

Для уменьшения результирующей погрешности измерений применяют схемы компенсационного преобразования, в которой измерительная цепь

состоит из двух цепей – цепи прямого преобразования и цепи отрицательной обратной связи по выходному сигналу (рис 2.49). На входе прямой цепи происходит сравнение измеряемой величины Х и выходной величины цепи обратной связи, равной выходной величине цепи прямого преобразования Y, умноженной на коэффициент передачи цепи обратной связи k. Выходной сигнал схемы будет определяться величиной коэффициента передачи в прямой и обратной цепях:

Следовательно, при большой величине коэффициента обратной связи k·S_пр >>1 выходной сигнал практически не будет зависеть от коэффициента передачи цепи прямого преобразования.

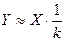
Ø Результирующая погрешность в компенсационной измерительной цепи определяется единственным параметром - нестабильностью коэффициента обратной связи DY/Y = Dk/k.

Компенсационные измерительные цепи являются частным случаем метода сравнения и реализуются в измерительных преобразователях сравнения - мостовых, дифференциальных и потенциометрических.

Дата добавления: 2015-03-31