
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 10. Статистические методы изучения взаимосвязей 1 страница
|
|
|
|
Подписано в печать с оригинал-макета 17.04.08.
Учебное пособие
Часть II. Железнодорожный транспорт
ЭКОНОМИКА ТРАНСПОРТА
ЕФАНОВ АЛЕКСЕЙ НИКИТОВИЧ
Редактор Г. Н. Кириллова
Компьютерная верстка Н. А. Старковой
Формат 60 х 84 1/16. Бумага для множ. апп. Печать офсетная.
Усл. печ. л. 8,75. Уч.-изд. л. 8,75. Тираж 150 экз.
Заказ
Петербургский государственный университет путей сообщения.
190031, СПб., Московский пр., 9.
[*] На рубеже XXI века трубопроводный транспорт оттеснил железнодорожный на второе место.
1 Единая тарифно-статистическая номенклатура грузов.
* Год построения тарифов МТТ.
* В настоящее время – Федеральная служба по тарифам.
[3] Это позволит высвободить в 2030 г. финансовые ресурсы в экономике страны в размере 2,0 трлн. руб. по сравнению с 2006 годом по максимальному варианту и 1,0 трлн. руб. – по минимальному варианту.
[4] По оценке Института системного анализа РАН Российской Федерации индекс-мультипликатор дли инвестиций в железнодорожный транспорт равен 3.
Цель занятия: Освоить методику применения статистических методов для изучения взаимосвязей социально-экономических явлений.
Методические указания. Задача 1. Охарактеризуйте зависимость урожайности зерновых от качества почвы (табл. 259), рассчитав параметры нижеследующих функций: а) линейной, б) степенной, в) экспоненты, г) показательной, д) равносторонней гиперболы, е) обратной и т.д. Определите показатели тесноты связи для каждой модели, оценив каждую из них по показателю детерминации, F-критерию Фишера, ошибку апроксимации и выбрать наилучшую из них. Для расчетов используйте программы Statgraphics, статистические функции ЛИНЕЙН, ЛГРФПРИБЛ в MS Excel, инструмент анализа данных Регрессия и т.д.
Решение: для определения формы связи между урожайностью зерновых культур и качеством почвы построим график (рис. 29). На оси абсцисс нанесем значение независимой переменной (качество почвы), на оси ординат - зависимой (урожайность).
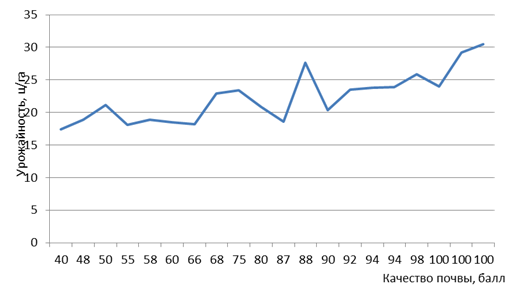
Рис. 29. Зависимость урожайности от качества почвы
а) рассмотрим линейную функцию, выраженную уравнением прямой линии:
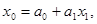 (63)
(63)
где 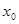 - урожайность зерновых, ц/га;
- урожайность зерновых, ц/га;
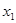 - качество почвы, бал.;
- качество почвы, бал.;
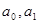 - параметры уравнения связи, которые следует определить на основе решения системы нормальных уравнений с двумя неизвестными:
- параметры уравнения связи, которые следует определить на основе решения системы нормальных уравнений с двумя неизвестными:
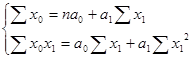 (64)
(64)
Для удобства расчетов заполним таблицу 259.
Таблица 259 - Данные для уравнения связи и коэффициента корреляции
| № хозяйства | Урожайность зерновых, ц/га 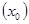
| Качество почвы, балл 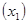
| Расчетные данные | Ожидаемое значение урожайности в зависимости от качества почвы 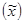
| 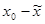
| 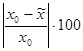
| ||
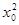
| 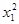
| 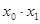
| ||||||
| 17,3 | 299,29 | 17,7944 | -0,2737 | 1,582081 | ||||
| 17,9 | 320,41 | 751,8 | 18,0862 | -0,2191 | 1,224022 | |||
| 21,2 | 449,44 | 18,5239 | 2,5355 | 11,95991 | ||||
| 20,5 | 420,25 | 18,9616 | 1,2901 | 6,293171 | ||||
| 21,2 | 449,44 | 1017,6 | 18,9616 | 1,4447 | 6,814623 | |||
| 18,6 | 345,96 | 1134,6 | 20,8583 | -1,7007 | 9,143548 | |||
| 19,5 | 380,25 | 1267,5 | 21,4419 | -1,3461 | 6,903077 | |||
| 19,8 | 392,04 | 1306,8 | 21,5878 | -1,5915 | 8,037879 | |||
| 22,755 | 2,0631 | 8,59625 | ||||||
| 21,2 | 449,44 | 22,9009 | -1,2823 | 6,048585 | ||||
| 19,5 | 380,25 | 1540,5 | 23,4845 | -3,5277 | 18,09077 | |||
| 24,214 | 4,4269 | 15,81036 | ||||||
| 22,5 | 506,25 | 1912,5 | 24,3599 | -1,6185 | 7,193333 | |||
| 24,5058 | -0,6639 | 2,76625 | ||||||
| 24,5 | 600,25 | 2131,5 | 24,6517 | -0,7093 | 2,895102 | |||
| 22,5 | 506,25 | 2137,5 | 25,8189 | -3,2547 | 14,46533 | |||
| 24,3 | 590,49 | 26,5484 | -2,0001 | 8,230864 | ||||
| 30,5 | 930,25 | 26,5484 | 3,6545 | 11,98197 | ||||
| 28,5 | 812,25 | 26,5484 | 1,1091 | 3,891579 | ||||
| 29,6 | 876,16 | 26,5484 | 1,6637 | 5,620608 | ||||
| Итого | 455,1 | 10644,67 | 34902,3 | 455,1 | 2,1316E-14 | 157,5493 |
Данные таблицы 259 занесем в систему уравнения.
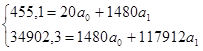
Разделив оба уравнения на коэффициент при 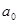 , т.е. первое на 20, второе - на 1543, получим:
, т.е. первое на 20, второе - на 1543, получим:
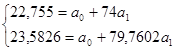
Вычтем из большего уравнения меньшее, в данном случае из второго первое:
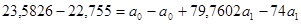 .
.
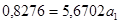
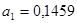
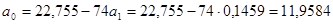
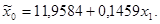
Решим задачу методом определителей: определитель системы 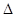 равен:
равен:
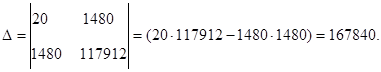
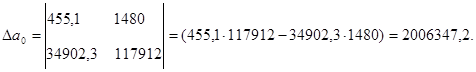
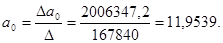
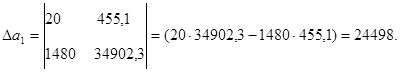
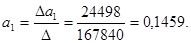
Уравнение регрессии составит: 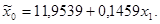
Используя статистическую функцию ЛИНЕЙН в MS Excel (Windows 7) получим следующее решение (рис. 30).
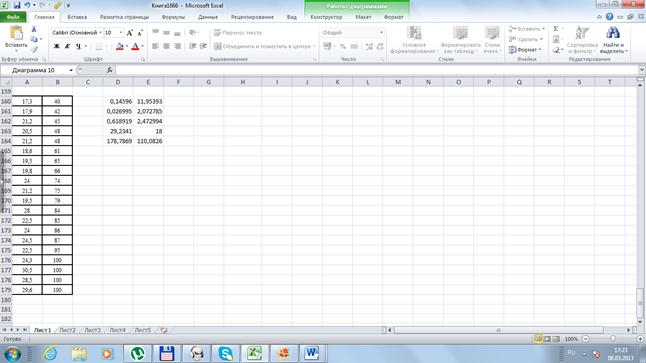
Рис. 30. Регрессионная статистика функции ЛИНЕЙН
Мы получили следующую функцию 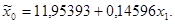 Коэффициент детерминации составил 0,62.
Коэффициент детерминации составил 0,62.
Коэффициент регрессии (параметр 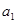 ), равный 0,1459, показывает, что с увеличением балла почвы на единицу урожайность в данных конкретных условиях возрастает на 0,1459 ц/га.
), равный 0,1459, показывает, что с увеличением балла почвы на единицу урожайность в данных конкретных условиях возрастает на 0,1459 ц/га.
Определим тесноту связи между изучаемыми признаками, для чего рассчитаем коэффициент корреляции по формулам:
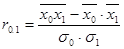 . (65)
. (65)
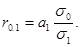 (66)
(66)
Для определения коэффициента корреляции надо определить средние значения 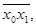
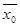 ,
, 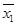 , а также средние квадратические отклонения по результативному и факторному признакам. Все исходные и расчетные данные имеются в таблице 259.
, а также средние квадратические отклонения по результативному и факторному признакам. Все исходные и расчетные данные имеются в таблице 259.
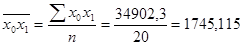 ,
,
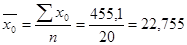 ,
, 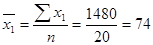 ,
,
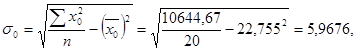
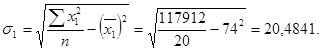
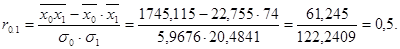
Коэффициент парной линейной корреляции можно рассчитать и по другой формуле, если известен коэффициент регрессии:
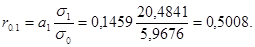
Рассчитанный коэффициент корреляции показал существенную зависимость урожайности зерновых от качества почв. Коэффициент детерминации 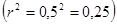 показывает, что на 25 % урожайность в данных условиях зависит от качества почвы, а на 75 % - от других факторов, которые не рассматривались в задаче.
показывает, что на 25 % урожайность в данных условиях зависит от качества почвы, а на 75 % - от других факторов, которые не рассматривались в задаче.
Рассчитаем F-критерий Фишера по формуле:
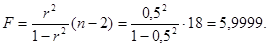
Если возьмем коэффициент детерминации по данным рис. 30, то получим следующий F-критерий Фишера:
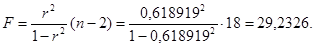
Этот расчет совпадает с рис. 30.
Табличное значение F-критерий Фишера составило 4,41. Так как фактическое значение F превышает табличное, уравнение регрессии статистически значимо.
Определим среднюю ошибку апроксимации по формуле:
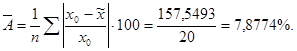
Этот показатель не выше 8 - 10 %, т.е. среднее отклонение расчетных 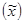 и фактических
и фактических 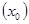 данных не столь велико.
данных не столь велико.
Решим эту задачи с помощью программы Statgraphics:
1) Откроем таблицу данных и введем значения;
2) В главном меню выберем Ralate/ Simple Regression;
3) Заполним поля у и х, нажмем на OK три раза (рис. 31…33) и получаем результат (рис. 34).
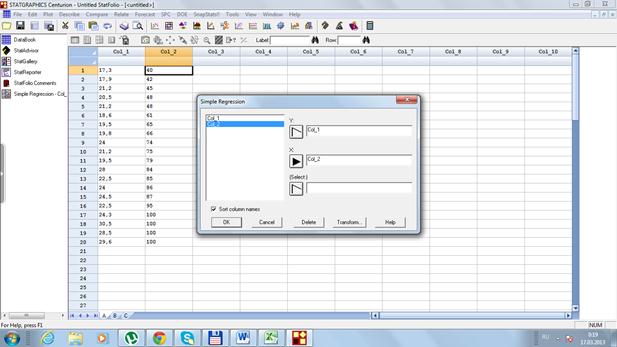
Рис. 31. Диалоговое окно Simple Regression
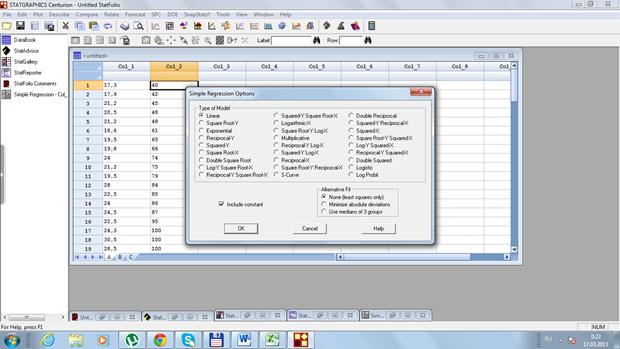
Рис. 32. Диалоговое окно Simple Regression Options
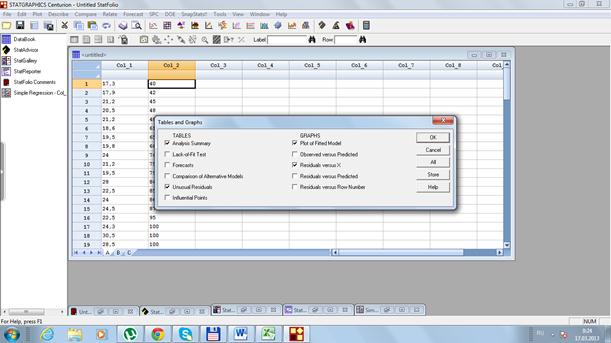
Рис. 33. Диалоговое окно Tables and Graphs
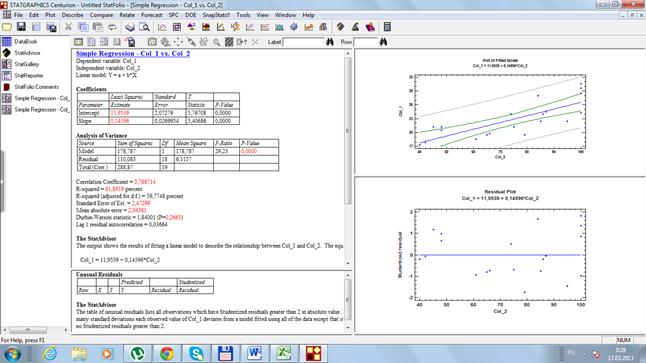
Рис. 34. Результаты расчетов
Определим эмпирическое корреляционное отношение по формуле:
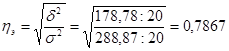 или 78,68.
или 78,68.
Определим теоретическое корреляционное отношение по формуле:
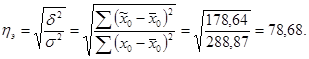
Таким образом, мы получили те же значения и уравнение регрессии составило: 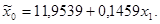 Из рисунка 34 видно, что случайные ошибки параметров
Из рисунка 34 видно, что случайные ошибки параметров 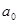 и
и 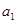 равны
равны 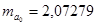 и
и 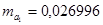 . Эти значения указывают на величину, сформировавшуюся под воздействием случайных факторов. На их основе рассчитываются значения t-критерия Стьюдента:
. Эти значения указывают на величину, сформировавшуюся под воздействием случайных факторов. На их основе рассчитываются значения t-критерия Стьюдента: 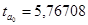 и
и 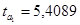 . На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости
. На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости 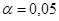 , т.е. с вероятностью 0,95 составит 2,1098,
, т.е. с вероятностью 0,95 составит 2,1098, 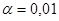 , т.е. с вероятностью 0,99 – 2,8982. Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров (
, т.е. с вероятностью 0,99 – 2,8982. Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров (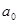 и
и 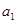 ), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так
), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так 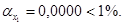 То есть вероятность случайно получить такое значение t-критерия Стьюдента составляет 0,0000, что не превышает допустимый уровень значимости 5 %.
То есть вероятность случайно получить такое значение t-критерия Стьюдента составляет 0,0000, что не превышает допустимый уровень значимости 5 %.
Чуть ниже на рис. 34 представлен расчет F-критерий Фишера, и он составляет 29,23. Согласно дисперсионному анализу вероятность получить случайно такое значение F-критерий Фишера составляет 0,0000, что не превышает допустимый уровень значимости 5%.
Отсюда же берем нескорректированный коэффициент детерминации 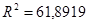 , который оценивает долю вариации результата в зависимости от факторов в общей вариации. Этот показатель показывает на достаточно высокую связь результата и от факторного признака. Скорректированный коэффициент детерминации
, который оценивает долю вариации результата в зависимости от факторов в общей вариации. Этот показатель показывает на достаточно высокую связь результата и от факторного признака. Скорректированный коэффициент детерминации 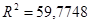 оценивает тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов.
оценивает тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов.
Помощью инструмента анализа данных Регрессия получим следующие данные (рис. 35).
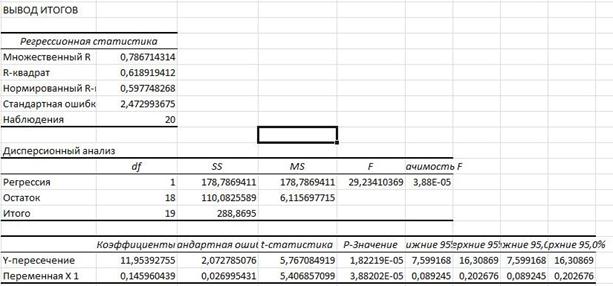
Рис. 35. Регрессионная статистика
Как видим из рис. 35 уравнение регрессии полностью совпадает.
б) рассмотрим степенную функцию:
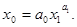 (67)
(67)
Линеаризуем модель логарифмированием:
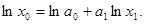
Пусть 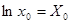 ,
, 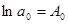 ,
, 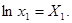
Тогда получим линейное уравнение: 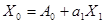 .
.
Для удобства расчетов заполним таблицу 260.
Таблица 260 - Данные для уравнения связи и индекса корреляции
| № хозяйства | 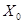
| 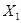
| 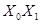
| 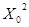
| 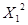
| 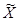
| 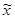
| 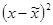
| 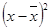
|
| 2,850707 | 3,688879 | 10,51591 | 8,126528 | 13,60783 | 2,879097 | 17,7982 | 0,248206 | 29,75703 | |
| 2,884801 | 3,73767 | 10,78243 | 8,322075 | 13,97017 | 2,898926 | 18,15464 | 0,064843 | 23,57103 | |
| 3,054001 | 3,806662 | 11,62555 | 9,326923 | 14,49068 | 2,926966 | 18,67089 | 6,39639 | 2,418025 | |
| 3,020425 | 3,871201 | 11,69267 | 9,122966 | 14,9862 | 2,953195 | 19,16709 | 1,776646 | 5,085025 | |
| 3,054001 | 3,871201 | 11,82265 | 9,326923 | 14,9862 | 2,953195 | 19,16709 | 4,132719 | 2,418025 | |
| 2,923162 | 4,110874 | 12,01675 | 8,544874 | 16,89928 | 3,0506 | 21,12802 | 6,390899 | 17,26403 | |
| 2,970414 | 4,174387 | 12,39966 | 8,823362 | 17,42551 | 3,076413 | 21,68049 | 4,754532 | 10,59503 | |
| 2,985682 | 4,189655 | 12,50898 | 8,914297 | 17,55321 | 3,082618 | 21,81543 | 4,061964 | 8,732025 | |
| 3,178054 | 4,304065 | 13,67855 | 10,10003 | 18,52498 | 3,129115 | 22,85375 | 1,313896 | 1,550025 | |
| 3,054001 | 4,317488 | 13,18561 | 9,326923 | 18,6407 | 3,13457 | 22,97876 | 3,16399 | 2,418025 | |
| 2,970414 | 4,369448 | 12,97907 | 8,823362 | 19,09207 | 3,155687 | 23,46916 | 15,75425 | 10,59503 | |
| 3,332205 | 4,430817 | 14,76439 | 11,10359 | 19,63214 | 3,180628 | 24,06187 | 15,5089 | 27,51003 | |
| 3,113515 | 4,442651 | 13,83226 | 9,693978 | 19,73715 | 3,185438 | 24,17787 | 2,81526 | 0,065025 | |
| 3,178054 | 4,454347 | 14,15616 | 10,10003 | 19,84121 | 3,190191 | 24,29307 | 0,085892 | 1,550025 | |
| 3,198673 | 4,465908 | 14,28498 | 10,23151 | 19,94434 | 3,19489 | 24,40748 | 0,00856 | 3,045025 | |
| 3,113515 | 4,553877 | 14,17857 | 9,693978 | 20,73779 | 3,230641 | 25,29587 | 7,816884 | 0,065025 | |
| 3,190476 | 4,60517 | 14,69269 | 10,17914 | 21,20759 | 3,251487 | 25,82872 | 2,336998 | 2,387025 | |
| 3,417727 | 4,60517 | 15,73921 | 11,68086 | 21,20759 | 3,251487 | 25,82872 | 21,82082 | 59,98503 | |
| 3,349904 | 4,60517 | 15,42688 | 11,22186 | 21,20759 | 3,251487 | 25,82872 | 7,135714 | 33,00503 | |
| 3,387774 | 4,60517 | 15,60128 | 11,47702 | 21,20759 | 3,251487 | 25,82872 | 14,22252 | 46,85403 | |
| Итого | 62,22751 | 85,20981 | 265,8842 | 194,1402 | 364,8998 | 62,22812 | 452,4346 | 119,8099 | 288,8695 |
| В среднем | 3,111375 | 4,260491 | 13,29421 | 9,70701 | 18,24499 | 2,879097 | 17,7982 | 29,75703 |
Получим систему нормальных уравнений:
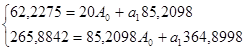
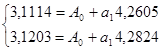
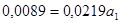
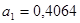
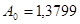
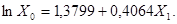
Коэффициент эластичности 0,4064 показывает, что с ростом качества почвы на 1 балл, урожайность зерновых возрастает на 0,41 ц/га.
Если решить эту систему через статистическую функцию ЛИНЕЙН в MS Excel получим следующее уравнение
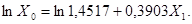
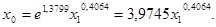
Решим эту задачу с помощью программы Statgraphics (рис. 36).
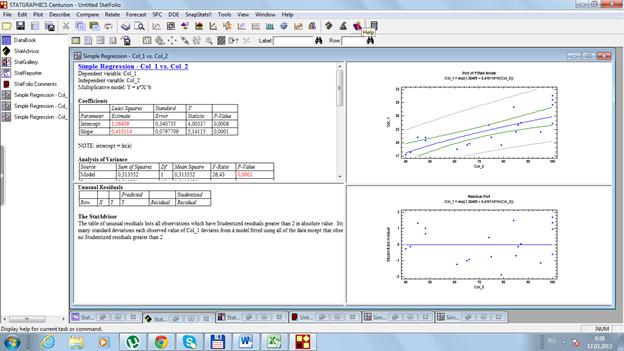
Рис. 36. Результаты расчетов
Получаем уравнение регрессии 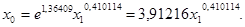 Из рисунка 36 видно, что случайные ошибки параметров
Из рисунка 36 видно, что случайные ошибки параметров 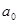 и
и 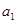 равны
равны 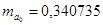 и
и 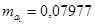 . Эти значения указывают на величину, сформировавшуюся под воздействием случайных факторов. На их основе рассчитываются значения t-критерия Стьюдента:
. Эти значения указывают на величину, сформировавшуюся под воздействием случайных факторов. На их основе рассчитываются значения t-критерия Стьюдента: 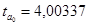 и
и 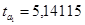 . На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости
. На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости 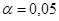 , т.е. с вероятностью 0,95 составит 2,1098,
, т.е. с вероятностью 0,95 составит 2,1098, 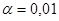 , т.е. с вероятностью 0,99 – 2,8982. Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров (
, т.е. с вероятностью 0,99 – 2,8982. Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров (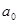 и
и 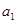 ), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так
), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так 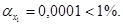 То есть вероятность случайно получить такое значение t-критерия Стьюдента составляет 0,0000, что не превышает допустимый уровень значимости 5 %.
То есть вероятность случайно получить такое значение t-критерия Стьюдента составляет 0,0000, что не превышает допустимый уровень значимости 5 %.
Тесноту связи определим, рассчитав индекс корреляции:
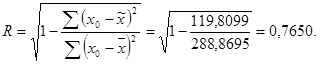
Коэффициент детерминации составил 0,5852, таким образом, на 58,52% вариации 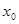 объясняется вариацией
объясняется вариацией 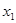 , на долю прочих факторов приходится 23,5 %.
, на долю прочих факторов приходится 23,5 %.
Рассчитаем F-критерий Фишера по формуле:
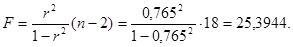
Табличное значение F-критерий Фишера составило 4,41. Так как фактическое значение F превышает табличное, уравнение регрессии 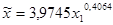 статистически значимо.
статистически значимо.
Чуть ниже (рис. 36) представлен расчет F-критерий Фишера, и он составляет 26,43. Согласно дисперсионному анализу вероятность получить случайно такое значение F-критерий Фишера составляет 0,0001, что не превышает допустимый уровень значимости 5%.
Определим среднюю ошибку апроксимации по формуле:
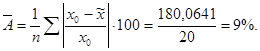
Этот показатель не выше 8 - 10 %, т.е. среднее отклонение расчетных 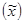 и фактических
и фактических 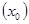 данных не столь велико.
данных не столь велико.
в) рассмотрим функцию экспоненты:
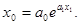 (68)
(68)
Для оценки параметров приведем уравнение к линейному виду:
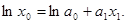
Воспользуемся методом наименьших квадратов и получим систему уравнений:
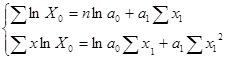
Для удобства расчетов заполним таблицу 261.
Таблица 261 - Данные для уравнения связи и индекса корреляции
| № хозяйства | 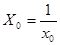
| 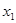
| 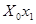
| 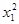
| 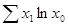
| 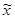
| 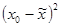
| 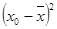
| 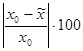
|
| 0,0578 | 2,3121 | 114,0283 | 18,0970 | 0,6352 | 29,757 | 0,0461 | |||
| 0,0559 | 2,3464 | 121,1616 | 18,3279 | 0,1831 | 23,571 | 0,0239 | |||
| 0,0472 | 2,1226 | 137,4301 | 18,67984 | 6,3512 | 2,4180 | 0,1189 | |||
| 0,0488 | 2,3415 | 144,9804 | 19,03853 | 2,1360 | 5,0850 | 0,0713 | |||
| 0,0472 | 2,2642 | 146,5921 | 19,03853 | 4,6720 | 2,4180 | 0,1020 | |||
| 0,0538 | 3,2796 | 178,3129 | 20,67416 | 4,302147 | 17,2640 | 0,1115 | |||
| 0,0513 | 3,3333 | 193,0769 | 21,20516 | 2,90762 | 10,5950 | 0,0874 | |||
| 0,0505 | 3,3333 | 197,055 | 21,34003 | 2,3717 | 8,7320 | 0,0778 | |||
| 0,0417 | 3,0833 | 235,176 | 22,45032 | 2,4015 | 1,5500 | 0,0646 | |||
| 0,0472 | 3,5378 | 229,0501 | 22,5931 | 1,9407 | 2,4180 | 0,0657 | |||
| 0,0513 | 4,0513 | 234,6627 | 23,1734 | 13,4938 | 10,5950 | 0,1884 | |||
| 0,0357 | 279,9052 | 23,9198 | 16,6484 | 27,5100 | 0,1457 | ||||
| 0,0444 | 3,7778 | 264,6488 | 24,0719 | 2,4708 | 0,0650 | 0,0699 | |||
| 0,0417 | 3,5833 | 273,3126 | 24,2250 | 0,0506 | 1,5500 | 0,0094 | |||
| 0,0408 | 3,5510 | 278,2846 | 24,3791 | 0,0146 | 3,0450 | 0,0049 | |||
| 0,0444 | 4,2222 | 295,784 | 25,6475 | 9,9065 | 0,0650 | 0,1399 | |||
| 0,0413 | 4,1152 | 319,0476 | 26,4735 | 4,7242 | 2,3870 | 0,0894 | |||
| 0,0328 | 3,2787 | 341,7727 | 26,4735 | 16,2126 | 59,9850 | 0,1320 | |||
| 0,0351 | 3,5088 | 334,9904 | 26,4735 | 4,1067 | 33,0050 | 0,0711 | |||
| 0,0338 | 3,3784 | 338,7774 | 26,4735 | 9,7749 | 46,8540 | 0,1056 | |||
| Итого | 0,9024 | 64,4208 | 4658,049 | 452,7551 | 105,3042 | 288,8695 | 1,7255 |
Получим систему нормальных уравнений:
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 446; Нарушение авторских прав?; Мы поможем в написании вашей работы!