Тема 10. Статистические методы изучения взаимосвязей 3 страница

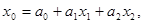(73)

где 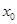- урожайность картофеля, ц/га;

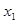- количество внесенных органических удобрений под картофель, т/га;

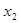- удельный вес посевов высокосортными семенами, %.

Требуется определить параметры уравнения связи коэффициент множественной корреляции.

Решение: Составим систему нормальных уравнений с тремя неизвестными:

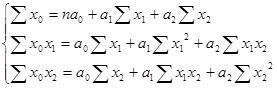(74)

Подставив в эту систему данные из табл. 261, получим:

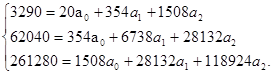
Разделим каждое из уравнений на коэффициенты при первом известном 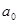: первое уравнение - на 20, второе - на 354, третье - на 1508, получим:

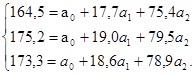
Теперь поочередно вычтем первое уравнение из второго и третьего:

(175,2 - 164,5) = 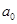- 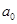+ (19,0 - 17,7) 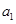+ (79,5 - 75,4) ;

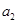(173,3-164,5) = 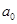- 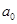+ (18,6 – 17,7) 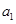+ (78,9 – 75,4) .

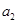Получим:

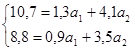
Разделив каждое из двух этих уравнений на коэффициент при 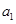, первое уравнение - на 1,3, второе - на 0,9, получим:

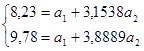
Из второго уравнения вычитаем первое и освобождаемся от параметра 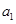: 9,78 -8,23 = (3,8889 - 3,1538)а₂, 1,55 = 0,73 5а₂, отсюда а₂ = 1,55: 0,735 = 2,11. Подставляем значение а₂ в уравнение 8,23 = 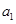+ 3,1538 ∙ 2,11, отсюда 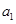= 1,58. Далее надо найти значение параметра а_о, для чего используем уравнение 164,5 = 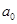+ 17,7 ∙ 1,58 + 75,4 ∙ 2,11. Сделаем соответствующие расчеты: 164,5 = 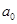+ 27,966 + 159,09; отсюда а₀.= - 22,6. Уравнение множественной линейной зависимости примет вид: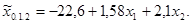

Параметры уравнения множественной регрессии показывают, что с увеличением дозы внесения органических удобрений на 1 т в расчете на 1 га урожайность картофеля возрастает на 1,58 ц, а повышение удельного веса высокосортных семян на 1 % дает прирост урожайности 2,11 ц. Параметр 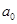экономического смысла не имеет.

Теперь определим тесноту связи. Рассчитаем множественный (совокупный) коэффициент корреляции по формуле

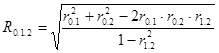(75)

Для его расчета надо найти средние значения 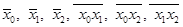, а также средние квадратические отклонения по урожайности, внесению удобрений и удельному весу высокосортных семян:

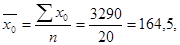
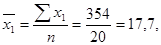
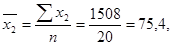
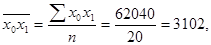
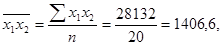
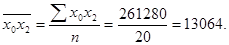
Теперь рассчитаем средние квадратические отклонения:

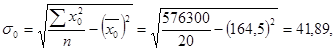
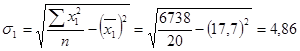
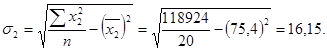
Рассчитаем парные коэффициенты корреляции:

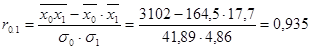
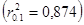
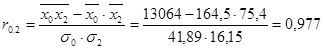
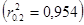
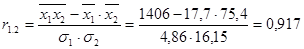
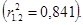
Эти коэффициенты можно рассчитать с помощью MS Excel. В главном меню последовательно выбираем Данные /Анализ данных /Корреляция (рис. 42).

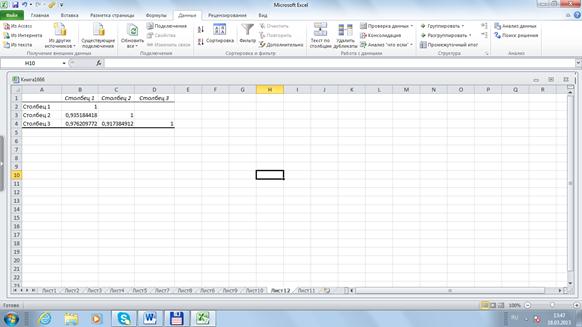
Рис. 42. Расчет коэффициентов корреляции

Так же можно воспользоваться программой Statgraphics, используя в расчетах функцию Multiple Variable Analisis (рис. 43).

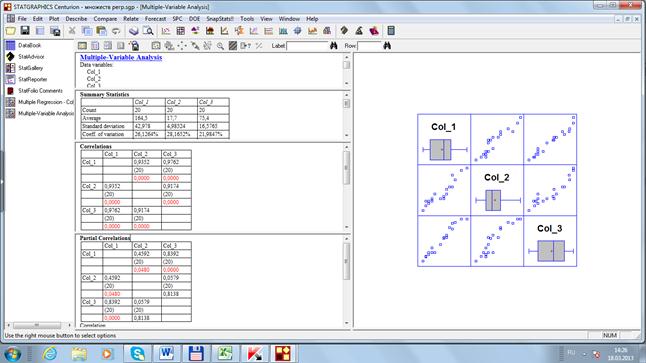
Рис. 43. Расчет коэффициентов корреляции

Подставив значения коэффициента корреляции и детерминации в формулу множественной (совокупной) корреляции получим:

Связь между признаками очень тесная, так как коэффициент множественной корреляции составляет 0,981, а детерминации — 0,962. т.е. 96,2 % колебаний урожайности картофеля в данных условиях зависит от исследуемых факторов и только 3,8 % - от других, не уточненных в анализе.

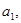
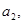
Значимость 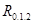оценим t-критерием Стьюдента:

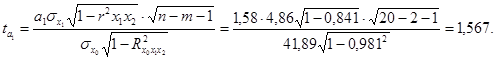
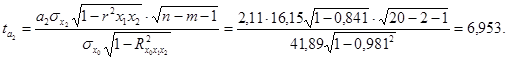
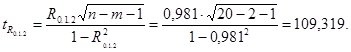
Табличное значение t-критерия Стьюдента при 5 % уровне значимости и 17 степенях свободы (n-m=20-2-1=17) составляет 2,1098. Так как только при условии 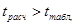оба фактора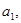 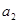, 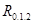считаются значимыми. Однако 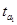меньше положенного. Поэтому величина 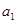является статистически незначимой, ненадежной, т.е. она сформировалась под воздействием случайных факторов. То же касается и величины .

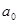Теперь воспользуемся инструментом анализа данных Регрессия (рис. 43).

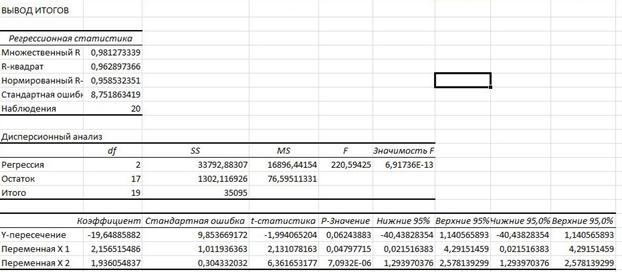
Рис. 43. Результаты расчетов

Уравнение множественной линейной зависимости примет вид: 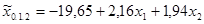. Коэффициент детерминации 0,9629.

Табличное значение F-критерий Фишера составило 3,59, расчетное – 220,59. Так как фактическое значение F превышает табличное, уравнение регрессии статистически значимо.

Решим эту же задачу с помощью программы Statgraphics, используя в расчетах функцию Multiple Regression (рис. 44).

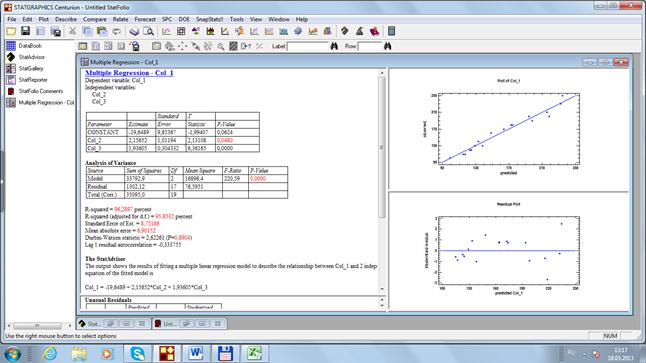
Рис. 44. Результаты расчетов

Уравнение множественной линейной зависимости примет вид: 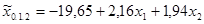. Случайные ошибки параметров 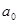, , 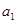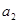равны 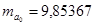, , 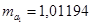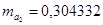. Эти значения указывают на величину, сформировавшуюся под воздействием случайных факторов. На их основе рассчитываются значения t-критерия Стьюдента: 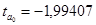, , 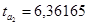. На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости 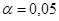, т.е. с вероятностью 0,95 составит 2,1098, 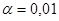, т.е. с вероятностью 0,99 – 2,8982. Статистически значимыми здесь являются 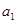, , 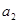а величина 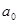сформировалась под воздействием случайных причин.

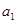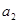Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров ( и ), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так 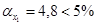и То есть вероятность случайно получить такие значения t-критерия Стьюдента составляет 4,8 % и 0,0000, что не превышает допустимый уровень значимости 5 %.

Чуть ниже на рис. 44 представлен расчет F-критерий Фишера, и он составляет 29,23. Согласно дисперсионному анализу вероятность получить случайно такое значение F-критерий Фишера составляет 0,0000, что не превышает допустимый уровень значимости 5%.

Отсюда же берем нескорректированный коэффициент детерминации 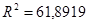, который оценивает долю вариации результата в зависимости от факторов в общей вариации. Этот показатель показывает на достаточно высокую связь результата и от факторного признака. Скорректированный коэффициент детерминации 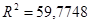оценивает тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов.

Табличное значение F-критерий Фишера составило 3,59, расчетное – 220,59. Так как фактическое значение F превышает табличное, уравнение регрессии 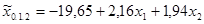статистически значимо.

Задание 3. Определение показателей связи при парной криволинейной зависимости.

Имеются данные по группе коров об их продуктивности возрасте (числе отелов) (табл. 266).

Таблица 266 - Данные для уравнения связи и индекса корреляции (корреляционное отношение)

№ п/п	Исходные данные	Расчетные данные
относительное изменение удоя, %, (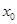)	возраст коров к моменту отела, лет ()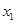
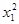
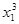
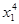
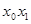
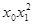
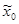
								80,649	198,16	154,45
		2,5	6,25	15,625	39,06		512,5	83,965	122,7	83,032
								86,979	36,929	37,185
		3,5	12,25	42,875	150,06			89,692	1,1598	11,459
								92,103	0,8521	0,9485
								96,021	24,237	8,6676

Продолжение таблицы 266

								98,733	47,929	31,991
								100,24	35,083	51,295
								100,54	35,083	55,683
								99,633	24,237	42,982
								97,521	8,5444	19,75
								94,203	0,8521	1,2681
								89,679	1,1598	11,546
Итого			667,5	6141,5	60898,125		63639,5		536,92	510,26

Анализ исходных данных позволил установить, что зависимость криволинейная и может быть описана уравнением параболы 2-го порядка:

(76)

Требуется определить параметры уравнения связи и индекс корреляции.

Решение: Составим систему уравнений для нахождения параметров , , :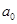

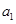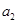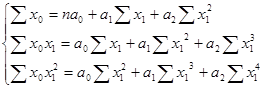
В систему уравнений подставим данные из табл. 266:

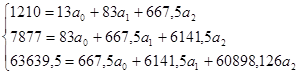
Разделим члены каждого уравнения на коэффициент при а_о

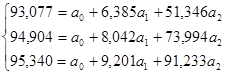
Теперь из второго уравнения вычтем первое, а из третьего - второе:

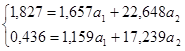
Освободимся от коэффициента при 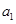, для чего все члены уравнения разделим на коэффициент при :

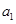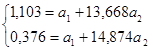
Из первого уравнения вычтем второе и получим 0,727=-1,206 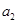, отсюда а₂=-0,603. Подставим значения а₂ в уравнение 1,103= 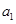+13,668∙(-0,603); отсюда 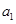= 9,345. В уравнение 93,077 = 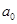+ 6,385 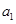+ 51,346a₂ подставим значения найденных параметров 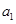и а₂:

93,077 = а₀ + 6,385∙9,345 + 51,346∙(- 0,603);

93,077 = 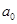+ 59,668 - 30,962;

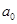= 93,007 - 59,668 + 30,962;

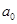= 64,371.

Следовательно, уравнение параболы второго порядка будет иметь следующий вид: 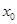= 64,371 + 9,345 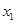- 0,603 .

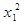Отрицательное значение а₂ показывает, что с увеличением возраста коров до определенного предела (6-го отела) удой возрастает на 9,345 % с каждым новым отелом, а затем после определенного предела (с 6-го отела до 12-го отела) начинает падать в среднем на 0,603 %.

Когда связь между 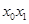нелинейная (в нашем случае - параболическая), для измерения тесноты связи используют корреляционное отношение, которое рассчитывается по формуле:

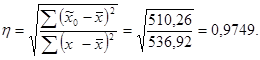
Полученный результат свидетельствует о наличии тесной связи между возрастом коров и их продуктивностью, так как 95,03 % вариации в продуктивности связано с возрастом данной группы коров.

Решим эту же задачу с помощью программы Statgraphics, используя в расчетах функцию Polynomial Regression (рис. 45).

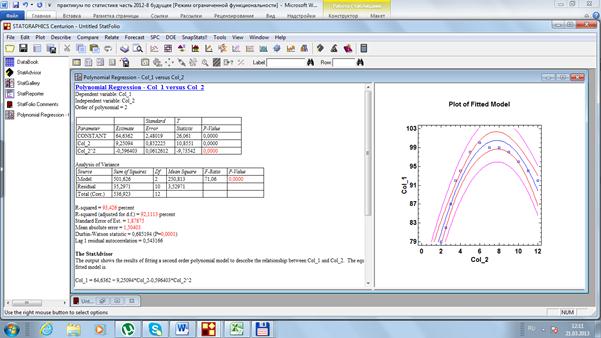
Рис. 45. Результаты расчетов

Уравнение парной криволинейной зависимости примет вид: .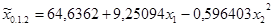

Случайные ошибки параметров 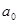, , 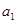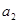равны 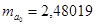, , 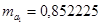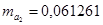. Эти значения указывают на величину, сформировавшуюся под воздействием случайных факторов. На их основе рассчитываются значения t-критерия Стьюдента: 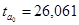, , 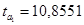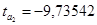. На основе Приложения 2 определим критические значения t-критерия Стьюдента для уровня значимости 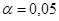, т.е. с вероятностью 0,95 составит 2,2281, 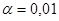, т.е. с вероятностью 0,99 – 3,1693. Статистически значимыми здесь являются , , .

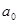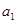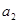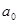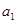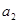Так как фактические значения больше теоретических (критических), то делаем вывод о существенности данных параметров (, и ), которые формируются под воздействием не случайных причин. Об это же свидетельствует показатель вероятности случайных значений параметров регрессии, так 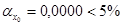, 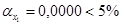и То есть вероятность случайно получить такие значения t-критерия Стьюдента составляет 0,0000 %, что не превышает допустимый уровень значимости 5 %.

Чуть ниже на рис. 45 представлен расчет F-критерий Фишера, и он составляет 71,06. Согласно дисперсионному анализу вероятность получить случайно такое значение F-критерий Фишера составляет 0,0000, что не превышает допустимый уровень значимости 5%.

Отсюда же берем нескорректированный коэффициент детерминации 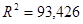, который оценивает долю вариации результата в зависимости от факторов в общей вариации. Этот показатель показывает на достаточно высокую связь результата и от факторного признака. Скорректированный коэффициент детерминации 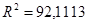оценивает тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов.

Задача 4. Имеются выборочные данные по 12 однородным предприятиям (табл. 267). Определите в программе Statgraphics уравнение регрессии, наиболее полно отражающее исходные данные. Оцените значимость параметров уравнения регрессии с помощью t-критерия Стьюдента и F-критерия Фишера.

Таблица 267 – Исходные данные

№ предприятия	Выпуск готовой продукции на одного рабочего, т	Электровооруженность труда на одного рабочего, кВтч

Построить однофакторную регрессионную модель.

Решение: воспользовавшись программой Statgraphics, получим следующие данные (табл. 268).

Таблица 268 – Уравнения регрессии, коэффициент детерминации и достоверность

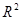
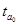
№ п/п	Уравнение регрессии			P		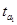P	F	P
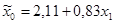
		90,68	4,86	0,007	9,86	0,0000	97,26	0,0000
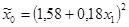
		86,59	14,01	0,0000	8,04	0,0000	64,58	0,0000
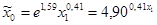
		79,63	7,83	0,0000	6,25	0,0001	39,09	0,0001
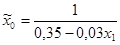
		59,81	7,92	0,0000	-3,86	0,0032	14,88	0,0032
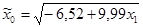
		92,27	-1,38	0,1965	10,93	0,0000	119,4	0,0000
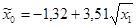
		93,50	-2,11	0,0608	11,99	0,0000	143,80	0,0000
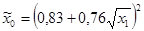
		92,39	5,64	0,0002	11,02	0,0000	121,49	0,0000
		88,32	1,86	0,0932	8,70	0,0000	75,62	0,0000
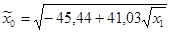
		90,09	-4,93	0,0006	9,53	0,0000	90,90	0,0000
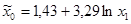
		91,44	3,01	0,0130	10,34	0,0000	106,89	0,0000
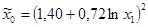
		94,13	16,46	0,0000	12,66	0,0000	160,39	0,0000
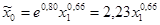
		94,14	10,30	0,0000	12,67	0,0000	160,63	0,0000
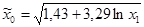
		82,45	-1,43	0,1844	6,86	0,0000	47,00	0,0000
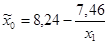
		71,56	14,22	0,0000	-5,02	0,0005	25,17	0,0005
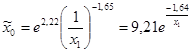
		88,78	30,73	0,0000	-8,90	0,0000	79,15	0,0000
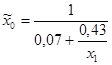
		96,68	6,80	0,0000	17,08	0,0000	291,58	0,0000
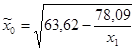
		55,25	7,34	0,0000	-3,51	0,0056	12,35	0,0056
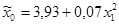
		79,81	9,12	0,0000	6,29	0,0001	39,54	0,0001
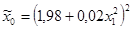
		72,60	18,18	0,0000	5,15	0,0004	26,50	0,0004
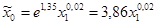
		63,14	11,73	0,0000	4,14	0,0020	17,3	0,0020
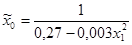
		41,68	7,49	0,0000	-2,67	0,0234	7,15	0,0234
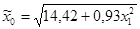
		87,73	3,60	0,0048	8,46	0,0000	71,52	0,0000

Дата добавления: 2015-03-31