Теорема Ферма

Теорема Ферма, - утверждение, что для любого натурального числа n > 2 уравнение xⁿ + yⁿ = zⁿ (уравнение Ферма) не имеет решений в целых ненулевых числах x, y, z. Теорема была сформулирована Пьером Ферма примерно в 1630 году на полях книги Диофанта "Арифметика" следующим образом: "невозможно разложить ни куб на два куба, ни биквадрат на два биквадрата, и вообще никакую степень, большую квадрата, на две степени с тем же показателем". И далее добавил: "я открыл этому поистине чудесное доказательство, но эти поля для него слишком малы". В бумагах Пьера Ферма нашли доказательство теоремы Ферма для n = 4. Нездоровый интерес к доказательству этой теоремы среди неспециалистов в области математики был в свое время вызван большой международной премией, аннулированной в конце первой мировой войны.

Предполагается, что доказательство теоремы Ферма вообще не существовало.

Для n = 3 теорему Ферма доказал Л. Эйлер, для n = 5 И. Дирихле и А. Лежандр, для n = 7 - Г. Ламе. Теорему Ферма достаточно доказать для любого простого показателя n = p > 2, т. е. достаточно доказать, что уравнение

x^p + y^p = z^p (1)

не имеет решений в целых ненулевых взаимно простых числах x, y, z. Можно также считать, что числа x и y взаимно просты с p. При доказательстве теоремы Ферма рассматривают два случая: первый случай, когда (xyz, p) = 1 и второй случай, когда p | z. Доказательство второго случая теоремы Ферма более сложно и обычно проводится методом бесконечного спуска. Существенный вклад в доказательство теоремы Ферма внес Э. Куммер, который создал принципиально новый метод, основанный на разработанной им арифметической теории кругового поля. 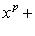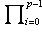Используется тот факт, что в поле , левая часть уравнения (1) разлагается на линейные множители , которые являются p -ми степенями идеальных чисел поля в первом случае и отличаются от p -х степеней на множитель 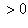во втором случае. Если p делит числители Бернулли чисел B _{2 n} (n = 1, 2,..., (p - 3)/2), то по критерию регулярности p не делит число h классов идеалов поля и эти идеальные числа - главные. В этом случае Э. Куммер доказал теорему Ферма. Не известно бесконечно или конечно число регулярных чисел p (по теореме Иенсена число иррегулярных простых чисел бесконечно). Э. Куммер доказал теорему Ферма для некоторых классов иррегулярных простых чисел и тем самым установил ее справедливость для всех p < 100. В первом случае он показал, что из (1) следует выполнимость сравнений

n = 2, 4,..., p - 3,

справедливых при любой перестановке x, y, - z. Отсюда он получил, что если в первом случае уравнение (1) разрешимо, то для n = 3, 5

(2)

Дата добавления: 2015-03-29