Достаточное условие строгой монотонности функции на промежутке

Необходимое и достаточное условие монотонности функции на промежутке.

Необходимое и достаточное условие постоянства функции на промежутке

Теорема
Пусть функция f(x) определена в промежутке X и имеет внутри него конечную производную f/(x), а на концах (если они принадлежат X) сохраняет непрерывность. Для того чтобы f(x) была в X постоянной, достаточно условие f/(x)=0 внутри X.

Доказательство
Пусть это условие выполнено. Фиксируем некоторую точку x0 из промежутка X и возьмем любую другую его точку x. Для промежутка [х0,х] или [х,х0] удовлетворены все условия теоремы Лагранжа. Следовательно, можем написать

f(x)−f(x0)=f/(c)(x−x0),

где c содержится между x0 и x, а значит, заведомо лежит внутри X. Но, по предположению, f/(c)=0, так что для всех x из X

f(x)=f(x0)=const.

Теорема доказана.

Заметим, что высказанное условие, очевидно, является и необходимым для постоянства функции.

Следствие. Пусть две функции f(x) и g(x) определены в промежутке X и внутри него имеют конечные производные f/(x) и g/(x), а на концах (если они принадлежат X) сохраняют непрерывность. Если при этом f/(x)=g/(x) внутри X,

то во всем промежутке X эти функции разнятся лишь на постоянную:

f(x)=g(x)+C (С = const).

Для доказательства достаточно применить теорему к разности f(x)−g(x), так как ее производная f/(x)−g/(x) внутри X сводится к нулю, то сама разность в X будет постоянной.

Теорема (достаточное условие)

Если функция f(x) дифференцируема на (a,b) и f/(x)≥0 (f/(x)≤0) на (a,b), то f(x) не убывает (не возрастает) на (a,b).

Доказательство
Рассмотрим случай когда f/(x)≥0. Рассмотрим две точки x1,x2∈(a,b) и применим формулу Лагранжа. На [x1,x2] функция f(x) удовлетворяет всем условиям этой теоремы. Следует, чтоx1<x2:

f(x2)−f(x1)=f/(c)(x2−x1), где c∈(x1,x2) и правая часть больше нуля, значит f(x2)−f(x1)≥0 или f(x2)≥f(x1) при x2>x1, функция не убывает.

Теорема доказана.

Замечание

Если требовать, что f/(x)>0 (f/(x)<0), тогда функция строго возрастает (убывает).

6. необходимое условие экстремума.

Необходимый признак существования экстремума:

Для нахождения экстремумов функции z =f (x,y) сначала нужно найти стационарные точки этой функции, в которых частные производные функции z =f (x,y) равны нулю. Для этого нужно решить систему уравнений:

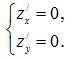(1)

Функция может иметь экстремум также в тех точках, где хотя бы одна из частных производных не существует.

Условие (1) является необходимым условием экстремума, но оно не является достаточным, т.е. в стационарной точке экстремума может и не быть.

Рассмотрим достаточное условие экстремума. Пусть точка M₀ – стационарная точка функции z=f (x,y), которая имеет непрерывные частные производные второго порядка на некоторой окрестности точки M0,

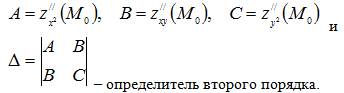
Если D>0, то экстремум в точке M0 есть, при этом M0 – точка минимума при A>0 и M0 – точка максимума при A<0. Если D<0, то экстремума в точке M0 нет.

При D=0 требуются дополнительные исследования функции в окрестности точки M0, мы не будем рассматривать этот случай.

7. достаточное условие экстремума. Смотри в 6 вопросе.

8. направление выпуклости графика функции, точки перегиба графика.

Направление выпуклости графика функции.

Точки перегиба

Дадим определение направления выпуклости графика функции. Предположим, что функция дифференцируема на интервале . Это значит (см. §3), что на данном интервале график функции имеет в каждой своей точке касательную, не параллельную оси ординат.

Определение. Говорят, что график функции имеет на интервале выпуклость, направленную вниз (вверх), если график этой функции в пределах данного интервала лежит выше (ниже) любой своей касательной.

Следующая теорема устанавливает связь между направлением выпуклости графика функции и знаком её второй производной. Эта теорема приводится здесь без доказательства.

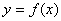Теорема 25.1. Пусть функция имеет на интервале вторую производную. Тогда, если эта производная положительна (отрицательна) всюду на этом интервале, то график функции имеет на интервале выпуклость, направленную вниз (вверх).

Дадим определение точки перегиба. Предположим, что функция дифференцируема на интервале , т.е. в любой точке, абсцисса которой принадлежит интервалу , график этой функции имеет касательную.

Определение. Точка графика функции 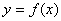называется точкой перегиба этого графика, если существует такая окрестность точки оси абсцисс, в пределах которой график функции 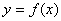слева и справа от точки имеет разные направления выпуклости.

График функции 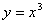, изображённый на рисунке 6, на интервале имеет выпуклость, направленную вверх, на интервале – выпуклость, направленную вниз; точка (0,0) является точкой перегиба этого графика.

Сформулируем без доказательства необходимое условие перегиба графика функции, имеющей вторую производную.

Теорема 25.2. Если функция 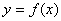имеет в точке вторую производную и график этой функции имеет перегиб в точке , то .

Отсюда ясно, что перегиб следует искать лишь в тех точках оси абсцисс, в которых сама функция дифференцируема, а вторая производная этой функции либо равна нулю, либо не существует. Такие точки называются критическими точками второго рода.

Заметим, что равенство нулю второй производной является необходимым, но не достаточным условием перегиба. Так, например, функция в точке не имеет перегиба, хотя вторая производная этой функции, равная 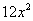, в точке равна нулю.
Сформулируем теперь без доказательства достаточное условие перегиба.

Теорема 25.3. Пусть функция 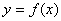имеет вторую производную в некоторой окрестности точки , при этом сама точка является критической точкой второго рода. Тогда, если в пределах указанной окрестности вторая производная 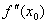имеет разные знаки слева и справа от точки , то график этой функции имеет перегиб в точке .

Пример Найти интервалы, на которых сохраняется определённое направление выпуклости, и точки перегиба графика функции .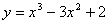

Решение. Найдём критические точки второго рода: , ,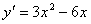

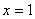при , . Вторая производная существует на всей действительной оси, поэтому других критических точек второго рода нет. При , при 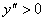, поэтому в интервале график заданной функции имеет выпуклость, направленную вверх, в интервале – выпуклость, направленную вниз, а точка графика (1,0) является точкой перегиба.

Односторонняя непрерывность. Точки разрыва функции, их классификация. Непрерывность функции на отрезке. Свойства непрерывных на отрезке функций: ограниченность, существование наибольшего, наименьшего и всех промежуточных значений. Точки разрыва монотонной функции, их счетность. Критерий непрерывности монотонной функции. Непрерывность обратной функции. Равномерная непрерывность

9. необходимое условие перегиба.

Дата добавления: 2015-03-29