
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Наклонные асимптоты
|
|
|
|
Горизонтальные асимптоты
Если
 ,
,
то у = b — горизонтальная асимптота кривой y = f (x) (правая – при х стремящемуся к плюс бесконечности, левая – при х стремящемуся к минус бесконечности и двусторонняя, если пределы при х стремящемуся к плюс-минус бесконечности равны).
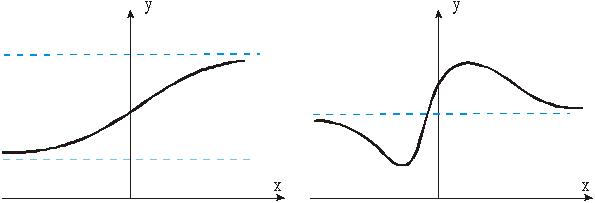
Рис. 8.3. Примеры горизонтальных двухсторонних и односторонних асимптот
Уравнение наклонной асимптоты функции y = f (x) определим уравнением y = k·x + b. При этом параметры наклонной асимптоты определяются соотношениями
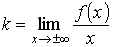 ,
,
 .
.
Для того, чтобы функция y = f (x) имела асимптоту y = k ·x + b, необходимо и достаточно, чтобы существовали указанные выше конечные пределы.
Доказательство. По определению асимптоты имеем
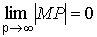 .
.
Так как MP = MP 1·cos α, где угол α есть величина постоянная, равная углу наклона асимптоты к оси Ох. Поэтому соотношение для определения асимптоты можно записать в виде
 .
.
Так как точки М и Р 1 соответствуют одному и тому же значению аргумента, то это соотношение можно записать в виде
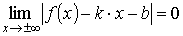 . (9.1)
. (9.1)
Если вынести за скобки х, то
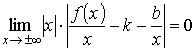 ,
,
из этого однозначно будет следовать
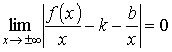 ,
,
или
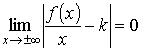 .
.
Откуда следует соотношение для нахождения углового коэффициента асимптоты
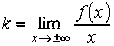 .
.
Зная угловой коэффициент асимптоты, из соотношения (9.1) получим
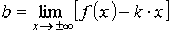 .
.
12. план исследования функции.
- Определение области определения.
- Определение четности или нечетности.
- Определение периодичности функции.
- Определение интервалов знака постоянства первой производной.
- Определение интервалов знака постоянства второй производной.
- Составление таблицы результатов.
| х | |||||||
| у ' | |||||||
| у '' | |||||||
| у |
- В первой строчке таблицы указываются интервалы, на которые разбивается область определения функции точками разрыва, точками экстремума и точками перегиба в порядке следования. Сами эти точки в порядке следования помещаются в отдельные столбцы. Во второй строчке таблицы в каждой ячейке указываются знаки первой производной. В третьей строчке таблицы в каждой ячейке указываются знаки второй производной. В четвёртой строчке определяется характер поведения функции в каждой ячейке. Если это точки экстремума или точки перегиба, то указываются значения функции в этих точках.
- Нахождение асимптот.
- Построение графика функции, начинается с построения асимптот и характерных точек.
|
|
|
|
|
Дата добавления: 2015-03-29; Просмотров: 532; Нарушение авторских прав?; Мы поможем в написании вашей работы!