Доказательство. Множества применений образцов t1 и t2 -Ut1 и Ut2 совпадают тогда и только тогда, когда t1 и t2 совпадают с точностью до переименования переменных

ТЕОРЕМА 9.1

Множества применений образцов t ₁ и t ₂ -U t ₁ и U t ₂ совпадают тогда и только тогда, когда t ₁ и t ₂ совпадают с точностью до переименования переменных.

Необходимость. (Þ) Покажем, что если U t ₁ = U t ₂, то образцы t ₁ и t ₂ совпадают с точностью до переименования переменных.

Пусть U t ₁ = U t ₂. Без ограничения общности можно считать, что множества символов переменных в образцах t ₁ и t ₂ не пересекаются.

Длины слов t ₁ и t ₂ совпадают. Действительно, всякое применение произвольного образца, получаемое заменой символов переменных на слова, состоящие из одного символа, имеет длину, равную длине самого образца. Поэтому если бы длины образцов t ₁ и t ₂ были разными, то множество применений более короткого образца содержало бы слова, не входящие во множество применений другого образца.

Пусть t ₁ = s₁,..., s _k и t ₂ = d₁,..., d _k.

Произведем последовательное посимвольное сравнение t ₁ и t ₂слева направо.

При этом возможны следующие случаи:

1) s _i Î (А 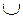B);

2) s _i Î V.

Рассмотрим первый из этих случаев и покажем, что справедливы соотношения d _i Î (А 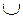B)и s _i = d _i.

Для этого рассмотрим множества всех таких применений t ₁ и t ₂, которые получаются из t ₁ и t ₂ заменой символов переменных на слова длины 1.

Тогда, если d _i s _i, то рассматриваемые множества кратчайших по длине слов в U t ₁ и U t ₂ являются разными, так как i -й символ всех слов первого множества равен s _i. Однако значения i -го символа слов второго множества могут быть отличными от s _i.

Из проведенных рассуждений следует, что на одинаковых позициях образцов t ₁ и t ₂ могут располагаться либо символы переменных, либо равные символы из А 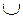B.

Рассмотрим второй случай. Покажем, что в этом случае d _i также является символом переменной и s _i = s _j тогда и только тогда, когда d _i = d _j. Первое из приведенных свойств верно, поскольку если d _i Î А 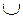B, то в кратчайших применениях t ₂ символ с порядковым номером i всегда равен d _i, а в кратчайших применениях t ₁ символ с тем же номером принимает значения всех символов из А B.

Проверим справедливость второго свойства. Пусть s _i Î V и s _j, j < i,обозначают одну и ту же переменную в t ₁. Тогда все применения t ₁, получаемые заменой переменных на слова длины 1 в алфавите А È B, имеют одинаковые j -й и i -й символы. Если же d _i и d _j - разные символы переменных в t ₂, то среди кратчайших по длине применений образца t ₁ имеются такие, в которых j -й и i -й символы - разные. Поэтому U t ₁ ¹ U t ₂. Последнее заключение противоречит предполагаемому равенству множеств U t ₁ и U t ₂.

Доказательство того, что если d _i = d _j, то s _i = s _j можно провести аналогичными рассуждениями.

Из доказательства свойств, имеющих место в случаях 1 и 2, следует, что t ₁ и t ₁ совпадают с точностью до переименования переменных.

Достаточность. (Ü) Пусть образцы t ₁ и t ₂ совпадают с точностью до переименования переменных. Тогда множества применений этих образцов совпадают.

Действительно, пусть подстановка Q ₁ = 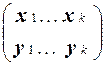задает переименование переменных из t ₁ в переменные из t ₂, которое преобразует t ₁ в t ₂.

Тогда, если слово 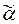является применением t ₁, получаемым с помощью подстановки p, то 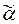является применением t ₂ с помощью подстановки QQ ₁, т.е. U t ₁ Í U t _2. Обратное включение U t ₁ Í U t ₂ доказывается аналогично. Поэтому U t ₁ = U t ₂.

Следовательно, U t ₁ = U t ₂.

Дата добавления: 2015-03-31