Тема № 6 Электричество и магнетизм. Опыт показывает, что между электрически заряженными и намагниченными телами действуют силы, называемые электромагнитными

6.1 Электростатика

Опыт показывает, что между электрически заряженными и намагниченными телами действуют силы, называемые электромагнитными. Относительно природы этих сил в науке выдвигались две противоположные точки зрения. Ранее известная из них исходила из представления о непосредственном действии на расстоянии, без участия каких бы то ни было материальных посредников. Более новая точка зрения, принятая в настоящее время, исходит из представления, что взаимодействия передаются с помощью особого материального посредника, называемого электромагнитным полем. Большой вклад в развитие современной теории поля внесли Фарадей, Максвелла многие другие

Термин электрический заряд используется в физике, во-первых, для названия небольшого заряженного тела. Если размерами тела в данной задаче можно пренебречь, заряд называется точечным, заряд, не искажающий электрическое поле, в которое его вносят, называется пробным. Во-вторых, так называется физическая величина, количественно характеризующая электрические свойства тел. Возьмём два пробных заряда и будем последовательно помещать их в одну и ту же точку электрического поля. Опыт показывает, что силы, действующие на эти заряды напрвлены в одну или прямо противоположные стороны, а отношение их модулей не зависит от положения точки, в которую помещаются эти заряды. По определению, отношение зарядов двух тел равно отношению действующих на них сил

q₁/q₂ = F₁/F₂. (6.1)

При этом тела имеют одинаковые знаки, если действующие на них силы направлены в разные стороны. Основные свойства электрических зарядов: 1) заряды бывают толькодвух видов, - положительные и отрицательные; 2) заряд – дискретная величина, т.е. любой заряд кратен так называемому элементарному электрическому заряду е = 1,60 10^-19 Кл; 3)закон сохранения заряда – полный заряд системы не может измениться, если через её границу не проходят электрически заряженные частицы.

Из формулы (6.1) следует,что

F₁/q₁ = F₂/q₂.

Напряжённость электрического поля Е в данной точке равна отношению силы F, действующей на пробный положительный заряд, помещенный в данную точку, к величине пробного заряда.

Е = F/ q(6.2)

Принцип суперпозиции состоит в том, что напряженность поля, создаваемого системой зарядов, равна векторной сумме напряженностей полей, создаваемых отдельными зарядами.

Основной количественный закон электростатики был открыт Кулоном в 1785 г. Сила взаимодействия двух точечных неподвижных зарядов в вакууме направлена вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов разные, и силой отталкивания, если эти знаки одинаковы.

F₁₂ = С│q₁││q₂│/r₁₂² (6.3)

Коэффициент Св системе единиц СИ равен 9.0 10⁹ Н м²/Кл². В системе СИ коэффициент С принято записывать в виде С = 1/ (4πε₀), где ε₀ = 8,85 10^-12 Ф/м называется электрической постоянной. Напряженность поля точечного заряда q определяется формулой

Е = q/(4πr² ε₀). (6.4)

Так как площадь поверхности сферы S= 4πr², тоформулу (6.4) можно записать в виде

Е S = q/ε₀.

Это соотношение было обобщено Гауссом для произвольной системы электрических зарядов, окружённых замкнутой поверхностью, - поток вектора напряжённости электрического поля через любую замкнутую поверхность пропорционален сумме зарядов, окруженных этой поверхностью.

∮(Е d S) = q/ε₀ (6.5)

Следствием теоремы Гаусса является теорема Ирншоу: всякая равновесная конфигурация покоящихся точечных зарядов неустойчива, если на них, кроме кулоновских сил притяжения и отталкивания, никакие другие силы не действуют. Применим теорему Гаусса для определения напряжённости поля бесконечной равномерно заряженной плоскости. Пусть заряд плоскости положительный с поверхностной плотностью σ, тогда ввиду симметрии задачи вектор Е направлен от плоскости. Построим цилиндр с основаниями площадью S каждое, симметрично расположенными по разные стороны плоскости, и с образующими, перпендикулярными к ней. Тогда поток вектора Е через оба основания равен 2ЕS, а поток вектора Е через боковую поверхность равен нулю. По теореме Гаусса 2ЕS = σS/ε₀, отсюда

Е = σ/ (2ε₀) (6..6)

Простейшей системой электрических зарядов является электрический диполь, - совокупность двух равных по величине, но противоположных по знаку точечных зарядов, расположенных на расстоянии l друг от друга. Если l – радиус-вектор, проведённый от отрицательного заряда к положительному, то вектор р = q l называется электрическим моментом диполя.

Электрическое поле потенциально (консервативно), для таких полей можно ввести понятие разности потенциалов. Разностью потенциалов между двумя точками 1 и 2 электрического поля называется отношение работы сил поля по перемещению пробного положительного заряда q из положения 1 в положение 2 к величине пробного заряда

φ₁ − φ₂ = А₁₂/q (6.7)

Найдём связь разности потенциалов с напряженностью поля.В одномерном случае − dφ=Е_хdх или Е_х = − dφ/dх, аналогичное рассуждение применимо для осей у и z. Тогда в общем виде

Е = − (∂φ/∂х i + ∂φ/∂у j + ∂φ/∂z k)

Так как Е есть вектор, то и выражение, стоящее в скобках, есть также вектор Он называется градиент скаляра φ и обозначается gradφ.. Теперь связь напряжённости и потенциала можно записать так

Е = − grad φ (6.8)

Из связи напряженности и потенциала следует, что единицей напряженности является вольт на метр (В/м)

Земля заряжена отрицательно её электрический заряд испытывает периодические изменения и в среднем составляет 6 10⁵ Кл. Воздух обладает проводимостью, поэтому в атмосфере текут токи, уменьшающие заряд Земли.Внастоящее время можно считать установленным, что заряд Земли поддерживается грозовой активностью атмосферы

Влияние электрического поля на вещество обусловлено тем, что атомы вещества состоят из электронов и положительно заряженных ядер. При внесении тела в поле легкие электроны испытывают смещение против поля, смещение атомных ядер по сравнению с ними пренебрежимо мало, т.е. происходитчастичное разделение зарядов и в отдельных местах тела появляются макроскопические индукционные заряды. Все вещества можно условно разделить на проводники и диэлектрики. Смещение электрических зарядов в проводниках и диэлектриках носит совершенно различный характер. В проводникахносители тока могут легко перемещаться по всему объёму, а в диэлектриках свободных зарядов нет и смещение зарядов ограничено атомными размерами. Электрическое поле в проводниках было подробно исследовано Фарадеем. Им было экспериментально доказано, что напряжённость электрического поля внутри проводника равна нулю. В диэлектриках под действием приложенного электрического поля возникают поляризационные заряды, уменьшающие электрическое поле внутри диэлектрика. Для количественного описания поляризации диэлектрика пользуются вектором поляризации Р, равным дипольному моменту единицы объема диэлектрика. Можно показать, что сумма поляризационных зарядов связана с вектором поляризации соотношением

q_пол = − ∮(Р d S) (6.9)

Поляризационные заряды необходимо добавить в теорему Гаусса

ε₀∮(Е d S) = q − ∮(Р d S) (6.10)

Введём новый вектор D = ε₀ E + P, (6.11)

называемый вектором электрической индукции. Тогда

∮(D d S) = q/ (6/12)

Эта формула называется теоремой Гаусса для электрического поля в диэлектрике. Если среда изотропна, то векторы Р и Е коллениарны и можно записать Р = αε₀ Е,где α- поляризуемость диэлектрика. Связь между векторами D и E записывается в виде

D = ε ε₀ Е, ( 6.13)

где ε = 1 + α называется диэлектрической проницаемость диэлектрика.

Рассмотрим конденсатор, состоящий из двух проводников (обкладок), отделённых друг от друга слоем диэлектрика, заряды на обкладках равны по величине и противоположны по знаку. Плоский воздушный конденсатор состоит из двух плоских пластин площадью S каждая, расположенных на небольшом расстоянии d друг от друга. Напряжённость электрического поля, создаваемого одной пластиной, определяется формулой (6.6) Е₁ = q/(2Sε₀). За пределами конденсатора Е равно нулю, а в промежутке между обкладками Е = 2Е₁

Е = q/(Sε₀)

Отношение заряда конденсатора к разности потенциалов между его обкладками называется ёмкостью конденсатора С. Так как Е = Δφ/d, то

С = ε₀S/d. (6.14)

Если между обкладками расположен диэлектрик с диэлектрической проницаемость ε, то ёмкость конденсатора увеличивается в ε раз

С = εε₀S/d. (6.15)

Энергия электрического поля в конденсаторе Wчисленно равна работе, совершённой при его зарядке

dW = Δφdq = q dq/С,

и после интегрирования получаем

W = q²/2С. (6.16)

Преобразуем это выражение – так как q = СΔφ = С Еd, то

W = εε₀Е²Sd/2. (6.17)

Произведение Sd равно объёму пространства между обкладками, поэтому объёмная плотность энергии электрического поля равна

w = εε₀ Е²/2 = (ЕD)/ 2 (6.18)

В некоторых кристаллах при деформации возникает поляризация, в результате на их поверхностях появляются электрические заряды Это явление получило название прямого пьезоэлектрического эффекта. Существует и обратныйпьезоэффект, - деформация кристалла под действием электрического поля. Эти эффекты имеют широкое техническое применение.

6.2 Постоянный электрический ток

Электрический ток есть упорядоченное движение электрических зарядов, которые называются носителями тока. При известных концентрации n, заряде q и скорости упорядоченного движения u вектор

j = n q u (6.19)

называется плотностью электрического тока. Как показывает опыт, для многих тел плотность тока пропорциональна напряжённости электрического поля

j = λ Е,(6.20)

где λ называется удельной проводимостью, а обратная величина ρ = 1/λ – удельным сопротивлением. Это важное соотношение называется законом Ома в дифференциальной форме.

Рассмотрим важный для практики случай, когда электрические токи текут вдоль тонких проводов. Через поперечное сечение провода S в единицу времени проходит заряд I = jS, называемый силой тока. В замкнутой цепи для поддержания силы тока постоянной должен находится источник тока, в котором действуют силы неэлектрического происхождения, называемые сторонними силамиF^стор. Обозначим F^стор/q = Е^стор, тогда из закона Ома

Е + Е^стор = ρI/S.

Умножим это соотношение на элемент длины провода dl и проинтегрируем по всей цепи

∫Е dl + ∫Е^сторdl = I∫ρ dl/S (6.21)

Первый интеграл равен нулю, т.кк электрическое поле консервативно. Второй интеграл, равный отношению работы сторонних сил по перемещению пробного заряда по всей цепи к величине пробного заряда, называется электродвижущей силой E источника тока. Третий интеграл

R = ∫ρ dl/S (6.22)

называется электрическим сопротивлением. Формула (6.21) теперь записывается в виде

E = I (R + r), (6.23)

Это соотношение называется законом Ома для полной цепи в интегральной форме, где полное сопротивление разделено на сопротивление нагрузки R и внутреннее сопротивление источника тока r.

При расчёте сложных разветвлённых электрических цепей используются правила Кирхгофа: 1) В каждой точке разветвления проводов алгебраическая сумма токов равна нулю; 2) В каждом замкнутом контуре сумма э.д.с. равна сумме напряжений на отдельных участках контура.Э.д.с. считается положительной, если при выбранном направлении обхода контура этот источник проходится от минуса к плюсу. Напряжение на участке берётся положительным, если направление обхода контура совпадает с указанным направлением тока на этом участке

При прохождении через резистор R электрического тока I за время t выделяется количество тепла, определяемого законом Джоуля – Ленца

Q = I² R t (6.24)

6.3 Магнитное поле.

Магниты были известны и использовались человеком очень давно, однако систематическое изучения=е магнетизма началось в ХIХ веке после установления магнитного действия постоянного тока. Закон, определяющий силу, действующую на движущийся со скоростью v точечный заряд q в магнитном полем, получен Лоренцем обобщением опытных фактов

F = q[ v В ], (6.25)

где вектор В характеризует магнитное поля и называется вектором индукции магнитного поля. Его модуль равно отношению максимальной силы Лоренца к произведению qv, а его направление можно определить по ориентации магнитной стрелки, помещённой в данную точку. На линейный элемент тока Id l в магнитном поле действует сила, установленная Ампером

d F = I [ d l В ] (6.25)

Магнитное поле точечного заряда q, двигающегося со скоростью v, определяется выражением

В = С_м q [ v r ]/r³, (6.26)

где r – радиус вектор, проведённый от заряда к точке наблюдения, а множитель С_м в системе СИ равен 10^-7 Г/м, обычно он записывается в виде С_м = μ₀/(4π), где μ₀ = 1,26 10 ^-6 Г/м При магнитном взаимодействии двух электронов, летящих с одинаковыми скоростями v на расстоянии r друг от друга на каждый из них действует сила притяжения

F_м = С_мv² е²/r²,

а сила их кулоновского отталкивания равна

F_к = С е²/r²

Отношение этих сил равно С_м/С_к = v²/с², где с=3 10⁸ м/с – скорость света в вакууме. Это отношение ничтожно и не превышает 10^-20. Однако в переносе тока участвует громадное количество заряженных частиц и это компенсирует малость множителя (v/с)².х

Магнитное поле линейного элемента тока определяется по закону Био и Савара

d B = μ₀ I [d lr ]/ (4π r³) (6.27)

Для очень длинного прямолинейного проводника с током I вычисление интеграла (6.27) даётдля модуля магнитного поля на расстоянии R от провода

В = μ₀ I/(2π R) (6.28)

Направление вектора индукции определяется по правилу буравчика: если вращать буравчик таким образом, чтобы он перемешался в направлении тока в проводнике, то направление движения рукоятки буравчика определяет направление вектора индукции магнитного поля. Так как l = 2πR определяет длину окружности, то В l = μ₀ I. Это равенство, как оказывает внимательное рассмотрение, может быть обобщено на произвольный случай. В результате получается теорема о магнитной циркуляции: циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме токов, пронизывающих контур циркуляции.

∮(В d l) = μ₀ I. (6.29)

Ток в сумме токов I считается положительны м, если его направление совпадает с направлением движения буравчика, рукоятка которого двигается по напрвлению обхода контура.

Теорема Гаусса для магнитных полей имеет вид

∮ (В d S) = 0 (6.30)

Тот факт, что справа стоит нуль, говорит о том, что магнитных зарядов не существует.

В веществе магнитное поле возбуждается не только токами проводимости, но и движениями заряженных частиц внутри самих атомов и молекул. В основном всё определяется движением электронов, т.к. тяжелые ядра двигаются гораздо медленнее легких электронов Из-за хаотичности теплового движения при отсутствии внешнего магнитного поля атомы вещества ориентированы хаотически и возбуждаемые ими поля компенсируют друг друга. При наложении внешнего поля такая компенсация нарушается. Микроскопические молекулярные токи при этом создаю макроскопические токи намагничивания. В теореме о магнитной циркуляции необходимо учесть токи намагничивания

∮(В d l) = μ₀ (I + I_м) (6.31)

Намагниченность принято характеризовать вектором намагничивания I, равным магнитному моменту единицы объёма магнетика.. Можно показать, что связь токов намагничивания с вектором намагничивания имеет вид

I_м = ∮(I d l).

Введём вспомогательный вектор

Н = В /μ₀ ─ I (6.32)

Тогда теорема о магнитной циркуляции в веществе примет вид

∮(Н d l) = I (6.33)

Для слабых магнетиков связь между I и Н линейная, т.е. I = æ Н, отсюда

В = μμ₀ Н. (6.34)

Величина æ называется магнитной восприимчивостью, μ = 1 + æ, - магнитной проницаемостью вещества. Если μ > 1, то среда называется парамагнетиком, если μ < 1, тела называется диамагнетиком.

Железо и все так называемые ферромагнитные вещества обладают сильными магнитными свойствами, нелинейной зависимостью между вектором намагничивания и вектором В, а также

Магнитным гистерезисом, т.е. зависимостью намагничивания от предистории. Ферромагнетики сохраняют свои свойства только в промежутке между двумя температурами Кюри.

6.4 Электромагнитная индукция.

Открытие в 1831 г. Фарадеем явления электромагнитной индукции было одним из важнейших в электродинамике. Явление состоит в появлении индукционного токапри любых изменениях магнитного потока Ф = ∫(В d S). Основной закон электромагнитной индукции имеет вид

E_i = ─ dФ/dt (6.35)

Формула (6.35) определяет не только величину, но и направление индукционного тока. По правилу Ленца индукционный ток всегда имеет такое направление, чтобы он ослаблял действие причины, возбуждающей этот ток. Это правило было обобщено в принципе ЛеШателье–Брауна на все физические явления. Максвелл по-другому трактовал явление электромагнитной индукции. В его формулировке всякое изменение магнитного поля во времени возбуждает в окружающем пространстве электрическое поле

∮(Е d l) = ─ ∫(∂ В /∂td S). (6.36)

Полученное уравнение входит в число знаменитых уравнений Максвелла.

Рассмотрим тонкий замкнутый провод, по которому течет ток I, пусть В – индукция магнитного поля этого тока, а Ф – магнитный поток. Обычно магнитный поток пропорционален току

Ф = L I (6.37)

Коэффициент L называется коэффициентом самоиндукции или индуктивностью контура. Рассмотрим катушку длиной l, на которую равномерно намотано N витков тонкого провода, называемую соленоидом. Если S – площадь одного витка, то индукция магнитного поля внутри соленоида равна

В = μμ₀ IN/l,

магнитный поток

Ф = μμ₀ IN²S/l.

Тогда индуктивность соленоида

L = μμ₀ N²S/l. (6.38)

Энергия магнитного поля внутри соленоида равна

W = LI²/2 = Ф²/(2L) = В²Sl/(2μμ₀).

Так как Sl = V – объём соленоида, то объёмная плотность энергии магнитного поля равна

W = В²/(2μμ₀) = (В Н)/2 (6.39)

Важнейшим применением явления электромагнитной индукции является получение переменного тока. При вращении замкнутой рамки в магнитном поле в этой рамке возникает переменный ток с частотой, равной частоте вращения рамки. Из практических соображений в генераторе переменного тока в статоре расположены три рамки, сдвинутые друг относительно друга на 120⁰, внутри которых вращается постоянный электромагнит. Сила тока в каждой рамке изменяется по гармоническому закону

I = I₀cos (ωt) (6/40)

Мгновенная мощность тока на резисторе сопротивлением R равна

Р = I²R = I₀²R cos²(ωt) = I₀²R(1 + cos (ωt))/2 (6/41)

Средняя мощностьполучается при усреднении (6.41). Среднее значение синуса и косинуса за достаточно большой промежуток времени равно нулю, поэтому среднее значение мощности переменного тока определяется выражением

Р^* = I₀²R/2 (6.42)

В электротехнике используется эффективное значение силы тока I_эфф(и напряжения), которое в√2 раз меньше амплитудного значения I₀, при этом формула для мощности такая же, как и для постоянного тока

Р^* = I_эфф² R. (6.42)

Сопротивление элементов цепи переменного тока Z определяется как отношение амплитудных значений тока и напряжения. Можно показать, что сопротивления основных элементов радиотехнических схем определяются выражениями: Z_R = R; Z_L = ωL; Z_С = 1/(ωС).Общее сопротивление последовательно соединенных резистора, конденсатора и катушки индуктивности определяется формулой

Z = √(R² + (ωL ─ 1/(ωС))²) (6.43)

Величина Z играет роль сопротивления в законеОма для переменного тока.

При передаче переменного тока на большие расстояния используется высокое напряжение. Это делается дляуменьшение потерь в передающих переменный ток линий электропередач, мощность которых определяются формулой

Р_пот = Р²ρl/(U²S)

где Р – передаваемая мощность, U – напряжение, l и S – длина и площадь сечения проводов. Уменьшение потерь за счёт увеличения S, но это связано с увеличением массы проводов и практически не применимо.

Определим мощшость в цепи переменного тока вобщем случае. Если напряжение сдвинуто по фазе относительно тока на угол E, то мгновенная мощность равна I₀U₀cos(ωt) cos(ωt─δ).откуда по известной тригонометрической формуле

Р = I₀U₀/2 ((cos(2ωt ─δ) + cos δ)

При усреднении этого выражения получается

Р* = I₀U₀cosδ /2 (6/44)

6.4 Уравнения Максвелла

Основные уравнения электродинамики были установлены Максвеллом в начале 60-х годов ХIХ века. Далеко не все законы и уравнения, входящие в систему уравнений Максвелла, получены самим Максвеллом, его заслуга состоит в том, что он собрал основные уравнения электродинамики в стройную систему и сих помощью решил целый ряд вопросов. Максвелл обобщил и дополнил теорему о магнитной циркуляции (6.33). К необходимости такого обобщения можно прийти при рассмотрении такого примера. Пусть в неограниченную проводящую среду помещен заряженный шар. От этого шара врадиальныхнаправлениях возникнут электрические токи, которые должны возбуждать магнитное поле В. Магнитное поле не может иметь радиальной составляющей, а составляющие, перпендикулярные радиусу, тоже должна быть нулю т.к. среда изотропна. Таким образом В должно равняться нулю, значит токи проводимости, - не единственная причина возникновения магнитного поля. Эту причину Максвелл назвал током смещения I_см, а сумму I + I_см - полным током. Значение тока смещения определяется условием I + I_см = 0, I = - dQ/dt, а потому по теореме Гаусса

I_см = ∫(∂ D /∂td S)

Запишем теперь полную систему уравнений Максвелла

∮(Н d l) = I + ∫(∂ D /∂t d S) (6.45)

∮(Е d l) = ─ ∫(∂ В /∂t d S) (6.46

∮(D d S) (6.47)

∮(В d S) = 0 (6.48)

D = εε₀ Е (6.49)

В = μμ₀ Н (6.50)

j = λ Е (6.51)

Из уравнений Максвелла следует существование электромагнитных волн.

При распространении одномерного возмущения вдоль оси Х со скоростью v смещение описывается формулой

S = f(х ─ vt) (6.52)

Непосредственным дифференцированием можно убедится в том, смещение удовлетворяет дифференциальному уравнению

∂²s/∂х² ─ 1/v² ∂²s/∂t² = 0, (6.53)

которое называют волновым уравнением. Как было показано Максвеллом, изменения векторов Е и Н в плоской электромагнитной волне описываются таким же волновым уравнением, скорость электромагнитной волны определяется формулой

v² 1/(εε₀μμ₀) (6.54)

Вычисления по этой формуле в случае вакуума даю значение скорости, совпадающее со скоростью света в вакууме с = 3,0 10⁸ м/с. Простейшей системой, излучающей электромагнитные волны, является диполь Герца, представляющий собой точечный диполь, дипольный момент которого быстро изменяется во времени. Как показали расчёты, произведенные Герцем, мощность излучения диполя пропорциональна четвёртой степени частоты ω. Мощность излучения движущегося одиночного заряда пропорциональна квадрату его ускорения, т.е. равномерно движущийся заряд электромагнитных волн не излучает.

Уравнения Максвелла необходимо дополнить соотношениями, определяющими энергию электромагнитной волны, плотность потока энергии определяется вектором Пойнтинга

S = [ ЕН ] (6.55)

Дальнейшие исследования показали, что целый ряд явлений является электромагнитными волнами, которые отличаются друг отдруга частотой. В шкалу электромагнитных волн входят (в порядке возрастания частоты) радиоволны, инфракрасное излучение, видимое излучение, ультрафиолетовое излучение, рентгеновское излучение, γ-излучение. Важное место в современной жизни занимают радиоволны. При излучении и приёме радиоволн широко используются колебательные контуры, - системы состоящие из последовательно соединённых конденсатора С, катушки индуктивности L и резистора R, к которым подсоединён источник с переменной электродвижущей силой E. Процессы, происходящие в контуре, описываются уравнением

L 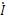+ RI + q/С = E.

Так как I = 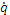, то уравнение запишется в видеγ

L + R 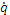+ q/С = 0. (6.56)

При свободных (E = 0) колебаниях в идеальном контуре (R = 0) собственная частота контура равна

ω₀ = 1/√L͞С (6.57)

Введём обозначения R//(2L) = γ, 1/(LС) = ω₀², E/С = Х., тогда уравнение (6.56) примет вид

+ 2γ 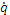+ ω₀²q = 0 (6/58)

Для его решения введём новую переменную у, полагая q = у exp(─γt)

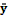(ω₀² ─ γ²) у = 0.

Введём обозначение ω² = ω₀² ─ γ², тогда (6.59)

q = q₀exp(─γt) cos(ωt + δ) (6.60)

Это уравнение описывает затухающие колебания в контуре, собственная частота определяется формулой (6.59)

Рассмотрим вынужденные колебания в контуре под действием синусоидальной силы E/С =Х = Х₀cos (ωt).

Уравнение колебаний имеет вид

+ 2γ 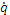+ ω₀²q = X (6.61)

Сразу отметим, что вынужденные колебания происходят с частотой вынуждающей силы, поэтому решение будем искать в виде

q = А(ω) cos(ωt ─δ) (6.62)

Можно показать, что

А(ω) = Х₀/((ω₀² – ω²)² + 4ω²γ²)^1/2 (6.63)

tgE = 2ωγ/ (ω₀² – ω²)^1/2 (6.64)

Как видно из (6.63), при ω = ω₀ амплитуда вынужденных колебаний максимальна. Явление резкого возрастания амплитуды вынужденных колебаний называется резонансом. Резонанс наступает, когда частота вынуждающей силы близка к частоте собственных колебаний системы.

Дата добавления: 2015-03-31