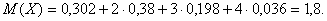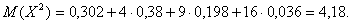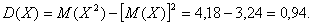КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
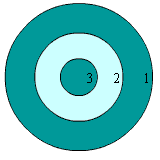
Пример 2. Найти закон распределения числа очков, которые выбивает стрелок на мишени, если вероятность его попадания в область 1 равна 0
Пример 1
|
Найти закон распределения числа очков, которые выбивает стрелок на мишени, если вероятность его попадания в область 1 равна 0, вероятность попадания в область 2 равна 0,2, а в область 3 – 0,8.
Решение
Закон распределения можно представить в виде следующей таблицы:
|
Пусть в мишень стреляют два стрелка. При этом закон распределения числа выбиваемых на мишени очков для первого стрелка задан таблицей:
| 0,2 | 0,8 |
Аналогичный закон распределения для второго стрелка задан таблицей:
| 0,2 | 0,5 | 0,3 |
Найдём закон распределения суммы очков, выбиваемых обоими стрелками.
Составим таблицу – закон распределения случайной величины x + y, где x – количество очков, выбиваемых первым стрелком, а y – количество очков, выбиваемых вторым стрелком.
| ||||||||||||||||||||||||||||||||||||||||||||||||||
Значит, искомое распределение вероятностей задаётся таблицей
| 0,04 | 0,1 + 0,16 = 0,26 | 0,06 + 0,4 = 0,46 | 0,24 |
ая те или иные значения с определёнными вероятностями.
| Закон распределения случайной величины 000246 |
| Автор Administrator | ||||||||||||||||||
| 18.06.2008 г. | ||||||||||||||||||
Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа каждого из приборов равны соответственно р1=0,3; p2=0,4; p3=0,5; p4=0,6. Найти закон распределения этой случайной величины, математическое ожидание и дисперсию числа отказавших приборов. Решение Принимая за случайную величину число отказавших приборов, видим что эта случайная величина может принимать значения 0, 1, 2, 3 или 4. Для составления закона распределения этой случайной величины необходимо определить соответствующие вероятности. Примем 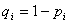 . 1) Не отказал ни один прибор. . 1) Не отказал ни один прибор. 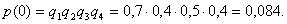 2) Отказал один из приборов. 2) Отказал один из приборов.  0,302. 3) Отказали два прибора. 0,302. 3) Отказали два прибора. 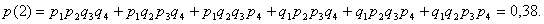 4) Отказали три прибора. 4) Отказали три прибора.  5) Отказали все приборы. 5) Отказали все приборы. 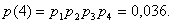 Получаем закон распределения: Получаем закон распределения:
|
Определение 17. Функцией распределения случайной величины X называ-
ется функция F(x), выражающая для каждого x вероятность того, что
случайная величина X примет значение, меньшее x
F(x) = P(X < x). (8.1)
Функция F(x) называется также интегральной функцией распределения
или интегральным законом распределения.
Геометрически функция распределения интерпретируется как вероятность
того, что случайная точка X попадет левее заданной точки x.
Пример
Дано распределение случайной величины
X 1 4 5 7
p 0.4 0.1 0.3 0.2
Найти и изобразить графически ее функцию распределения.
Решение.
Будем задавать различные значения x и находить для них F(x) = P(X < x)
1. Если x 6 1, то F(x) = 0 (в этом случае и при x = 1: F(1) = P(x <
1) = 0
2. Пусть 1 < x 6 4 (например, x = 2);
F(x) = P(X = 1) = 0.4.
Очевидно, что и F(4) = P(X < 4) = 0.4.
3. Пусть 4 < x 6 5 (например, x = 4.25);
F(x) = P(X < x) = P(X = 1) + P(X = 4) = 0.4 + 0.1 = 0.5.
Очевидно, что и F(5) = 0.5.
4. Пусть 5 < x 6 7 (например, x = 5.5);
F(x) = P(X < x) = P(X = 1) + P(X = 4) +
+ P(X = 5) = 0.4 + 0.1 + 0.3 = 0.8.
Очевидно, что и F(7) = 0.8.8.1. Функция распределения случайной величины 61
5. Пусть x > 7;
F(x) = P(X < x) = P(X = 1) + P(X = 4) +
+ P(X = 5) + P(X = 7) = 0.4 + 0.1 + 0.3 + 0.2 = 1.
Изобразим функцию F(x)
При подходе слева к точкам разрыва функция сохраняет свое значение
(функция непрерывна слева). Эти точки на графике выделены.
|
|
Дата добавления: 2015-04-23; Просмотров: 2378; Нарушение авторских прав?; Мы поможем в написании вашей работы!