Ется производная ее функции распределения

Плотностью вероятности (плотностью распределения

или просто плотностью) ϕ(x) непрерывной случайной величины X называ-

ϕ(x) = F (x)

Математическое ожидание M_x случайной величины x равно

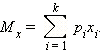
Дисперсией случайной величины x называется среднее значение квадрата отклонения случайной величины от её математического ожидания

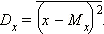
8) Неидеальность передаточной характеристики измерительного устройства причислена к причинам возникнове­ния систематической погрешности. Под передаточной характе­ристикой мы понимаем математическое выражение, описывающее взаимосвязь входной и выходной величин.

Передаточной характеристикой линейного измерительного при­бора, используемого для определения неизменяющихся по вре­мени величин, является константа. В приборах с нелинейной характеристикой зависимость между выходной и входной вели­чинами описывается алгебраическим или трансцендентным урав­нением. В этих случаях погрешности зависят только от размера измеряемого значения и не являются функциями времени.

Это статические погрешности измерения.

При измерении изменяющейся во времени физической вели­чины связь между входной и выходной величинами описывается

дифференциальным уравнением. Возникающие при этом погреш­ности зависят не только от размера измеряемой величины, но и от характера изменения ее во времени. Поэтому их называют динамическими погрешностями.

Так, неизменная во времени температура может быть изме­рена термометром «безошибочно», в то время как быстрые изме­нения температуры из-за его запаздывания отслеживаются не­точно.

Как следует из обобщенной блок-схемы (см. рис. 1.2—1), в показание измерительного устройства преобразуется не только измеряемая величина, но также и внешние влияющие величины. При описании возникающих при этом погрешностей следует раз­личать статические и динамические погрешности.

Строго говоря, статические погрешности можно рассматривать как частный случай динамических. Они полностью содержатся в математическом описании последних. Однако с точки зрения практического применения весьма часто встречающееся измерение постоянных или квазипостоянных величин целесообразно рас­сматривать раздельно, так как методы описания при этом особенно просты.

9) Но́ниус — вспомогательная шкала, устанавливаемая на различных измерительных приборах и инструментах, служащая для более точного определения количества долей делений. Принцип работы шкалы основан на том факте, что глаз гораздо точнее замечает совпадение делений, чем определяет относительное расположение одного деления между другими.

Шкала нониус обычно имеет те же 10 делений, что и основная шкала, а по длине равна только 9 её делениям.

Дата добавления: 2015-04-23