Непараметрические методы оценки корреляционной связи показателей.

Виды взаимосвязи показателей.

Статистические показатели отображают взаимозависимость отдельных сторон изучаемых явлений, могут состоять между собой в следующих основных видах связи:

1Балансовая – характеризует зависимость между источниками формирования ресурсов и их использованием (балансовое равенство).

2Компонентная – характеризуется тем, что изменения статистического показателя определяется изменением отдельных компонентов, входящих в этот показатель в качестве сомножителей.

3Факторная – характеризуется тем, что она проявляется в согласованной вариации изучаемых показателей при этом одни показатели выступают в качестве результативных, а другие в качестве факторных (оказывающих влияние).

Факторные связи подразделяются на функциональные и корреляционные. Функциональные связи (f(x)) определяются влиянием факторного признака на результативный признак (у) полностью по правилу f. Если же влияние на результативный признак (у) обусловлено не всецело, а лишь частично, за счет влияния случайных факторов, то данная форма связи называется корреляционной.

При функциональных связях влияние признаков х и у имеет одинаковую силу для всей совокупности. Поэтому установив зависимость между одной парой xi и yi эту зависимость распространяют на всю изучаемую совокупность. Прогноз при этом имеет абсолютно точное значение. При корреляционной связи значение факторного признака оказывает влияние на признак результативный, который, в свою очередь, принимает различные значения, что определяется влиянием других факторов. Поэтому для изучения такой совокупности в целом устанавливается соотношение, в котором определенному изменению факторного признака соответствует среднее изменение признака результативного.

При изучении корреляционной связи ставятся следующие задачи:

1Проверка экономической теории о возможности связи и придание выявленной связи аналитической формы зависимости.

2Установить количественную оценку тесноты связи.

Непараметрические методы оценки применяются для количественного описания социальных процессов. Они позволяют регистрировать количественные и качественные факторы.

1При исследовании тесноты связи между качественными показателями применяется таблица альтернативных признаков 2х2.

А/В	Да	Нет
Да	a	b	a+b
Нет	c	d	c+d

Для оценки тесноты связи между признаками А и В рассчитывается ряд коэффициентов:

1Коэффициент ассоциации Юла.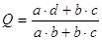

Найденное значение коэффициента, которое изменяется (-1;+1) сравнивается со шкалой Чеддока для того, что бы перейти от количественной оценки к качественной.

При значении коэффициента =0 связь между показателями отсутствует. При значении +1 – связь функциональная. При отрицательном значении связь обратная, а характер связи по силе взаимодействия соответствует шкале Чеддока.

Если в таблице альтернативных признаков отсутствует какое-либо значение, то связь между А и В согласно коэффициенту ассоциации, который в этом случае равен +1 – функциональная, что существенно искажает оценку частоты связи, в этом случае применяется коэффициент контингенции Пирсона:

2Каждый из качественных признаков состоит более чем из двух групп, в этом случае для оценки частоты связи применяют коэффициент сопряженности Пирсона-Чупрова:

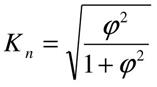
3Для определения тесноты связи как между качественными, так и между количественными признаками при условии что значение этих признаков могут быть упорядоченными или проранжированными по степени возрастания или убывания может быть использован коэффициент ранга Спирмена:

di2 – разница между рангами у и х.

n – число наблюдений или число пар рангов.

Дата добавления: 2015-04-23