Построить модель заданного физического процесса и реализовать ее на компьютере. Проанализировать полученный результат

Построим модель естественного радиоактивного распада ядер [1].

Сформулируем физическую задачу. Ядра распадаются, выбрасывая частицы и превращаясь в более легкие. Распад ядра происходит спонтанно и не зависит от внешних условий. Число распадов, регистрируемых в единицу времени, зависит только от количества атомов, ядра которых способны распадаться. Вероятность распада ядра определяется его устройством и может быть описана некоторым числом, характерным для данных ядер.

Можно сформулировать следующие вопросы:

· Как меняется со временем число ядер?

· Через какое время распадается половина ядер?

Построим математическую модель. На небольшом интервале времени 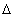t число распавшихся ядер
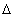– N = N (t) – N (t + 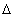t) пропорционально 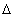t и числу не распавшихся ядер в данный момент N:

,

— здесь 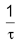— это некоторый коэффициент пропорциональности, определяемый веществом.

Для решения задачи нужно задать количество ядер вещества в начальный момент t = 0: N = N ₀.

Выберем в качестве единицы времени t и 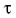представим размерное время , здесь 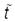— безразмерное время. В качестве характерного числа атомов выберем N ₀, т.е. 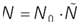, здесь 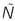показывает долю ядер от их числа в начальный момент. Подставляя размерные величины в исходную систему, получим безразмерные уравнения

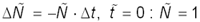
Все величины, входящие в систему, безразмерные, и знак безразмерной величины можно не употреблять.

Составим алгоритм решения нашей системы.

Так как 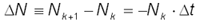, получим рекуррентное соотношение для числа не распавшихся ядер в моменты времени :

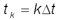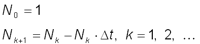
Проведем численный эксперимент в MS Excel. Заполним заголовок таблицы и столбец А, который обозначает номер k, внесем начальное условие и зададим t = 0,1.

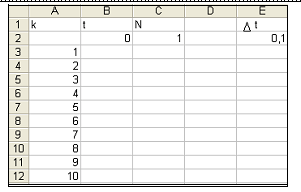
В ячейку В3 внесем формулу для подсчета времени 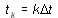и распространим ее на блок В4:В12.

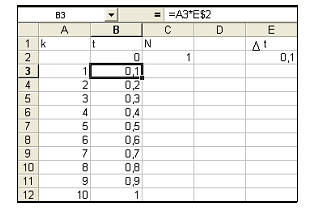
В ячейку С3 внесем рекуррентное соотношение для подсчета N и скопируем его в блок С4:С12.

В столбце В получено время, в столбце С — число ядер. Изобразим эту зависимость на графике:

Для ответа на второй вопрос, который был поставлен в начале задачи, нужно определить момент времени T, за которое распадается половина ядер. Время можно определить из уравнения
N (Т) = 0,5.

Проведем эксперимент с различными значениями 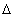t,результаты поместим в таблицу:

Значение времени Т стабилизировалось с точностью 0,001, определено время полураспада ядер Т = 0,693. Полученные в результате эксперимента результаты являются универсальными, так как безразмерная система уравнений не содержит характеристик вещества. Индивидуальность ядер проявляется лишь через масштаб времени .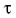

Варианты заданий

1. Составить модель броуновского движения.

2. Составить модель падения тела с учетом сопротивления среды.

Литература

1. Бирих Р.В., Еремин Е.А., Чернатынский В.И. Компьютерные модели в школьном курсе физики. // Информатика № 14, 2006, с. 1–45.

2. Бирих Р.В., Еремин Е.А., Чернатынский В.И. Компьютерные модели в школьном курсе физики. // Информатика № 15, 2006, с. 3–14.

3. Шестаков А.П. Компьютерное математическое моделирование. Лекция № 2. Моделирование в естественных науках. Несколько классических моделей физики. // Информатика № 36, 2002, с. 7–14.

4. Шестаков А.П. Компьютерное математическое моделирование. Лекция № 3. Моделирование в естественных науках. Несколько классических моделей физики. // Информатика № 38, 2002, с. 8–15.

5. Могилев А.В., Пак Н.И., Хеннер Е.К. Информатика: Учебное пособие для педагогических вузов / Под ред. Е.К. Хеннера. М.: Академия, 2004, 848 с.

Дата добавления: 2015-04-23