Решение. С помощью электронной таблицы решить задачу табулирования заданной функции

С помощью электронной таблицы решить задачу табулирования заданной функции. Результат представить в табличной и графической форме.

Программные и аппаратные средства для решения различных профессиональных задач

Этот пункт уже рассмотрен при классификации прикладного программного обеспечения в категории Программы профессионального уровня.

Литература

1. Могилев А.В., Пак Н.И., Хеннер Е.К. Информатика: Учебное пособие для педагогических вузов / Под ред. Е.К. Хеннера. М.: Академия, 2004, 848 с.

2. Олифер В.Г., Олифер Н.А. Сетевые операционные системы. СПб.: Питер, 2001, 554 с.

3. Шалин П. Энциклопедия Windows XP. СПб.: Питер, 2002, 668 с.

Задание

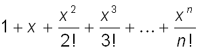; n = 6, x изменяется от 1 до 2 с шагом 0,1.

Для упрощения расчетов преобразуем формулу. Можно применить следующее рекуррентное соотношение для подсчета очередного члена суммы:

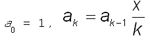, здесь k = 1, 2, …, n

Приступим к заполнению электронной таблицы. Внесем исходные данные. В столбец А внесем значение переменной х от 1 до 2 с шагом 0,1, используя автозаполнение. В строку 2 внесем значения переменной k, также используя автозаполнение. Получим следующую таблицу

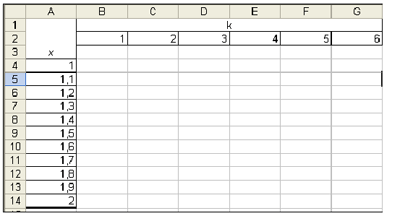
В строку 3 внесем подписи, которые означают очередной член суммы. Далее в столбец В скопируем значения переменной х из столбца А:

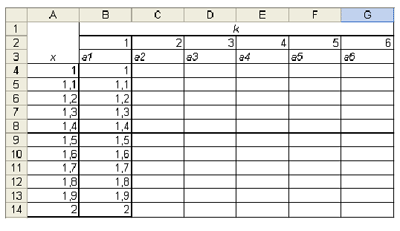
Теперь можно в ячейку C4 внести рекуррентное соотношение, которое позволит вычислить a ₂:

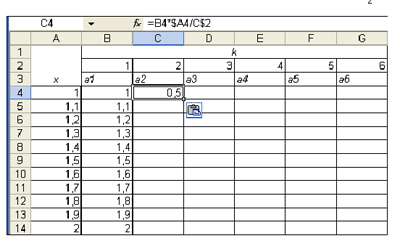
В этом выражении использовалась абсолютная адресация ячейки $A4 для того, чтобы имя столбца А не изменялось при распространении формулы вдоль строки, аналогично абсолютная адресация ячейки C$2 означает, что при копировании формулы вдоль столбца не будет меняться номер строки 2.

Выражение из ячейки С4 можно распространить на блок ячеек D4:G4. Таким образом, в блоке B4:G4 будут получены все слагаемые суммы для начального значения х = 1, кроме единицы.

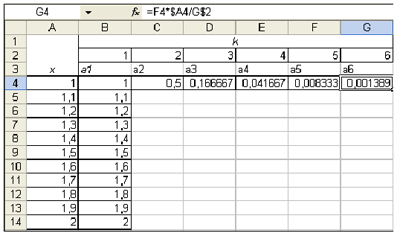
Все готово, чтобы вычислить сумму для начального значения х = 1. Посчитаем ее в ячейке К4.
К сумме добавлена единица, т.к. нулевой член ряда, равный единице для любого значения x, не вычисляется в таблице.

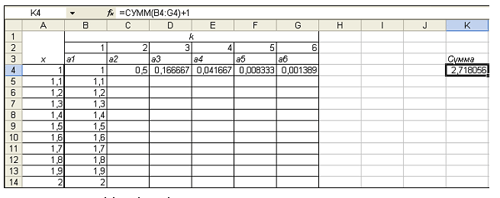
Столбцы H, I, J остались пустыми для того, чтобы можно было увеличить значение n до 9. Распространяя блок ячеек C4:K4 на блок C4:K14, получим результат:

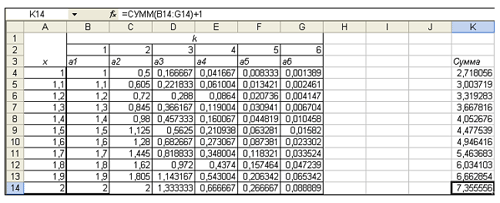
В этой таблице можно увеличить диапазон изменения переменной х. Для этого нужно выделить блок A4:K14 и распространить его на большие значения х.

Используя мастер диаграмм, построим график функции. Вызываем мастер диаграмм и выбираем точечную диаграмму:

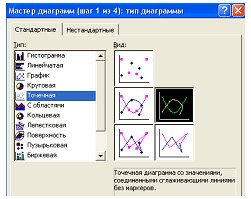
Далее укажем диапазон исходных данных, его образуют два блока — А4:А14 и К4:К14, и получим график:

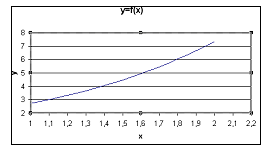
Варианты заданий

С помощью электронной таблицы решить задачу табулирования заданной функции. Результат представить в табличной и графической форме.

1. 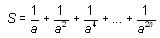, натуральное число n = 5, действительное число a изменяется от 1 до 2 с шагом 0,1.

2. 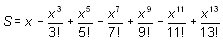, действительное число x изменяется от 1 до 2 с шагом 0,1.

3. 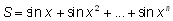, натуральное число n = 6, действительное число x изменяется от 1 до 2 с шагом 0,1.

4. 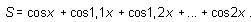, действительное число x изменяется от 2 до 3 с шагом 0,1.

5. 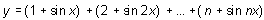, натуральное число n = 6, действительное число x изменяется от 2 до 3 с шагом 0,1.

Дата добавления: 2015-04-23