Параллельность прямой и плоскости. Признак параллельности прямых и плоскости

Общий признак параллельности прямой и плоскости:

прямая параллельна плоскости, если она параллельна какой либо прямой этой плоскости.

Общий признак параллельности плоскостей:

если две пересекающиеся прямые одной плоскости па­раллельны двум пересекающимся прямым другой плос­кости, то эти плоскости параллельны между собой.

Применение этих признаков рассмотрим на примерах решения двух задач.

Задача 1. Через точку К провести плоскость, параллельную прямой m (рис.20)

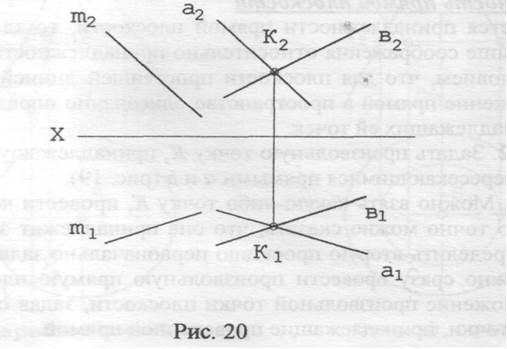
Краткую запись решения задачи 1 можно представить так.

Дано: m (m₁, m₂), К (К_1, К₂)

Провести: Σ // m ^ Σ 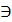К

Решение:

1. Σ(а 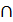b) => а 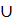Σ ^ b 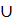Σ => а₁ 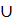Σ₁ ^ b₁ 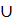Σ₁ =>а₂ 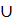Σ₂ ^ b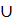₂ Σ₂

2. m // Σ => m // а 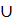Σ => а₁ // m₁ ^ а₂ // m₂

3. b - произвольно, решений - .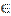

Задача 2. Через точку К провести плоскость Σ, параллельную плоскости Г(n 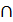m)(рис.21).

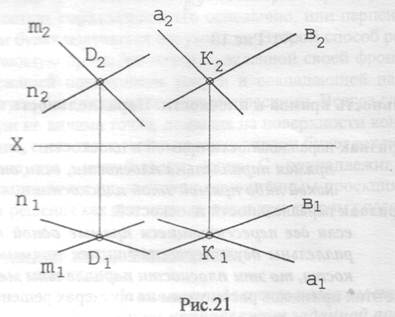
Краткая запись решения задачи 2 выглядит следующим образом.

Дано: Г (n 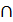m), m (m₁, m₂), n (n₁, n₂), К (К_1,К₂)

Провести: Σ // Г ^ Σ 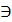К.

Решение:

1. Σ(а 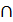b) => а 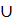Σ ^ b 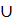Σ => а₁ 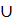Σ₁ ^ b₁ 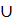Σ₁ =>а₂ 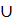Σ₂ ^ b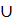₂ Σ₂

2. Σ // Г => а // m ^ b // n 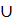Σ => а₁ // m₁ ^ а₂ // m₂ ^ b₁ // n₁ ^ b₂ // n₂

Решение - единственное.

3. Параллельность плоскостей. Признак параллельности плоскостей.

Определение. Две плоскости называются параллельными, если они не пересекаются, сколько бы мы их не продолжали.
Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

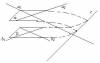
Доказательство. Пусть  и  - данные плоскости, а₁ и а₂ – прямые в плоскости , пересекающиеся в точке А, b₁ и b₂ соответственно параллельные им прямые в плоскости . Допустим, что плоскости  и  не параллельны, то есть они пересекаются по некоторой прямой с. Прямая а ₁ параллельна прямой b ₁, значит она параллельна и самой плоскости . Прямая а ₂ параллельна прямой b₂, значит она параллельна и самой плоскости  (признак параллельности прямой и плоскости). Прямая с принадлежит плоскости , значит хотя бы одна из прямых а₁ или а₂ пересекает прямую с, то есть имеет с ней общую точку. Но прямая с также принадлежит и плоскости , значит, пересекая прямую с, прямая а₁ или а₂ пересекает плоскость , чего быть не может, так как прямые а₁ и а₂ параллельны плоскости . Из этого следует, что плоскости  и  не пересекаются, то есть они параллельны.

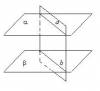
Теорема 1. Если две параллельные плоскости пересекаются третей, то прямые пересечения параллельны.
Доказательство. Пусть  и  - параллельные плоскости, а  - плоскость, пересекающая их. Плоскость  пересеклась с плоскостью  по прямой а. Плоскость  пересеклась с плоскостью  по прямой b. Линии пересечения а и b лежат в одной плоскости  и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.

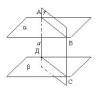
Теорема 2. Отрезки параллельных прямых, заключенных между двумя параллельными плоскостями, равны.
Доказательство. Пусть  и  - параллельные плоскости, а а и b – параллельные прямые, пересекающие их. Через прямые а и b проведем плоскость  (эти прямые параллельны, значит определяют плоскость, причем только одну). Плоскость  пересеклась с плоскостью  по прямой АВ. Плоскость  пересеклась с плоскостью  по прямой СД. По предыдущей теореме прямая с параллельна прямой d. Прямые а, b, АВиСД принадлежат плоскости .Четырехугольник, ограниченный этими прямыми,есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть АД=ВС.

4. Взаимное расположение прямых в пространстве. Параллельные прямые.

Дата добавления: 2015-04-23