Взаимное расположение прямых в пространстве

Параллельность прямых в пространстве. Признаки скрещивающихся прямых

Существуют три взаимоисключающих друг друга варианта расположения прямых в пространстве:

1) Две прямые лежат в одной плоскости и имеют общую точку - пересекающиеся прямые.

2) Две прямые лежат в одной плоскости и не имеют общих точек - параллельные прямые.

3) Две прямые не лежат в одной плоскости.

Две прямые, не лежащие в одной плоскости, называются скрещивающимися.

Две прямые, лежащие в одной плоскости, и не имеющие общих точек называются параллельными.

Теорема. Через каждую точку, не лежащую на данной прямой, проходит прямая, параллельная данной, притом только одна.

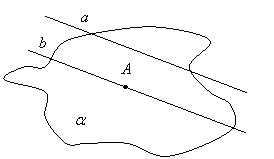Доказательство. Пусть даны прямая a и не лежащая на ней точка А. Согласно теореме, через прямую и не лежащую на ней точку проходит единственная плоскость 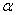. В этой плоскости, как известно из планиметрии, существует прямая b ║ a и проходящая через точку А.

Любая прямая проходящая через точку A и параллельно a, совпадает с прямой b. Итак, в плоскости , по аксиоме параллельности есть только одна прямая, проходящая через точку A параллельно прямой a, - прямая b => в пространстве существует только одна прямая, проходящая через точку A параллельно прямой a.

Лемма. Если плоскость пересекает одну из двух параллельных прямых, то она пересекает и вторую.

Доказательство. Пусть даны прямые a ║ b и плоскость 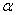, пересекающая a в точке A. Проведём через прямые a и b плоскость 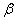. Согласно аксиоме, 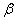пересечёт 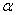по некоторой прямой c. Так как b и c лежат в одной плоскости 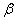, то . Но прямая c также лежит и в плоскости 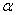, поэтому .

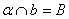Теорема. Две прямые параллельные третьей, параллельны между собой.

Доказательство. Пусть прямые a и b параллельны прямой с. Прямые a и b не имеют общих точек (в противном случае через такую точку проходило бы две прямые, параллельные

прямой с, что невозможно вследствие первой теоремы). Возьмем любую точку 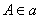. Согласно теореме, через b и A проходит плоскость 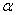. Покажем, что a лежит в плоскости .

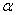Допустим, что это не так, тогда прямая a пересекает 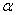в точке А. Согласно лемме, и прямая с должна пересекать 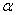, так как с || а. Но поскольку b || с, то, по той же лемме, прямая b тоже должна пересекать 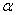, что невозможно, так как по условию b лежит в 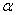. Итак, а и b лежат в плоскости 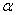и не имеют общих точек, то есть а || b.

Признаки скрещивающихся прямых:

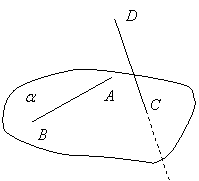1) Если две прямые содержат четыре точки, не лежащие в одной плоскости, то они скрещиваются.

Доказательство. Проведём через точки A, B и C плоскость 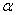. Прямая 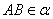, а прямая CD пересекает 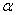, так как 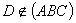по условию. Точка C отлична от точек прямой AB => AB и CD не лежат в одной плоскости => они скрещиваются.

2) Прямая, пересекающая плоскость, скрещивается с каждой прямой, лежащей в этой плоскости и не проходящей через точку пересечения заданной прямой и плоскости.

Доказательство. Пусть прямая 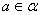, а прямая .

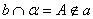По условию, b имеет не более одной общей точки A с плоскостью 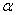. Если взять любые две точки на прямой a, точку A и любую другую точку на b, то прямые a и b будут иметь четыре точки, не лежащие в одной плоскости (так как только три из них принадлежит 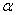). По первому признаку, a и b - скрещивающиеся прямые.

Дата добавления: 2015-04-23