Уравнение полоской и сферической волн

Свойства волн.

Частота, период, длина волны.

Волновое уравнение.

Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением - дифференциальным уравнением в частных производных.

, (4) где (5)-оператор Лапласа, v - фазовая скорость.

Решением уравнения (4) является уравнение любой волны (плоской, сферической и т.д.). В частности, для анализируемой здесь плоской гармонической волны (1), которая не зависит от координат y и z волновое уравнение принимает вид. (6)

Cоответствующей подстановкой можно убедится, что уравнению (6) удовлетворяет уравнение (1).

Длина волны - это расстояние, на которое распространяется волна за один период колебаний.Так как,тоили.

Генерация волн. Волны могут генерироваться различными способами.

Генерация локализованным источником колебаний (излучателем, антенной).

Спонтанная генерация волн в объёме при возникновении гидродинамических неустойчивостей. Такую природу могут иметь, например, волны на воде при достаточно большой скорости ветра, дующего над водной гладью.

Переход волн одного типа в волны другого типа. Например, при распространении электромагнитных волн в кристаллическом твёрдом теле могут генерироваться звуковые волны.

Как правило, волны способны удалиться сколь угодно далеко от генератора колебаний. По этому причине иногда волнами называют «колебание, оторвавшееся от излучателя». Исключение составляют так называемые температурные волны, амплитуда которых экспоненциально спадает при удалении от излучателя.

Волновые процессы представляют собой общий класс явлений.
Несмотря на бесконечное разнообразие физических процессов, вызывающих волны, образование волн происходит по одному общему типу. Возмущение, происшедшее в какой-нибудь точке в известный момент времени, проявляется спустя некоторое время на некотором расстоянии от начальной точки, т. е. передается с определенной скоростью. Рассмотрим самый простой пространственно одномерный случай: распространение возмущения вдоль оси ОХ. Тогда можно изобразить возмущение f как функцию координаты x и времени t, 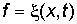. Распространение возмущения со скоростью u вдоль направления ОХ изобразится той же функцией, в аргумент которой t и x входят в комбинаци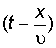и или 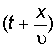в зависимости от направления распространения возмущения вдоль оси ОХ.

В этом случае волновое уравнение (2.5) имеет вид:

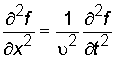, (2.6)

а его общее решение выглядит

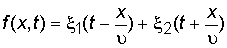. (2.7)

Если в начальный момент времени t = 0 графически изобразить функции x₁(x) и x₂(x), то в последующие моменты времени эти функции будут смещаться вдоль оси ОХ со скоростью u как целое: x₁ – вправо, x₂ – влево.

Рассмотрим гармонические монохроматические волны, т. е. синусоидальные волны с одной циклической частотой w = 2pn.

В этом случае зависимость любой величины f от времени t в общем виде выглядит так:

,

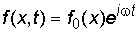где f ₀ – значение рассматриваемой величины в точке с координатой x в начальный момент времени t = 0. Решение волнового уравнения (2.6), удовлетворяющее условию (2.7) и дающее гармоническую зависимость f от t, имеет вид:

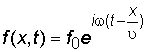. (2.8)

Выражением 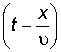в формуле (2.8) определяется фаза волны (ее состояние в данный момент времени в данной точке пространства). В данный момент времени волновой фронт – геометрическое место точек, в которых фаза колебаний имеет одно и то же значение – описывается уравнением x = const. Это плоскость, нормальная к оси OX и перпендикулярная направлению распространения волны. Таким образом, волновой фронт распространяется вправо с фазовой скоростью u. Так как волновой фронт является плоскостью, мы получили плоскую волну. Нам необходимо также выражение для плоской волны, распространяющейся в произвольном направлении, характеризуемом постоянным единичным вектором . Так как уравнение плоскости, перпендикулярной вектору , имеет вид
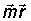= const, уравнение плоской волны можно записать в виде:

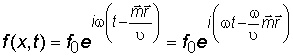. (2.9)

Введем волновой вектор 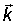, определив его как

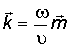. (2.10)

где – единичный вектор в направлении распространения волны (в направлении 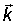). Тогда уравнение плоской волны можно записать в виде:

.

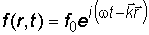Волновой вектор связан с длиной волны l (расстоянием между двумя ближайшими точками волны, находящимися в одинаковой фазе, в данный момент времени), он всегда перпендикулярен фронту волны. Пусть фазы плоской волны (2.9) в точках r и r + l одинаковы. Тогда в любой момент времени должно соблюдаться равенство

.

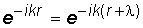Это возможно только, когда 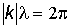, т. е. .

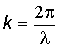Рассмотрим монохроматические плоские волны. В однородной изотропной непроводящей среде векторы напряженностей электрического и магнитного 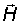полей изменяются в соответствии с волновыми уравнениями (2.3) и (2.4) при соблюдении (2.10), когда 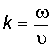. Тогда уравнениям (2.3) и (2.4) удовлетворяют выражения:

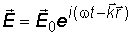; (2.11)

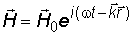. (2.12)

Уравнения (2.11) и (2.12) являются уравнениями плоской электромагнитной волны, записанными в комплексной форме. Вектор 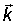определяет направление распространения волны. Векторы и 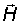колеблются в плоскости, перпендикулярной направлению 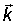. Так как направление колебаний перпендикулярно направлению распространения волны, то электромагнитная волна в данных условиях является поперечно-поляризованной. Уравнения плоской электромагнитной волны можно записать также в следующем виде:

;

.

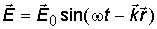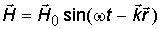Результаты, полученные для монохроматических плоских волн, будут справедливы для любых плоских волн.

Если источник возмущения мал (точка) и скорость распространения возмущения во все стороны одинакова (изотропная среда), то фронт волны должен иметь вид сферической поверхности с центром в источнике.
В таком случае волна называется сферической. Уравнение такой монохроматической сферической волны имеет вид:

,

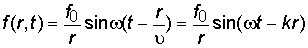где 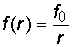– амплитуда волны, f ₀ – амплитуда на единичном расстоянии r от источника. Выражение это показывает, что амплитуда сферической волны уменьшается пропорционально расстоянию от источника.

Уравнения сферической монохроматической электромагнитной волны можно записать в следующем виде:

,

.

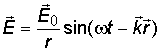В комплексной форме эти уравнения принимают вид:

,

.

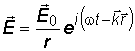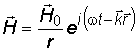Сферическая волна соответствует источнику точечного размера, т. е. представляет абстракцию. Однако даже при источнике конечного размера фронт волны на достаточно большом расстоянии r будет сферической поверхностью с достаточным приближением.

В практической оптике для многих задач можно считать фронт сферическим, если расстояние r превосходит линейные размеры источника в десять раз или более.

Дата добавления: 2015-04-23