
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вывод уравнения плоской бегущей волны
|
|
|
|
Длина волны и волновое число
Длиной волны  – называют расстояние между ближайшими точками, колеблющимися в одинаковой фазе.
– называют расстояние между ближайшими точками, колеблющимися в одинаковой фазе.
Формулы длины волны легко получить из аналогии по формуле пути:
 (1)
(1)
 (2)
(2)
 Если период равен
Если период равен  , (3)
, (3)
то  (4)
(4)
Если из (2) выразить период и приравнять его к (3), получим:
 получим
получим 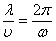 (5)
(5)
Или  (6)
(6)
Физический смысл отношения  заключается в том, что оно показывает сколько длин волн умещается в
заключается в том, что оно показывает сколько длин волн умещается в  единицах длины. Отношение
единицах длины. Отношение  обозначается
обозначается  и называется волновым числом, т.е.
и называется волновым числом, т.е.

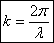
 (7)
(7)

Например:
Бегущие волны – волны, которые переносят в пространстве энергию.
Плоские волны – волны, волновые поверхности которых – есть совокупность параллельных плоскостей, перпендикулярных направлению распространения волны.
Лучи в этом случае – параллельные прямые, совпадающие с направлением скорости распространения волны.
Пусть плоская бегущая волна распространяется вдоль оси X, т.е. вдоль одного направления из точки А в точку В как показано на рисунке:
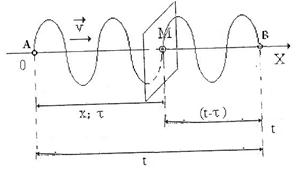 Пусть источник колебаний в начальный момент времени
Пусть источник колебаний в начальный момент времени 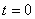 находится в точке О.
находится в точке О.
Запишем уравнение колебания:
 (8)
(8)
Рассмотрим распространение волны от точки М до точки В. Из рисунка видно, что время  , затраченное на этот путь равно
, затраченное на этот путь равно  , где
, где 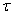 - это время, за которое волна распространилась от источника колебаний до точки М.
- это время, за которое волна распространилась от источника колебаний до точки М.
Перейдем от уравнения колебаний к уравнению плоской бегущей волны:
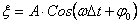 (9)
(9)
 (10)
(10)
Т.к. за время 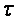 волна распространилась на расстояние
волна распространилась на расстояние  , тогда
, тогда
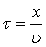 (11)
(11)
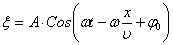 (12)
(12)
 (13)
(13)
Будем считать начальную фазу  .
.
Тогда согласно уравнению (6), получаем:  (14)
(14)
Если в уравнении (14)  , а
, а  , то получим четвертый вид уравнения плоской бегущей волны (при
, то получим четвертый вид уравнения плоской бегущей волны (при  ):
):

| - первый вид уравнения плоской бегущей волны |
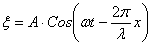
| - второй вид уравнения плоской бегущей волны |
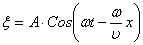
| - третий вид уравнения плоской бегущей волны |
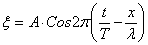
| - четвертый вид уравнения плоской бегущей волны |
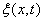 - смещение точек среды с координатой x в момент времени t.
- смещение точек среды с координатой x в момент времени t.
|
|
|
|
|
Дата добавления: 2015-04-23; Просмотров: 3290; Нарушение авторских прав?; Мы поможем в написании вашей работы!