Оценка значимости коэффициентов регрессии

Опишите схему проверки гипотез о величине коэффициентов регрессии.

Для расчёта значимости коэффициентов регрессии используется критерий Стьюдента. Вычисляются 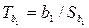, 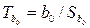и сравниваются с t_крит. Результатом сравнения является вывод о значимости коэффициентов b ₀ и b ₁.

Найдем S, , .

= = 0,066142003; Отсюда S =0,257180876.

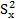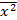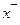= -()² = 6,8536

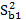= /n* 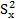= 0,001206; Отсюда 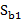= 0,034732.

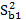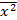= * = 0,131022; Отсюда 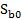= 0,361969.

Проверим значимость обоих коэффициентов:

Значимость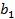

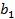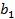: = 0

: ≠ 0

T_b1 = 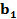/ = 0,49753/0,034732= 14,32457

Данное значение не входит в интервал ± , следовательно, принимаем гипотезу : 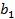≠ 0, это говорит нам о том, что коэффициент значим.

Значимость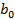

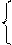
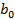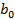: = 0

: ≠ 0

T_b0 = / = 1,06870/0,361969=2,952466

Данное значение тоже не входит в интервал ± , следовательно, принимаем гипотезу и 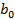является значимым.

6)В чем суть статистической значимости коэффициентов регрессии?

Проверка статистической значимости коэффициентов линейной регрессии заключается в проверке гипотезы значимости или незначимости отличия оценок некоторых регрессионных коэффициентов от нуля. Если в результате проверки оказывается, что отличие оценок каких-то регрессионных коэффициентов от нуля не влияет на качество модели, то соответствующие предикторные переменные можно исключить из регрессионной модели.Если верна гипотеза Но, то коэффициент является не значимым для уравнения регрессии, если верна гипотеза Н1, то коэффициент значим.

Дата добавления: 2015-04-23