Причин существования случайной составляющей несколько

1. Не включение объясняющих переменных.

2. Агрегирование переменных.

3. Выборочный характер исходных данных.

4. Неправильная функциональная спецификация.

5. Возможные ошибки измерения.

Если случайный член ε нормально распределен, то так же будут распределены и коэффициенты регрессии. Это условие необходимо для проводения проверки гипотез и определять доверительные интервалы для a и b, используя результаты построения регрессии.
12) Перечислите предпосылки классической модели линейной регрессии.
Предпосылками построения классической линейной регрессионной модели являются четыре условия, известные как условия Гаусса-Маркова.

· В уравнении линейной модели Y=a+b*X+ε слагаемое ε - случайная величина, которая выражает случайный характер результирующей переменной Y.

· Математическое ожидание случайного члена в любом наблюдении равно нулю, а дисперсия постоянна.

· Случайные члены для любых двух разных наблюдений независимы (некоррелированы).

· Распределение случайного члена является нормальными

13) Что такое «несмещенная оценка коэффициентов уравнения регрессии»?
Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным исследованиям.

14)Что такое «эффективная оценка коэффициента уравнения регрессии»?
Оценки считаются эффективными, если они характеризуются наименьшей дисперсией. В практических исследованиях это означает возможность перехода от точечного оценивания к интервальному.
15)Что такое «состоятельная оценка коэффициента уравнения регрессии»?
Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки. Большой практический интерес представляют те результаты регрессии, для которых доверительный интервал ожидаемого значения параметра регрессии biимеет предел значений вероятности, равный единице. Иными словами, вероятность получения оценки на заданном расстоянии от истинного значения параметра близка к единице.

16)В чем суть метода МНК для построения множественного линейного уравнения регрессии?
Классический подход к оцениванию параметров линейной модели множественной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака от расчетных 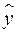минимальна:

.
17)Приведите формулы расчета коэффициентов эмпирического линейного уравнения по МНК в матричной форме.

Для определения оценок b ₀, b ₁, b ₂, …, b _m воспользуемся матричным МНК. Представим данные наблюдений и коэффициенты в матричном виде:

, , , .

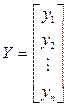Результатом МНК будет формула вычисления коэффициентов регрессии: B = (X^T X)^-1 X^T Y.

18)Как проверить статистическую значимость регрессионного уравнения?
Значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера:

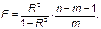
Частный F-критерий оценивает статистическую значимость присутствия каждого факторов в уравнении. В общем виде для фактора частный F-критерий определится как

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – показателя детерминации.

Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком или, иначе, оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:

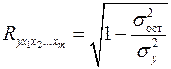, (2.12)

где – общая дисперсия результативного признака; 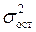– остаточная дисперсия.

Границы изменения индекса множественной корреляции от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции:

.

19)Как проверить статистическую значимость коэффициента детерминации?

Статистическую значимость коэффициента детерминации можно с помощью распределения Фишера. Применяется F-статистика.
20)Чем скорректированный коэффициент детерминации отличается от обычного?

Классический коэффициент множественной детерминации не всегда способен определить влияние на качество модели регрессии дополнительной факторной переменной. Поэтому наряду с обычным коэффициентом рассчитывают также и скорректированный (adjusted) коэффициент множественной детерминации, в котором учитывается количество факторных переменных, включённых в модель регрессии.
скорректированный коэффициент детерминации:

.

21)Как осуществляется анализ статистической значимости коэффициента детерминации?
По величине R ² можно только предполагать насколько значимо или не значимо уравнение регрессии. Даже при небольшой величине R ² (< 0,5) не всегда следует отказываться от уравнения регрессии. Для этого необходимо проверить статистическую значимость самого коэффициента детерминации. Для чего проверяются гипотезы

Н ₀: R ² = 0,

Н ₁: R ² > 0.

Для проверки используется распределение Фишера. Вычисляется F – статистика: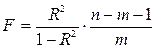

. При заданном уровне значимости 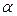по таблице критических точек Фишера находится f_кр, и если F > f_кр, то R ² статистически значим.

22)Как используется F- статистика в регрессионном анализе?
F-статистика используется для проверки значимости коэффициента детерминации.

23)В чем суть статистики Дарбина-Уотсона и как она связана с коэффициентом корреляции между соседними отклонениями?
Критерий Дарбина — Уотсона (или DW-критерий) — статистический критерий, используемый для тестирования автокорреляции первого порядка элементов исследуемой последовательности. Наиболее часто применяется при анализе временных рядов и остатков регрессионных моделей. Статистика Дарбина – Уотсона, устанавливает, в частности, наличие или отсутствие статистической зависимости между ошибками . Так как истинные значения неизвестны, то проверка осуществляется в отношении оценок ошибок е_i. При этом проверяется некоррелированность соседних значений е_i.

Статистика Дарбина – Уотсона DW рассчитывается по формуле:

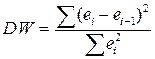
24)Как анализируется статистическая значимость статистики Дарбина-Уотсона?

Статистика Дарбина – Уотсона DW рассчитывается по формуле:

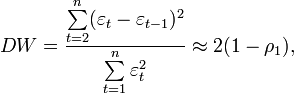
где 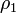— коэффициент автокорреляции первого порядка.

В случае отсутствия автокорреляции , при положительной автокорреляции 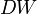стремится к нулю, а при отрицательной — к 4:

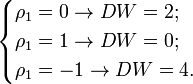
На практике применение критерия Дарбина — Уотсона основано на сравнении величины 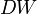с теоретическими значениями 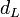и для заданных числа наблюдений 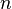, числа независимых переменных модели 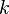и уровня значимости .

1. Если 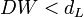, то гипотеза о независимости случайных отклонений отвергается (следовательно присутствует положительная автокорреляция);
2. Если 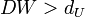, то гипотеза не отвергается;
3. Если , то нет достаточных оснований для принятия решений.

Когда расчетное значение 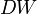превышает 2, то с 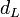и сравнивается не сам коэффициент 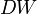, а выражение 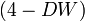^[2].
25)Приведите примеры нелинейных моделей, используемых в эконометрике.
Нелинейные модели, являющиеся линейными относительно параметров, сводятся к линейным простой заменой переменных. Нелинейные модели, которые сводятся к линейным после некоторых преобразований с последующей заменой переменных, называются внутренне линейными. Нелинейные модели, которые нельзя преобразовать к линейной форме, называются внутренне нелинейными. С помощью t- и F-статистики исследуют линеаризованную модель.

Примеры нелинейных моделей: Степенные модели, Гиперболические модели, Экспоненциальные, Логарифмические, показательные.

26)Какие из известных вам типов нелинейных моделей поддаются непосредственной линеаризации?
Непосредственной линеаризации поддаются модели степенного, гиперболического и экспоненциального, показательного и логарифмического вида.
27)Как линеаризуются модели гиперболического вида?
1. Положим, что переменные х и у и регрессионные остатки связаны между собой зависимостью вида

(49)

Кривая регрессии является гипербола.

С помощью преобразования объясняющей переменной эта зависимость приводится к линейной:

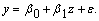
Соответственно при вычислении МНК-оценок параметров 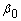и 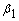второй столбец должен быть сформирован из чисел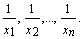

2. Положим, что переменные х и у и регрессионные остатки связаны между собой зависимостью вида

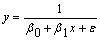
Введя новую переменную получим линейную модель

При вычислении МНК-оценок необходимо помнить, что в качестве вектора наблюденных значений зависимой переменной есть вектор

3. Если модель сводится к уравнению

то введением новых переменных и уравнение сводится к линейному

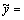
28) Как линеаризуются модели эскпоненциального вида?

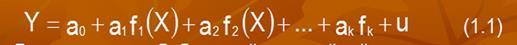
29) Как линеаризуются модели степенного вида?

30) Как линеаризуются модели логарифмического вида?

31)Каковы признаки качественной регрессионной модели?

1. Скупость (простота). Из двух моделей, приблизительно одинаково отражающих реальность, предпочтение отдается содержащей меньшее число объясняющих переменных.
2. Единственность. Для любого набора статистических данных определяемые коэффициенты должны вычисляться однозначно.
3. Максимальное соответствие. Уравнение тем лучше, чем большую часть разброса зависимой переменной оно может объяснить. Поэтому стремятся построить уравнение с максимально возможным скорректированным коэффициентом детерминации R².
4. Согласованность с теорией. Никакое уравнение не может быть признано качественным, если оно не соответствует известным теоретическим предпосылкам. Вообще говоря, теория тоже может оказаться ошибочной.
5. Прогнозные качества. Модель может быть признана качественной, если полученные на ее основе прогнозы подтверждаются реальностью.
6. Другим критерием прогнозных качеств оцененной модели регрессии может служить следующее отношение: V = S/yср, где S — стандартная ошибка регрессии, y — среднее значение зависимой переменной уравнения регрессии. Если величина V мала (а она определяет относительную ошибку прогноза в процентах) и отсутствует автокорреляция остатков (определяемая по величине статистики DW Дарбина-Уотсона), то прогнозные качества модели высоки.

Дата добавления: 2015-04-23