Ошибки спецификации

Назовите основные виды ошибок спецификации.

Рассмотрим виды ошибок спецификации. Одним из базовых предположений построения качественной модели является правильная (хорошая) спецификация уравнения регрессии. Правильная спецификация уравнения регрессии означает, что оно в целом верно, отражает соотношение между экономическими показателями, участвующими в модели. Это является необходимой предпосылкой дальнейшего качественного оценивания.

Неправильный выбор функциональной формы или набора объясняющих переменных называется ошибками спецификации. Рассмотрим основные типы ошибок спецификации.

1. Отбрасывание значимой переменной. Последствия данной ошибки достаточно серьезны. Оценки, полученные с помощью МНК, являются смещенными и несостоятельными даже при бесконечно большом числе испытаний. Следовательно, возможные интервальные оценки и результаты проверки соответствующих гипотез будут ненадежными.
2. Добавление незначимой переменной. В некоторых случаях в уравнения регрессии включают слишком много объясняющих переменных, причем не всегда обоснованно. Последствия данной ошибки будут не столь серьезными, как в предыдущем случае. Оценки коэффициентов модели остаются, как правило, несмещенными и состоятельными. Однако их точность уменьшается, увеличивая при этом стандартные ошибки, т. е. оценки становятся неэффективными, что отразится на их устойчивости.
3. Выбор неправильной функциональной формы. Последствия такой ошибки будут весьма серьезными. Обычно ошибка приводит либо к получению смещенных оценок, либо к ухудшению статистических свойств оценок коэффициентов регрессии и других показателей качества уравнения. В первую очередь это связано с нарушением условий Гаусса-Маркова для отклонений. Прогнозные качества модели в этом случае очень низки.

33)Как можно обнаружить ошибки спецификации?

При построении уравнений регрессии, особенно на начальных этапах, ошибки спецификации весьма нередки. Они допускаются обычно из-за поверхностных знаний об исследуемых экономических процессах либо из-за недостаточно глубоко проработанной теории, или из-за погрешностей сбора и обработки статистических данных при построении эмпирического уравнения регрессии. Важно уметь обнаружить и исправить эти ошибки. Сложность процедуры определяется типом ошибки и нашими знаниями об исследуемом объекте.

Если в уравнении регрессии имеется одна несущественная переменная, то она обнаружит себя по низкой t-статистике. В дальнейшем эту переменную исключают из рассмотрения.

Если в уравнении несколько статистически незначимых объясняющих переменных, то следует построить другое уравнение регрессии без этих незначимых переменных. Затем с помощью F-статистики

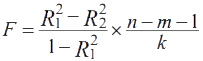
сравниваются коэффициенты детерминации для первоначального и дополнительного уравнений регрессий. Здесь n — число наблюдений, m — число объясняющих переменных в первоначальном уравнении, k — число отбрасываемых из первоначального уравнения объясняющих переменных.

34)Можно ли обнаружить ошибки спецификации с помощью исследования остаточного члена?
Да, для более детального анализа адекватности модели может быть предложено исследование остаточного члена модели.

35)В чем суть теста Рамсея?

RESET-тест Рамсея (сокр. от англ. Regression Equation Specification Error Test) - применяемая в эконометрике процедура тестирования функциональной формы (спецификации) модели.

Тест основан на вспомогательной регрессии зависимой переменной на факторы исходной модели плюс различные степени оцененных по исходной модели значений зависимой переменной:

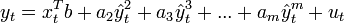
Далее необходимо проверить гипотезу: 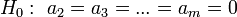. Данную гипотезу проверяют с помощью F-теста, LR-теста или теста Вальда.

Если значение статистики больше критического, то нулевая гипотеза отвергается и спецификация модели признается неверной. В противном случае функциональная форма модели является приемлемой.

36) Что такое гомоскедастичность и гетероскедастичность?

Предположение о том, что ошибки 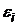наблюдений имеют одинаковые дисперсии, называется гомоскедастичностью. Если же ошибки 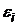наблюдений имеют разные дисперсии, то говорят о гетероскедастичности наблюдений.

37)Приведите пример взаимоотношений в экономике, описываемых моделью с гетероскедастичными остатками.

38)Каким образом осуществляется проверка экономической модели на гетероскедастичность?

Чтобы определить, присутствует ли гетероскедастичность на самом деле, применяют различные тесты.

Все тесты основаны на предположении о наличии связи между дисперсиями остатков моделей и объясняющими переменными или расчетными значениями зависимой переменной в случае гетероскедастичности.

Эта связь обнаруживается с помощью коэффициента ранговой корреляции в тесте ранговой корреляции Спирмена, либо предполагается пропорциональность стандартных отклонений 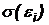и зависимой переменной Y в тесте Голдфелда-Квандта, либо строятся различные линейные и нелинейные регрессии 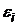, 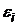2, 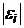на объясняющие переменные или степени зависимой переменной Y и проверяется значимость полученных коэффициентов регрессии в тесте Уайта.

39)Почему нельзя применять классический МНК в случае гетероскедастичности?

Наличие гетероскедастичности случайных ошибок приводит к неэффективности оценок, полученных с помощью метода наименьших квадратов. Кроме того, в этом случае оказывается смещённой и несостоятельной классическая оценка ковариационной матрицы МНК-оценок параметров. Следовательно статистические выводы о качестве полученных оценок могут быть неадекватными. В связи с этим тестирование моделей на гетероскедастичность является одной из необходимых процедур при построении регрессионных моделей.
40)Какие преобразования исходных данных нужно провести в случае обраружения гетероскедастичности?

1-й общий подход к решению данной проблемы состоит в преобразовании исходных данных таким образом, чтобы для преобразованных данных модель уже обладала свойством гомоскедастичности. Применяют чаще всего два вида преобразований а) логарифмирование данных; б) переход к безразмерным величинам путем деления на некоторые известные величины, той же размерности, что и исходные данные. Возможна также стандартизация исходных данных.

Второй подход состоит в применении взвешенного и обобщенного метода наименьших квадратов.

Вычитая из данных X(ti) выровненные значения 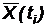, получаем остатки, случайную составляющую тренда

e(t) =X(t) - .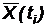

41)В чем суть метода взвешанных наименьших квадратов (ВМНК)?
Из-за неэффективности оценок, полученных методом наименьших квадратов (МНК) при наличии гетероскедастичности, взвешенный метод наименьших квадратов (ВМНК). В этом методе вклад данных наблюдений, имеющих большую дисперсию, уменьшается.

42)Как вы понимаете термин «автокорреляция остатков»?
В эконометрических исследованиях часто возникают и такие ситуации, когда дисперсия остатков постоянная, но наблюдается их ковариация. Это явление называют автокорреляцией остатков. Автокорреляция остатков чаще всего наблюдается тогда, когда эконометрическая модель строится на основе временных рядов. Если существует корреляция между последовательными значениями некоторой независимой переменной, то будет наблюдаться и корреляция последовательных значений остатков.

43)Приведите пример взаимоотношений в экономике, описываемых моделью с автокорреляционными остатками.
Проиллюстрируем проблему автокорреляции остатков на примере эконометрической модели с двумя переменными. Пусть

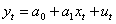(1)

где мы предполагаем, что остатки u_t, удовлетворяют схему авторегресии первого порядка, то есть зависят только от остатков предыдущего периода:

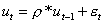(2)

для которой |ρ| < 1, а ε_t имеют такие свойства:

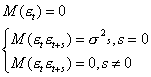
Величина ρ характеризует уровень взаимосвязи каждого следующего значения с предыдущим то есть ковариацию остатков.

Спецификация модели (1) имеет индекс t, что свидетельствует о ее динамическом характере, то есть и — период времени, для которого строится такая модель динамических (временных) рядов исходных данных.

Рассмотрим остатки модели u_t, учитывая (2):

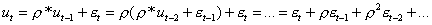
Отсюда

.

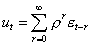Поскольку: 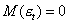, то .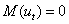

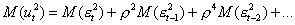
Учитывая, что последовательные значения 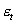, независимы, запишем

.

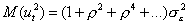Тогда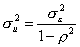

.

Ковариация последовательных значений остатков запишется в виде

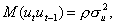
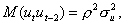
и в общем случае

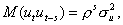
то есть для модели (1) не удовлетворяется гипотеза о независимости последовательных значений остатков.

Выражение можно записать так:

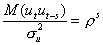
Это означает, что при наличии автокорреляции остатков второе необходимое условие подается в виде:

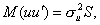
где S - матрица коэффициентов автокорреляции s-го порядка для ряда u_t ,, или

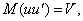
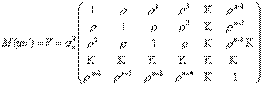. (7)

Сравнив матрицу, которую имеем в данном случае, с матрицей при наличии гетероскедастичности, увидим, что они существенным образом отличаются одна от другой. Это связано с тем, как понимается второе условие для применения метода МНК при явлении гетероскедастичности и автокорреляции.

44)Каковы последствия применения классического МНК к модели с автокоррелированными остатками?

Полученные оценки будут неэффективны. Т.к. они не будут иметь минимальную дисперсию. Это приводит к увеличению стандартных ошибок, снижению фактических значений t-критерия и широким доверительным интервалам для коэффициента регрессии. На основе таких результатов можно сделать ошибочный вывод о незначимом влиянии исследуемого фактора на результат, в то время как на самом деле его влияние статистически значимо.

Отметим, что при соблюдении прочих предпосылок МНК автокорреляция остатков не влияет на свойства состоятельности и несмещенности оценок параметров уравнения регрессии обычным МНК, за исключением моделей авторегрессии.

45)Каким образом осуществляется проверка эконометрической модели на автокорреляцию остатков?

Первый метод — это построение графика зависимостей остатков от времени и визуальное определение наличия автокорреляции остатков.

Второй метод - расчет критерия Дарбина - Уотсона

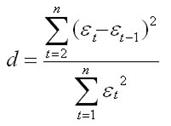
Т.е. Критерий Дарбина - Уотсона определяется как отношение суммы квадратов разностей последовательных значений остатков к сумме квадратов остатков. Практически во всех задачах по эконометрике значение критерия Дарбина — Уотсона указывается наряду с коэффициентом корреляции, значениями критериев Фишера и Стьюдента

Коэффициент автокорреляции первого порядка определяется по формуле

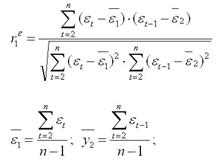
Соотношение между критерием Дарбина — Уотсона и коэффициентом автокорреляции остатков (r1) первого порядка определяется зависимостью

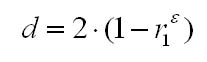
Т.е. если в остатках существует полная положительная автокорреляция r1 = 1, а d = 0, Если в остатках полная отрицательная автокорреляция, то r1 = — 1, d = 4. Если автокорреляция остатков отсутствует, то r1 = 0, d = 2. Следовательно,

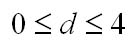
46)Опишите схему использования статистики Дарбина-Уотсона.

По таблицам критических точек Дарбина – Уотсона, входными параметрами которых являются: n – число наблюдений; m – количество объясняющих переменных; 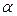- уровень значимости, определяются два числа: d ₁ – нижняя граница; d_u – верхняя граница.

Выводы осуществляются по следующей схеме.

Если DW < d ₁, то это свидетельствует о положительной автокорреляции остатков.

Если DW > 4 - d ₁, то это свидетельствует об отрицательной автокорреляции остатков.

При d_u < DW < 4 – d_u принимается гипотеза об отсутствии автокорреляции остатков.

Если d ₁ < DW < d_u или 4 – d_u < DW < 4 – d ₁, то остается неопределенность по вопросу наличия или отсутствия автокорреляции остатков.

47)Какие преобразования исходных данных нужно провести в случае обнаружения автокорреляции остатков?

48)Что такое мультиколлинеарность?

Мультиколлинеарность - тесная корреляционная взаимосвязь между отбираемыми для анализа факторами, совместно воздействующими на общий результат, которая затрудняет оценивание регрессионных параметров.

49)По каким проявлениям можно судить о наличии мультиколлинеарности в оцененной модели?

Если регрессоры в модели связаны строгой функциональной зависимостью, то имеет место полная (совершенная) мультиколлинеарность. Данный вид мультиколлинеарности может возникнуть, например, в задаче линейной регрессии, решаемой методом наименьших квадратов, если определитель матрицы 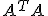будет равен нулю. Полная мультиколлинеарность не позволяет однозначно оценить параметры исходной модели и разделить вклады регрессоров в выходную переменную по результатм наблюдений.

В задачах с реальными данными случай полной мультиколлинеарности встречается крайне редко. Вместо этого в прикладной области часто приходится иметь дело с частичной мультиколлинеарностью, которая характеризуется коэффициентами парной корреляции между регрессорами. В случае частичной мультиколлинеарности матрица 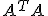будет иметь полный ранг, но ее определитель будет близок к нулю. В этом случае формально можно получить оценки параметров модели и их точностные показатели, но все они будут неустойчивыми.

50) Каковы негативные последствия мультиколлинеарности?

Характеризуя в целом последствия мультиколлинеарности, отметим, что при ее наличии снижается точность оценок регрессионных коэффициентов (стандартные ошибки коэффициентов получаются слишком большими); становится невозможной оценка статистической значимости коэффициентов регрессии с помощью t -критерия, отсюда вероятно некорректное введение в анализ тех или иных переменных; резко возрастает чувствительность коэффициентов регрессии к особенностям исходных данных
51)Перечислите основные методы устранения мультиколлинеарности.

К основным способам устранения мультиколлинеарности в модели множественной регрессии относятся:

1) один из наиболее простых способов устранения мультиколлинеарности состоит в получении дополнительных данных. Однако на практике в некоторых случаях реализация данного метода может быть весьма затруднительна;

2) способ преобразования переменных, например, вместо значений всех переменных, участвующих в модели (и результативной в том числе) можно взять их логарифмы:

lny=β0+β1lnx1+β2lnx2+ε.

52)Перечислите основные элементы временного ряда.
Временной ряд – ряд изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке.

2 основных элемента: время t, уровень ряда y

53) Что такое автокорреляция уровней временного ряда и как её можно оценить количественно?

Автокорреляция уровней ряда – это корреляционная зависимость между последовательными уровнями временного ряда:

,

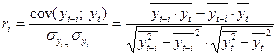где , .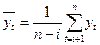

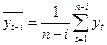Дата добавления: 2015-04-23