
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Законы Кеплера и обобщение Ньютона (закон всемирного тяготения). Сила тяжести. Поле тяготения. Космические скорости
|
|
|
|
1) Все планеты движутся по эллиптическим орбитам, причем Солнце находится в одном из фокусов орбиты.
2) Отрезок, соединяющий Солнце с планетой, описывает равные площади за равные промежутки времени.
3) Квадраты периодов обращения нескольких планет вокруг Солнца относятся, как кубы больших полуосей эллипсов. 
1) Мы показали, что замкнутые орбиты являются эллипсами.
2) Второй закон Кеплера представляет собой закон сохранения момента импульса. 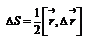 - вектор площади треугольника.
- вектор площади треугольника.  - секторальная площадь.
- секторальная площадь. 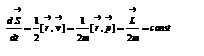
 3) Для эллипсов вывод более громоздкий, но для круговых орбит просто:
3) Для эллипсов вывод более громоздкий, но для круговых орбит просто:




Кеплеровские законы были уточнены и объяснены на основе закона всемирного тяготения Исааком Ньютоном. Закон же всемирного тяготения гласит:
Сила F взаимного притяжения между материальными точками массами m1 и m2, находящиеся на расстоянии r друг от друга, равна: F=Gm1m2/r^2, где G - гравитационная постоянная. Закон открыт Ньютоном также в XVII веке (понятно, что на основе законов Кеплера).
Таким образом в формулировке Ньютона законы Кеплера звучат так:
- первый закон: под дествием силы тяготения одно небесное тело может двигаться по отношению к другому по окружности, эллипсу, параболе и гиперболе. Надо сказать, что он справедлив для всех тел, между которыми действует взаимное притяжение.
- формулирование второго закона Кеплера не дана, так как в этом не было необходимости.
- третий закон Кеплера сформулирован Ньютоном так: квадраты сидерических периодов планет, умноженные на сумму масс Солнца и планеты, относятся как кубы больших полуосей орбит планет.
СИЛА ТЯЖЕСТИ Частным, но крайне важным для нас видом силы всемирного тяготения является сила притяжения тел к Земле. Эту силу называют силой тяжести. Согласно закону всемирного тяготения, она выражается формулой 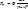
где  – масса тела, М – масса Земли, R – радиус Земли, h – высота тела над поверхностью Земли. Сила тяжести направлена вертикально вниз, к центру Земли.
– масса тела, М – масса Земли, R – радиус Земли, h – высота тела над поверхностью Земли. Сила тяжести направлена вертикально вниз, к центру Земли.
ГРАВИТАЦИОННОЕ ПОЛЕ, пространство вокруг предмета, чья масса способна притягивать другой предмет. Сила этого притяжения, разделенная на массу второго предмета, и есть сила гравитационного поля. Предмет с большой массой, такой как Земля, имеет мощное гравитационное поле, и оказываемое им воздействие называется силой гравитации (или тяготения). Слабая гравитационная сила существует даже между очень маленькими частицами.
Элементарная работа перемещения тела массой m в поле тяготения небесного тела массой М равна  где r — расстояние между центрами масс обоих тел, G — гравитационная постоянная. Изменение потенциальной энергии тела, когда его расстояние до центра тяготения меняется от r 1 до r 2, равно работе, совершаемой над телом при таком перемещении:
где r — расстояние между центрами масс обоих тел, G — гравитационная постоянная. Изменение потенциальной энергии тела, когда его расстояние до центра тяготения меняется от r 1 до r 2, равно работе, совершаемой над телом при таком перемещении: 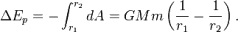 Подсчитаем минимальную энергию, требующуюся для выведения космического корабля на круговую орбиту радиусом r с поверхности планеты радиусом r 0. В этом случае нам необходимо не только изменить потенциальную энергию корабля в поле тяготения, но и сообщить ему некоторую кинетическую энергию для обращения по круговой орбите. Скорость обращения находится из условия равенства ускорения свободного падения и центростремительного ускорения:
Подсчитаем минимальную энергию, требующуюся для выведения космического корабля на круговую орбиту радиусом r с поверхности планеты радиусом r 0. В этом случае нам необходимо не только изменить потенциальную энергию корабля в поле тяготения, но и сообщить ему некоторую кинетическую энергию для обращения по круговой орбите. Скорость обращения находится из условия равенства ускорения свободного падения и центростремительного ускорения: 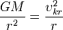 и составляет
и составляет 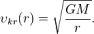 Тогда минимальная кинетическая энергия, которую должны сообщить кораблю двигатели при взлете, равна
Тогда минимальная кинетическая энергия, которую должны сообщить кораблю двигатели при взлете, равна 
откуда находим взлетную скорость, позволяющую вывести корабль на круговую орбиту радиусом r: 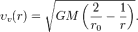 Возьмем вначале радиус орбиты r = r 0. Тогда
Возьмем вначале радиус орбиты r = r 0. Тогда 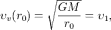 где υ 1 — первая космическая скорость для рассматриваемой планеты. Для Земли, которая естественно интересует нас прежде всего, υ 1z = 7,9 км/с. Пусть теперь
где υ 1 — первая космическая скорость для рассматриваемой планеты. Для Земли, которая естественно интересует нас прежде всего, υ 1z = 7,9 км/с. Пусть теперь  , т. е. корабль, стартуя с поверхности планеты, имеет такую скорость, что способен преодолеть узы тяготения планеты и удалиться от нее на произвольно большое расстояние. При этом корабль будет двигаться по параболической траектории. По этой причине такая скорость носит название параболической относительно данной планеты, или второй космической. Она равна
, т. е. корабль, стартуя с поверхности планеты, имеет такую скорость, что способен преодолеть узы тяготения планеты и удалиться от нее на произвольно большое расстояние. При этом корабль будет двигаться по параболической траектории. По этой причине такая скорость носит название параболической относительно данной планеты, или второй космической. Она равна

Для Земли υ 2z = 11,2 км/с.
Все эти рассуждения справедливы для изолированной планеты. Однако, если планета входит в планетную систему, имеющую центральное светило — Солнце, то, освободившись от тяготения планеты, корабль отнюдь не избавится от притяжения Солнца. Теперь он станет обращаться по замкнутой траектории вокруг Солнца.
Чтобы разорвать путы солнечного притяжения, мы должны сообщить кораблю параболическую скорость относительно Солнца:
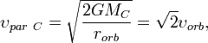 где M C — масса Солнца, r orb — радиус орбиты планеты, которую мы для простоты считаем круговой, υ orb — скорость орбитального движения планеты.
где M C — масса Солнца, r orb — радиус орбиты планеты, которую мы для простоты считаем круговой, υ orb — скорость орбитального движения планеты.
Для Земли υ orb = 29,8 км/с и υ par C = 42,1 км/с.
Означает ли это, что мы обязаны разогнать корабль до скорости 42,1 км/с для того, чтобы он ушел произвольно далеко от Солнца? Конечно, нет, ведь мы можем использовать грандиозную катапульту, которой снабдила нас природа,— Землю, несущуюся по своей орбите со скоростью υ orb. Легко понять, что для Земли скорость, позволяющая, хотя бы в принципе, долететь до любого космического объекта, расположенного в плоскости орбиты Земли за пределами Солнечной системы,— третья космическая скорость — равна 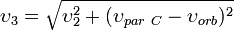 = 16,7 км/с.
= 16,7 км/с.
Итак, сообщив кораблю скорость υ 3 у поверхности Земли, мы можем послать его к любой звезде, лежащей в плоскости обращения Земли. К любой, кроме ближайшей — Солнца!
|
|
|
|
|
Дата добавления: 2015-04-23; Просмотров: 3394; Нарушение авторских прав?; Мы поможем в написании вашей работы!