Истечение жидкости из отверстия

Понятие потока жидкости (газа) и уравнение непрерывности. Вывод уравнения Бернулли. Теорема Торричелли. Течение в горизонтальной трубе.

Состояние движения жидкости можно определить, указав для каждой точки пространства вектор скорости 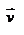, как функцию времени 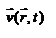. Стационарное течение – это установившееся движение жидкости, при котором вектор скорости в каждой точке пространства остаётся постоянным, т.е. 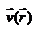. Линии тока - это линии, проведённые в движущейся жидкости так, что касательные к ним в каждой точке совпадают по направлению с вектором скорости 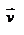. Густота линий тока пропорциональна величине скорости в данном месте. Трубка тока – это часть жидкости, ограниченная линиями тока.Частицы жидкости при своём движении не пересекают стенок трубки тока. 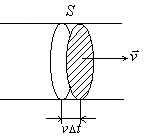Возьмем несжимаемую жидкость и рассмотрим в ней трубку тока. Объём жидкости, прошедшей через поперечное сечение S за время D t, равен Sv D t. Тогда Q = Sv - поток жидкости, т.е. объём жидкости, прошедшей через поперечное сечение S за единицу времени. 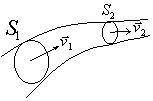Если жидкость несжимаема, то объем жидкости между сечениями S ₁ и S ₂ будет оставаться неизменным, и тогда S ₁ v ₁ = S ₂ v ₂. Это справедливо для любой пары S ₁ и S ₂, и мы получаем Sv = const – теорема о неразрывности струи: Для несжимаемой жидкости величина потока жидкости Sv в любом сечении одной и той же трубки тока должна быть одинаковой.

Стационарное движение идеальной жидкости. Уравнение Бернулли. Идеальная жидкость – жидкость, в которой внутреннее трение (вязкость) полностью отсутствует. 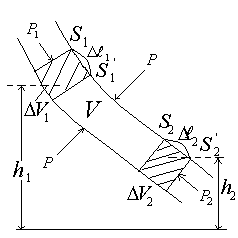Рассмотрим стационарное течение идеальной жидкости. Выделим в стационарно текущей идеальной жидкости трубку тока малого сечения. Рассмотрим объём жидкости V, ограниченный стенками трубки токаи и перпендикулярными к линиям тока сечениями S ₁ и S ₂. За время D t этот объём переместится. В силу непрерывности струи: D V ₁= D V ₂= D V. Энергия каждой частицы жидкости складывается из её кинетической и потенциальной энергии. Вследствие стационарности течения приращение энергии D Е всего рассматриваемого объёма V можно вычислить как разность энергий заштрихованных объёмов D V ₁ и D V ₂. 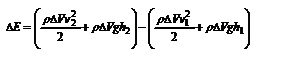где r - плотность жидкости. В идеальной жидкости приращение энергии должно равняться работе, совершаемой над выделенным объёмом силами давления: D Е = А (1), А = P ₁ S ₁D l ₁ - P ₂ S ₂D l ₂ = (P ₁ - P ₂ ) D V. Подставляя в (1) и сократив DV, получим: 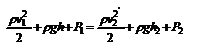^. Поскольку сечения S ₁ и S ₂ произвольные, то это справедливо в любом сечении трубки тока. В стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие: 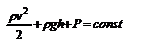– уравнение Бернулли. Для горизонтальной линии тока уравнение Бернулли примет вид: 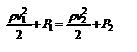, т.е. давление оказывается меньшим в тех точках, где скорость больше.

Рассмотрим 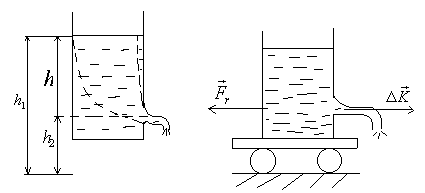истечение жидкости из небольшого отверстия в широком открытом сосуде. Выделим в жидкости трубку тока, имеющую своим сечением с одной стороны открытую поверхность, а с другой стороны – отверстие, через которое вытекает жидкость. P ₁ = P ₂ – давления в обоих сечениях равны атмосферному. Скорость перемещения открытой поверхности в широком сосуде положим, равна нулю. Тогда: 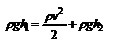, где v – скорость течения из отверстия. Отсюда: 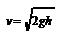- формула Торричелли, где h = h ₁ - h ₂. 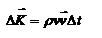-импульс силы. 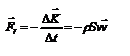- реакция вытекающей струи.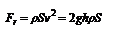

Течение жидкости по трубе. Формула Пуазейля. 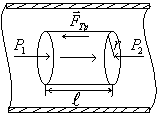Пологая течение жидкости ламинарным, найдём закон изменения скорости v с расстоянием r от оси трубы, т.е. v(r) -? Выделим воображаемый цилиндрический объём жидкости радиуса r и длинны l. Поскольку скорости всех частиц жидкости являются постоянными v = const, сумма внешних сил, приложенных к любому объёму жидкости, равна нулю. На основание цилиндра действуют силы давления, сумма которых равна: 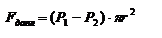. На боковую поверхность цилиндра действует сила трения: 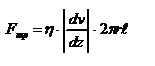. Поскольку 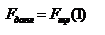, то 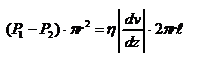. Учитывая, что скорость убывает с расстоянием от оси трубы, т.е. 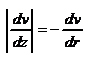, из (1) получим: 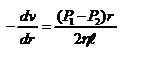, 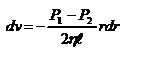. Интегрирование даёт: 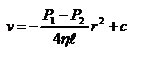. Так как при r = R скорость v = 0, то 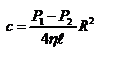, где R - радиус трубы.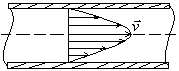 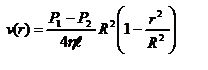- закон изменения скорости жидкости от расстояния до оси трубы. Если 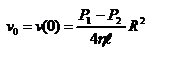- скорость на оси трубы, то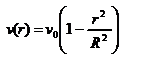 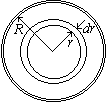Вычислим поток жидкости Q – т. е. объём жидкости, протекающей через поперечное сечение трубы за единицу времени. Для этого сначала определим поток жидкости через кольцо радиуса r и толщиной dr: 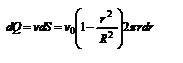-поток жидкости через кольцо dr. Интегрируя по r, получим поток жидкости через поперечное сечение трубы: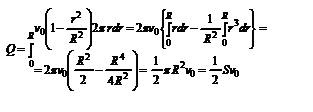 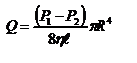- формула Пуазеля. Ее можно использовать для определения коэффициента вязкости .

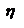25. Вязкость. Ламинарное течение в трубе. Формула Пуазейля. Турбулентное течение жидкости. Число Рейнольдса.

Гидродинамика вязкой жидкости. Коэффициент вязкости. Ламинарные и турбулентные течения. Всем реальным жидкостям и газам присуща вязкость или внутреннее трение. Вязкость проявляется в том, что возникшее в жидкости или газе движение после прекращения действия причин, его вызвавших, постепенно прекращается. Рассмотрим следующий опыт: 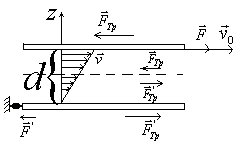В жидкость погружены две параллельные друг другу пластины, линейные размеры которых значительно превосходят расстояние между ними d. Нижняя пластина удерживается на месте, верхняя приводится в движение относительно нижней с некоторой скоростью 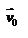под действием постоянной силы 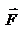. Пусть S - площадь поверхности пластин, тогда 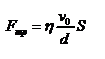-- сила трения, действующая на пластину при ее движении, где h- коэффициент внутреннего трения или коэффициент вязкости. Опыт показывает, что 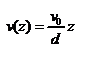- скорость частиц жидкости в разных слоях. Так как 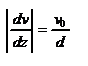- модуль градиента скорости. 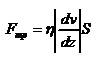- сила внутреннего трения между слоями жидкости при ее движении. Размерность коэффициент вязкости: в СИ 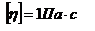, в СГС 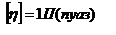. 1 Па с =10 П. У жидкостей коэффициент вязкости h уменьшается с увеличением температуры, у газов наоборот. Наблюдается два вида течения жидкости (газа):

1) Ламинарное (слоистое) течение - течение, при котором жидкость как бы разделяется на слои, которые скользят друг относительно друга, не перемешиваясь.

2) Турбулентное течение – течение, при котором возникает сильное перемешивание жидкости. Течение жидкости при этом нестационарное.

Английский учёный Рейнольдс установил, что характер течения жидкости зависит от значения безразмерной величины: 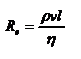- число Рейнольдса, где l характерный для поперечного сечения размер. Как видно из этого выражения, имеет смысл ввести новую характеристику вязкой жидкости: 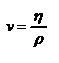- кинематический коэффициент вязкости.

Дата добавления: 2015-04-23