
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кривые распределения и критерии согласия
|
|
|
|
7.3.
Основной целью анализа вариационных рядов является выявление закономерности распределения, исключая при этом влияние случайных для данного распределения факторов. Этого можно достичь, если увеличивать объем исследуемой совокупности и одновременно уменьшать интервал ряда. При попытке изображения этих данных графически мы получим некоторую плавную кривую линию, которая для полигона частот будет являться некоторым пределом. Эту линию называют кривой распределения.
Иными словами,  кривая распределения есть графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, которое функционально связано с изменением вариант. Кривая распределения отражает закономерность изменения частот при отсутствии случайных факторов. Графическое изображение облегчает анализ рядов распределения [Литература: 2. C. 115-119, 138-144].
кривая распределения есть графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, которое функционально связано с изменением вариант. Кривая распределения отражает закономерность изменения частот при отсутствии случайных факторов. Графическое изображение облегчает анализ рядов распределения [Литература: 2. C. 115-119, 138-144].
Известно достаточно много форм кривых распределения, по которым может выравниваться вариационный ряд, но в практике статистических исследований наиболее часто используются такие формы, как нормальное распределение и распределение  Пуассона.
Пуассона.
Нормальное распределение зависит от двух параметров: средней арифметической  и среднего квадратического отклонения
и среднего квадратического отклонения 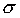 . Его кривая выражается уравнением
. Его кривая выражается уравнением
 (7.6)
(7.6)
где у - ордината кривой нормального распределения; 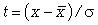 - стандартизованные отклонения; е и π - математические постоянные; x - варианты вариационного ряда;
- стандартизованные отклонения; е и π - математические постоянные; x - варианты вариационного ряда;  - их средняя величина;
- их средняя величина; 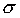 - cреднее квадратическое отклонение.
- cреднее квадратическое отклонение.
Если нужно получить теоретические частоты f' при выравнивании вариационного ряда по кривой нормального распределения, то можно воспользоваться формулой
 (7.7)
(7.7)
где  - сумма всех эмпирических частот вариационного ряда; h - величина интервала в группах;
- сумма всех эмпирических частот вариационного ряда; h - величина интервала в группах; 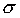 - cреднее квадратическое отклонение;
- cреднее квадратическое отклонение; 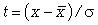 - нормированное отклонение вариантов от средней арифметической; все остальные величины легко вычисляются по специальным таблицам.
- нормированное отклонение вариантов от средней арифметической; все остальные величины легко вычисляются по специальным таблицам.
При помощи этой формулы мы получаем теоретическое (вероятностное) распределение, заменяя им эмпирическое (фактическое) распределение, по характеру они не должны отличаться друг от друга.
Тем не менее в ряде случаев, если вариационный ряд представляет собой распределение по дискретному признаку, где при увеличении значений признака х частоты начинают резко уменьшаться, а средняя арифметическая, в свою очередь, равна или близка по значению к дисперсии (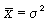 ), такой ряд выравнивается по кривой
), такой ряд выравнивается по кривой  Пуассона [Литература: 5. С. 45].
Пуассона [Литература: 5. С. 45].
 Кривую Пуассона можно выразить отношением
Кривую Пуассона можно выразить отношением
 (7.8)
(7.8)
где Px - вероятность наступления отдельных значений х; 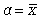 - средняя арифметическая ряда.
- средняя арифметическая ряда.
При выравнивании эмпирических данных теоретические частоты можно определить по формуле
 (7.9)
(7.9)
где f' - теоретические частоты; N - общее число единиц ряда.
Сравнивая полученные величины теоретических частот f' c эмпирическими (фактическими) частотами f, убеждаемся, что их расхождения могут быть весьма невелики.
Объективная характеристика соответствия теоретических и эмпирических частот может быть получена при помощи специальных статистических показателей, которые называют критериями согласия.
Для оценки близости эмпирических и теоретических частот применяются критерий согласия Пирсона, критерий согласия Романовского, критерий согласия Колмогорова.
Наиболее распространенным является  критерий согласия
критерий согласия  К. Пирсона
К. Пирсона  , который можно представить как сумму отношений квадратов расхождений между f' и f к теоретическим частотам:
, который можно представить как сумму отношений квадратов расхождений между f' и f к теоретическим частотам:
 (7.10)
(7.10)
Вычисленное значение критерия  необходимо сравнить с табличным (критическим) значением
необходимо сравнить с табличным (критическим) значением  . Табличное значение определяется по специальной таблице, оно зависит от принятой вероятности Р и числа степеней свободы k (при этом k = m - 3, где m - число групп в ряду распределения для нормального распределения). При расчете критерия согласия Пирсона должно соблюдаться следующее условие: достаточно большим должно быть число наблюдений (n
. Табличное значение определяется по специальной таблице, оно зависит от принятой вероятности Р и числа степеней свободы k (при этом k = m - 3, где m - число групп в ряду распределения для нормального распределения). При расчете критерия согласия Пирсона должно соблюдаться следующее условие: достаточно большим должно быть число наблюдений (n 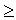 50), при этом если в некоторых интервалах теоретические частоты < 5, то интервалы объединяют для условия > 5.
50), при этом если в некоторых интервалах теоретические частоты < 5, то интервалы объединяют для условия > 5.
Если  , то расхождения между эмпирическими и теоретическими частотами распределения могут быть случайными и предположение о близости эмпирического распределения к нормальному не может быть отвергнуто.
, то расхождения между эмпирическими и теоретическими частотами распределения могут быть случайными и предположение о близости эмпирического распределения к нормальному не может быть отвергнуто.
В том случае, если отсутствуют таблицы для оценки случайности расхождения теоретических и эмпирических частот, можно использовать  критерий согласия
критерий согласия  В.И. Романовского КРом, который, используя величину
В.И. Романовского КРом, который, используя величину  , предложил оценивать близость эмпирического распределения кривой нормального распределения при помощи отношения
, предложил оценивать близость эмпирического распределения кривой нормального распределения при помощи отношения
 (7.11)
(7.11)
где m - число групп; k = (m - 3) - число степеней свободы при исчислении частот нормального распределения.
Если вышеуказанное отношение < 3, то расхождения эмпирических и теоретических частот можно считать случайными, а эмпирическое распределение - соответствующим нормальному. Если отношение > 3, то расхождения могут быть достаточно существенными и гипотезу о нормальном распределении следует отвергнуть.
 Критерий согласия
Критерий согласия  А.Н. Колмогорова
А.Н. Колмогорова  используется при определении максимального расхождения между частотами эмпирического и теоретического распределения, вычисляется по формуле
используется при определении максимального расхождения между частотами эмпирического и теоретического распределения, вычисляется по формуле
 (7.12)
(7.12)
где D - максимальное значение разности между накопленными эмпирическими и теоретическими частотами;  - сумма эмпирических частот.
- сумма эмпирических частот.
По таблицам значений вероятностей  -критерия можно найти величину
-критерия можно найти величину  , соответствующую вероятности Р. Если величина вероятности Р значительна по отношению к найденной величине
, соответствующую вероятности Р. Если величина вероятности Р значительна по отношению к найденной величине  , то можно предположить, что расхождения между теоретическим и эмпирическим распределениями несущественны.
, то можно предположить, что расхождения между теоретическим и эмпирическим распределениями несущественны.
Необходимым условием при использовании критерия согласия Колмогорова является достаточно большое число наблюдений (не меньше ста).
Первым этапом статистического изучения вариации являются построение вариационного ряда -упорядоченного распределения единиц совокупности по возрастающим (чаще) или поубывающим (реже) значениям признака и подсчет числа единиц с тем или иным значениемпризнака.
Существуют три формы вариационного ряда: ранжированный ряд, дискретный ряд,интервальный ряд. Вариационный ряд часто назы-вают рядом распределения. Этот терминиспользуется при изучении вариации как количественных, так и неколичественных признаков.Ряд распределения представляет собой структурную группировку (см. гл. 6).
Ранжированный ряд — это перечень отдельных единиц совокупности в порядке возрастания(убывания) изучаемого признака.
Примером ранжированного ряда может служить табл. 5.5.
Таблица 5.5
Крупные банки Санкт-Петербурга, ранжированные по размерам
собственного капитала на 01.07.96
| Название банка | Собственный капитал, млрд руб. |
| Петроагропромбанк 71 Петровский 146 Балтийский 196 Банк Санкт-Петербург 201 Промстройбанк 731 |
Если численность единиц совокупности достаточно велика, ранжированный ряд становитсягромоздким, а его построение, даже с помощью ЭВМ, занимает длительное время. В такихслучаях вариационный ряд строится с помощью группировки единиц совокупности по значениямизучаемого признака.
Если признак принимает небольшое число значений, строится дискретный вариационный ряд.Примером такого ряда является распределение футбольных матчей по числу забитых мячей(табл. 5.1). Дискретный вариационный ряд - это таблица, состоящая из двух строк или граф:конкретных значений варьирующего признака хi и числа единиц совокупности с даннымзначением признака fi частот (f - начальная буква англ. слова frequency).
Определение числа групп
Число групп в дискретном вариационном ряду определяется числом реально существующихзначений варьирующего признака. Если же признак может принимать хотя и дискретныезначения, но их число очень велико (например, поголовье скота на 1 января года в разныхсельхозпредприятиях может составлять от нуля до десятков тысяч голов), тогда строитсяинтервальный вариационный ряд. Интервальный вариационный ряд строится и для изученияпризнаков, которые могут принимать любые, как целые, так и дробные, значения в областисвоего существования. Таковы, например, рентабельность реализованной продукции,себестоимость единицы продукции, доход на 1 жителя города, доля лиц с высшим образованиемсреди населения разных территорий и вообще все вторичные признаки, значения которыхрассчитываются путем деления величины одного первичного признака на величину другого (см.гл. 3).
Интервальный вариационный ряд представляет собой таблицу, (состоящую из двух граф (илистрок) — интервалов признака, вариация которого изучается, и числа единиц совокупности,попадающих в данный интервал (частот), или долей этого числа от общей численностисовокупности (частостей).
При построении интервального вариационного ряда необходимо выбрать оптимальное числогрупп (интервалов признака) и установить длину интервала. Поскольку при анализевариационного ряда сравнивают частоты в разных интервалах, необходимо, чтобы величинаинтервала была постоянной. Оптимальное число групп выбирается так, чтобы в достаточноймере отразилось разнообразие значений признака в совокупности и в то же времязакономерность распределения, его форма не искажалась случайными колебаниями частот. Еслигрупп будет слишком мало, не проявится закономерность вариации; если групп будет чрезмерномного, случайные скачки частот исказят форму распределения.
Чаще всего число групп в вариационном ряду устанавливают, придерживаясь формулы,рекомендованной американским статистиком Стерджессом (Sturgess):

где k - число групп; n - численность совокупности.
Эта формула показывает, что число групп - функция объема данных.
Предположим, необходимо построить вариационный ряд распределения предприятий областипо урожайности зерновых культур за какой-то год. Число сельхозпредприятий, имевших посевызерновых культур, составило 143; наименьшее значение урожайности равно 10,7 ц/га,наибольшее - 53,1 ц/га. Имеем:
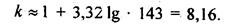
Так как число групп целое, следовательно, рекомендуется построить 8 или 9 групп.
Определение величины интервала
Зная число групп, рассчитывают величину интервала:

В нашем примере величина интервала составляет:
а) при 8 группах
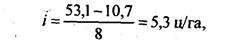
б) при 9 группах

Для построения ряда и анализа вариации значительно лучше иметь по возможностиокругленные значения величины интервала и его границ. Поэтому наилучшим решением будетпостроение вариационного ряда с 9 группами с интервалом, равным 5 ц/га. Этот вариационныйряд приведен в табл. 5.6, а его графическое изображение дано на рис. 5.1.
Границы интервалов могут указываться разным образом: верхняя граница предыдущегоинтервала повторяет нижнюю границу следующего, как показано в табл. 5.6, или неповторяет.
В последнем случае второй интервал будет обозначен как 15,1-20, третий как 20,1-25 и т.д.,т.е. предполагается, что все значения урожайности обязательно округлены до одной десятой.Кроме того, возникает нежелательное осложнение с серединой интер- вала 15,1-20, которая,строго говоря, уже будет равна не 17,5, а 17,55; соответственно при замене округленногоинтервала 40-60 на 40,1-6,0 вместо округленного значения его середины 50 получим 50,5,Поэтому предпочтительнее оставить интервалы с повторяющейся округленной границей идоговориться, что единицы совокупности, имеющие значение признака, равное границеинтервала, включаются в тот интервал, где это точное значение впервые указывается. Так,хозяйство, имеющее урожайность, равную 15 ц/га, включается в первую группу, значение 20ц/га -во вторую и т. д.

Рис. 5.1. Распределение хозяйств по урожайности
Таблица 5.6
Распределение хозяйств области по урожайности зерновых культур
| Группы хозяйств поурожайности, ц/га хj | Число хозяйств fj | Серединаинтервала, ц/га хj' | x’j | Накопленнаячастота f’j |
| 10- 15 | 12,5 | 75,0 | б | |
| 15-20 | 17,5 | 157,5 | ||
| 20-25 | 22,5 | 450,0 | ||
| 25 -30 | 27,5 | 1127,5 | ||
| 30-35 | 32,5 | 845,0 | ||
| 35-40 | 37,5 | 787,5 | ||
| 40-45 | 42,5 | 595,0 | ||
| 45 - 50 | 47,5 | 23-7,5 | ||
| 50-55 | 52,5 | 52,5 | ||
| Итого | 4327,5 |
Графическое изображение вариационного ряда
Существенную помощь в анализе вариационного ряда и его свойств оказывает графическоеизображение. Интервальный ряд изображается столбиковой диаграммой, в которой основаниястолбиков, расположенные на оси абсцисс, — это интервалы значений варьирующего признака,а высоты столбиков - частоты, -соответствующие масштабу по оси ординат. Графическоеизображение распределения хозяйств области по урожайности зерновых культур приведено нарис. 5.1. Диаграмма этого рода часто называется гистограммой (от греческого слова «гистос» -ткань, строение).
Данные табл. 5.5 и рис. 5.1 показывают характерную для многих признаков формураспределения: чаще встречаются значения средних интервалов признака, реже - крайние;малые и большие значения признака. Форма этого распределения близка к рассматриваемому вкурсе математической статистики закону нормального распределения. Великий русскийматематик А. М. Ляпунов (1857 - 1918) доказал, что нормальное распределение образуется,если на варьирующую переменную влияет большое число факторов, ни один из которых неимеет преобладающего влияния. Случайное сочетание множества примерно равных факторов,влияющих на вариацию урожайности зерновых культур, как природных, так иагротехнических, экономических, создает близкое к нормальному закону распределенияраспределение хозяйств области по урожайности.
Если имеется дискретный вариационный ряд или используются середины интервалов, тографическое изображение такого вариационного ряда называется полигоном (от греч. слова -многоугольник). Каждый из вас легко построит этот график, соединяя прямыми точки скоординатами х, и /.
Отношение высоты полигона или диаграммы к их основанию рекомендуется в пропорциипримерно 5:8.
Понятие частости
Если в табл. 5.6 число хозяйств с тем или иным уровнем урожайности выразить в процентах китогу, принимая все число хозяйств (143) за 100%, то средняя урожайность может бытьвычислена так:

где w - частость 7-й категории вариационного ряда;
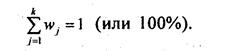
Кумулятивное распределение
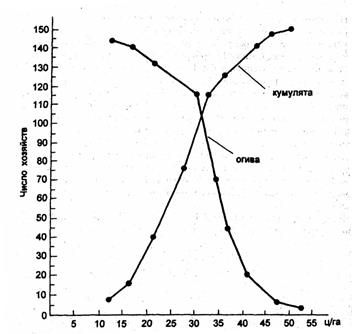
Преобразованной формой вариационного ряда является ряд накопленных частот, приведенныйв табл. 5.6, графа 5. Это ряд значений числа единиц совокупности с меньшими и равныминижней границе соответствующего интервала значениями признака. Такой ряд называетсякумулятивным. Можно построить кумулятивное распределение «не меньше, чем», а можно«больше, чем». В первом случае график кумулятивного распределения называется кумулятой,во втором - огивой (рис. 5.2).
Плотность, распределения
Если приходится иметь дело с вариационным рядом с неравными интервалами, то длясопоставимости нужно частоты или частости привести к единице интервала. Полученноеотношение называется плотностью распределения:


Плотность распределения используется как для расчета обобщающих показателей, так и дляграфического изображения вариационных рядов с неравными интервалами.
24.
Одной из простейших мер вариации является размах или колеблемость варьирующего признака: 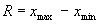 , но он не описывает вариацию признака внутри интервала [xmax; xmin]. Такой характеристикой, которая дает обобщенную характеристику ряда и гасит случайные отклонения значений признака, является средняя. Вокруг значения средней величины происходят колебания признака, для обобщения этих колебаний применяется средняя величина этих отклонений:
Среднее линейное отклонение для арифметической простой , но он не описывает вариацию признака внутри интервала [xmax; xmin]. Такой характеристикой, которая дает обобщенную характеристику ряда и гасит случайные отклонения значений признака, является средняя. Вокруг значения средней величины происходят колебания признака, для обобщения этих колебаний применяется средняя величина этих отклонений:
Среднее линейное отклонение для арифметической простой
 (11)
при исчислении средней величины по формуле простой средней арифметической.
Среднее линейное отклонение для арифметической взвешенной (11)
при исчислении средней величины по формуле простой средней арифметической.
Среднее линейное отклонение для арифметической взвешенной
 (12)
при исчислении средней величины признака по формуле средней арифметической взвешенной.
При достаточно большом размахе величина линейного отклонения достигает или превышает среднее значение признака. При различии максимального и минимального значения признака на порядок или более эта характеристика не описывает характер вариации. Для такого описания применяют средний квадрат отклонений от средней величины или дисперсию и среднее квадратическое отклонение, которое является корнем второй степени из дисперсии.
Среднее квадратическое отклонение для не сгруппированных данных (12)
при исчислении средней величины признака по формуле средней арифметической взвешенной.
При достаточно большом размахе величина линейного отклонения достигает или превышает среднее значение признака. При различии максимального и минимального значения признака на порядок или более эта характеристика не описывает характер вариации. Для такого описания применяют средний квадрат отклонений от средней величины или дисперсию и среднее квадратическое отклонение, которое является корнем второй степени из дисперсии.
Среднее квадратическое отклонение для не сгруппированных данных
 (13)
это средний квадрат отклонений от средней или дисперсия, которая описывает структуру совокупности. (13)
это средний квадрат отклонений от средней или дисперсия, которая описывает структуру совокупности.
 (14)
среднее квадратическое отклонение от средней величины признака.
Среднее квадратическое отклонение для сгруппированных данных (14)
среднее квадратическое отклонение от средней величины признака.
Среднее квадратическое отклонение для сгруппированных данных
 (15)
средний квадрат отклонений от средней или дисперсия; (15)
средний квадрат отклонений от средней или дисперсия;
 (16)
среднее квадратическое отклонение от средней.
Такие характеристики вариации признака, как средняя величина и среднее квадратическое отклонение для интервальных рядов с равными интервалами могут быть рассчитаны по способу моментов:
Среднее значение изучаемого признака по способу моментов (16)
среднее квадратическое отклонение от средней.
Такие характеристики вариации признака, как средняя величина и среднее квадратическое отклонение для интервальных рядов с равными интервалами могут быть рассчитаны по способу моментов:
Среднее значение изучаемого признака по способу моментов
 (17)
Средний квадрат отклонений по способу моментов (17)
Средний квадрат отклонений по способу моментов
 (18)
где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой),
h – шаг интервала, (18)
где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой),
h – шаг интервала,
 (19)
Коэффициент вариации (19)
Коэффициент вариации
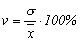 . (20)
Величина коэффициента вариации говорит об однородности изучаемой совокупности, так, если вариация меньше либо равняется 33%, то совокупность считается однородной. Формулы, используемые для расчёта среднего линейного отклонения, – средняя арифметическая простая и взвешенная. Для расчёта среднего квадратического отклонения и коэффициента вариации применяется формула средней квадратической. . (20)
Величина коэффициента вариации говорит об однородности изучаемой совокупности, так, если вариация меньше либо равняется 33%, то совокупность считается однородной. Формулы, используемые для расчёта среднего линейного отклонения, – средняя арифметическая простая и взвешенная. Для расчёта среднего квадратического отклонения и коэффициента вариации применяется формула средней квадратической.
| ||||||||||||||||||||||||||
| 6. Построение линейной парной корреляции | ||||||||||||||||||||||||||
Для изучения взаимодействия признаков используют исследования по типам связей между различными явлениями и их признаками. Различают два типа связей:
Типы связей между статистическими признаками
Определение: Корреляционной связью называется такая связь между явлениями и их признаками, когда разным значениям переменной соответствуют различные значения условной средней величины другой переменной. Корреляционная связь является частным случаем статистической. Для изучения корреляционных связей используют уравнение регрессии, которое представляет собой математическое выражение связи признаков, базирующееся на изменении условной средней величины результативного признака с изменением факторного признака (факторный признак – признак, оказывающий влияние на другие признаки, результативный признак – признак, испытывающий на себе влияние факторного). Уравнение регрессии, выраженное функцией (линейной или нелинейной) и описывающее зависимость результативного признака от одного факторного – уравнение парной регрессии, а описывающее зависимость результативного от нескольких факторных признаков – уравнение множественной регрессии, то есть регрессионная модель основана на аналитическом представлении связи факторного и результативного признаков. Простейшим уравнением парной корреляции (регрессии) является линейное уравнение: где b – вариация результативного признака на единицу факторного, a – теоретическое значение результативного признака при значении факторного, равное 0 (x=0), что на практике не имеет никакого экономического смысла. Для вычисления параметров a и b решается система уравнений:
Можно применять для расчёта параметров формулу: тогда При линейной корреляционной связи применяют показатель тесноты связи между изучаемыми признаками – коэффициент корреляции: линейный коэффициент детерминации: Равенство этих коэффициентов говорит об адекватности построенной модели, то есть о соответствии построенной модели существующей между признаками зависимости. Коэффициент детерминации ( Таблица 4
| ||||||||||||||||||||||||||
Дисперсия — это средний квадрат отклонения индивидуальных значений признака от средней арифметической. В зависимости от исходных данных она вычисляется по формулам простой и взвешенной дисперсий:
1. ^ Простая дисперсия (для несгруппированных данных) вычисляется по формуле:
σ2 =Σ(x i - x)2/n
2. Взвешенная дисперсия (для вариационного ряда):
σ2 =Σ(x i - x)2x fi/∑ fi
^ Среднее квадратичное отклонение представляет собой обобщающую характеристику размеров вариации признака в совокупности. Оно равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической и может быть вычислено следующим образом:
σ = √σ2
Среднее квадратичное отклонение показывает, на сколько, в среднем, отклоняются конкретные варианты от их среднего значения, а также является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому хорошо интерпретируется.
Порядок расчета среднего квадратического отклонения на основе вариационного ряда таков:
1) находим среднюю арифметическую ряда (х);
2) находим отклонение каждого варианта от средней арифметической
(x i - x);
3) возводим каждое отклонение в квадрат: (x i - x)2,
4) умножаем каждый квадрат отклонений на соответствующие веса:
(x i - x)2 x fi
5) суммируем все произведения: Σ(x i - x)2х fi
6) разделив указанную выше сумму произведений на сумму весов (частот или частостей), получаем дисперсию.
σ2=Σ(x i - x)2´ fi / ∑ fi
7) извлекая квадратный корень из дисперсии, получаем стандартное отклонение
___
σ = √σ2
Таким образом, основой для расчета стандартного отклонения является дисперсия
25. Мода - это наиболее часто встречающееся в совокупности значение признака. Для дискретного вариационного ряда мода определяется по частотам вариант и соответствует варианте с максимальной частотой.
Особенности применения моды:
1) если все значения вариационного ряда имеют одинаковую частоту, то говорят, что этот вариационный ряд не имеет моды;
2) если две соседних варианты имеют одинаковую доминирующую частоту, то мода вычисляется как среднее арифметическое этих вариант;
3) если две несоседних варианты имеют одинаковую доминирующую частоту, то такой вариационный ряд называется бимодальным;
4) если таких вариант более двух, то ряд полимодальный.
Определение модального интервала в случае интервального вариационного ряда:
1) с равными интервалами модальный интервал определяется по наибольшей частоте;
2) при неравных интервалах - по наибольшей плотности.
Формула определения моды при равных интервалах внутри модального интервала:

Применение моды:
1) в практике мода и медиана иногда используются вместо средней арифметической или вместе с ней;
2) фиксируя средние цены товаров или продуктов на рынке, записывают наиболее часто встречающуюся цену на рынке (моду цены).
|
|
|
|
|
Дата добавления: 2015-04-23; Просмотров: 1290; Нарушение авторских прав?; Мы поможем в написании вашей работы!

 (21)
(21) – условное среднее значение результативного признака,
– условное среднее значение результативного признака,
 (22)
(22) , (23)
, (23) .
. , (24)
, (24) , (25)
, (25) – средние значения факторного и результативного признаков,
– средние значения факторного и результативного признаков, – условная средняя величина результативного признака, рассчитанная на основе аналитической зависимости от фактора.
– условная средняя величина результативного признака, рассчитанная на основе аналитической зависимости от фактора. ), выраженный в процентах, показывает, какая часть изменений результативного признака обусловлена изменениями факторного (тесноту связи):
), выраженный в процентах, показывает, какая часть изменений результативного признака обусловлена изменениями факторного (тесноту связи):  . Величина коэффициента корреляции колеблется в пределах:
. Величина коэффициента корреляции колеблется в пределах: 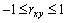 и показывает силу связи, которую можно определить по шкале Чеддока:
и показывает силу связи, которую можно определить по шкале Чеддока: