Билет№26. Императивные, функциональные и логические языки программирования

Интерпретатор — это программа, обеспечивающая перевод с алгоритмического языка высокого уровня на машинный с одновременным выполнениемоператоров программы. Трансляция программы — преобразование программы, представленной на одном из языков программирования, в программу на другом языке и, в определённом смысле, равносильную первой. Язык, на котором представлена входная программа, называется исходным языком, а сама программа — исходным кодом. Выходной язык называется целевым языком или объектным кодом.

Языки программирования принадлежат трем классам:1)интеративный(процедурные)- это парадигма программирования, которая, в отличие от декларативного программирования, описывает процесс вычисления в виде инструкций, изменяющих состояние программы. Императивная программа очень похожа на приказы, выражаемые повелительным наклонением в естественных языках, то есть это последовательность команд, которые должен выполнить компьютер. Императивные языки программирования противопоставляются функциональным и логическим языкам программирования. Функциональные языки, например, Haskell, не представляют собой последовательность инструкций и не имеют глобального состояния. Логические языки программирования, такие как Prolog, обычно определяют что надо вычислить, а не как это надо делать. Функциона́льное программи́рование(LISP, HASKEL) — раздел дискретной математики и парадигма программирования, в которой процесс вычисления трактуется как вычисление значений функций в математическом понимании последних (в отличие от функций как подпрограмм в процедурном программировании). При необходимости, в функциональном программировании вся совокупность последовательных состояний вычислительного процесса представляется явным образом, например как список.Функциональное программирование предполагает обходиться вычислением результатов функций от исходных данных и результатов других функций, и не предполагает явного хранения состояния программы. Соответственно, не предполагает оно и изменяемость этого состояния (в отличие от императивного, где одной из базовых концепций является переменная, хранящая своё значение и позволяющая менять его по мере выполнения алгоритма). На практике отличие математической функции от понятия «функции» в императивном программировании заключается в том, что императивные функции могут опираться не только на аргументы, но и на состояние внешних по отношению к функции переменных, а также иметь побочные эффекты и менять состояние внешних переменных. Таким образом, в императивном программировании при вызове одной и той же функции с одинаковыми параметрами, но на разных этапах выполнения алгоритма, можно получить разные данные на выходе из-за влияния на функцию состояния переменных. А в функциональном языке при вызове функции с одними и теми же аргументами мы всегда получим одинаковый результат: выходные данные зависят только от входных. Это позволяет средам выполнения программ на функциональных языках кэшировать результаты функций и вызывать их в порядке, не определяемом алгоритмом. Логи́ческое программи́рование(алгоритма нет, объявление неких фактов) — парадигма программирования, основанная на автоматическом доказательстве теорем, а также раздел дискретной математики, изучающий принципы логического вывода информации на основе заданных фактов и правил вывода. Логическое программирование основано на теории и аппарате математической логики с использованием математических принципов резолюций. Самым известным языком логического программирования является Prolog. Первым языком[источник не указан 971 день] логического программирования был язык Planner, в котором была заложена возможность автоматического вывода результата из данных и заданных правил перебора вариантов (совокупность которых называлась планом). Planner использовался для того, чтобы понизить требования к вычислительным ресурсам (с помощью метода backtracking) и обеспечить возможность вывода фактов, без активного использования стека. Затем был разработан язык Prolog, который не требовал плана перебора вариантов и был, в этом смысле, упрощением языка Planner.

Билет№27 Парадигмы программирования. Подпрограммы, модульность, структурные программирования, объективно ориентировочные программирования.

Паради́гма программи́рования — это совокупность идей и понятий, определяющих стиль написания программ. Парадигма в первую очередь определяется базовой программной единицей и самим принципом достижения модульности программы. Важно отметить, что парадигма программирования не определяется однозначно языком программирования — многие современные языки программирования являются мультипарадигменными, то есть допускают использование различных парадигм. Так на языке Си, который не является объектно-ориентированным, можно писать объектно-ориентированным образом, а на Ruby, в основу которого в значительной степени положена объектно-ориентированная парадигма, можно писать согласно стилю функционального программирования. Парадигмы программирования: -модульные программирования, -структурные программирования, -объектно-ориентированное программирование, -визуальное программирование, -событийно-управляемое программирование. Подпрограммы- это программные единицы, которые имеют имя, по которому она может быть вызвана из других частей программ. В простейшем случае (в ассемблерах) подпрограмма представляет собой последовательность команд (операторов), отдельную от основной части программы и имеющую в конце специальную команду выхода из подпрограммы. Обычно подпрограмма также имеет имя, по которому её можно вызвать, хотя ряд языков программирования допускает использование и неименованных подпрограмм. В языках высокого уровня описание подпрограммы обычно состоит по меньшей мере из двух частей: заголовка и тела. Заголовок подпрограммы описывает её имя и, возможно, параметры, то есть содержит информацию, необходимую для вызова подпрограммы. Тело — набор операторов, который будет выполнен всякий раз, когда подпрограмма будет вызвана. Вызов подпрограммы выполняется с помощью команды вызова, включающей в себя имя подпрограммы. В большинстве современных языков программирования команда вызова представляет собой просто имя вызываемой подпрограммы, за которым могут следовать фактические параметры. Модульность в языках программирования — принцип, согласно которому программное средство (ПС, программа, библиотека, web-приложение и др.) разделяется на отдельные именованные сущности, называемые модулями. Модульность часто является средством упрощения задачи проектирования ПС и распределения процесса разработки ПС между группами разработчиков. При разбиении ПС на модули для каждого модуля указывается реализуемая им функциональность, а также связи с другими модулями. Роль модулей могут играть структуры данных, библиотеки функций, классы, сервисы и др. программные единицы, реализующие некоторую функциональность и предоставляющие интерфейс к ней. Структу́рное программи́рование — методология разработки программного обеспечения, в основе которой лежит представление программы в виде иерархической структуры блоков. Предложена в 70-х годах XX века Э. Дейкстрой, разработана и дополнена Н. Виртом В соответствии с данной методологией:1) Любая программа представляет собой структуру, построенную из трёх типов базовых конструкций: последовательное исполнение, ветвление, цикл. 2)Повторяющиеся фрагменты программы могут оформляться в виде подпрограмм (процедур или функций). 3) Разработка программы ведётся пошагово, методом «сверху вниз». Объе́ктно-ориенти́рованное, программи́рование (объект(свойства и методы) и класс)— парадигма программирования, в которой основными концепциями являются понятия объектов и классов. 1)Инкапсуляция(объединение данных и методов их обработки). 2)Наследование.3)Полиморфизм(многообразие)-свойство и методы можно обозначать одним именем. Сигнатура - кол-во и тип параметров.

Билет№28 Этапы разработки программы тестирования. Откладка. Верификация.

Этапы:1)Постановка задач: 1.определение требований к программе.2.определить цели программы.3.разработать внешние спец верификации. 2)Выбор математической модели.3)разработка алгоритма - доказать правильность алгоритма.4)Выбор системы программирования.5)Реализация алгоритма в виде программы.6)Тестирование программы(просто находит ошибку)-выявить («поломать программу») все ошибки.7)Откладка программы(нахождение и исправление ошибки)- исправление ошибок, но в этой программе, мы не найдем где ошибка..8)эксплуатация.9)сопровождение и модификация. Верификация — проверка, проверяемость, способ подтверждения, проверка с помощью доказательств, каких-либо теоретических положений, алгоритмов, программ и процедур путем их сопоставления с опытными (эталонными или эмпирическими) данными, алгоритмами и программами. Отла́дка — этап разработки компьютерной программы, на котором обнаруживают, локализуют и устраняют ошибки. Чтобы понять, где возникла ошибка, приходится:1)узнавать текущие значения переменных;2)выяснять, по какому пути выполнялась программа. Существуют две взаимодополняющие технологии отладки.1)Использование отладчиков — программ, которые включают в себя пользовательский интерфейс для пошагового выполнения программы: оператор за оператором, функция за функцией, с остановками на некоторых строках исходного кода или при достижении определённого условия. 2)Вывод текущего состояния программы с помощью расположенных в критических точках программы операторов вывода — на экран, принтер, громкоговоритель или в файл. Вывод отладочных сведений в файл называется журналированием.

Билет№29 Оценка эффективности нерекурсивных алгоритмов. пример.

Билет№30 Оценка эффективности рекурсивных алгоритмов. пример.

Рекурсивный алгоритм - алгоритм, в тексте которого явно или неявно содержится обращение к самому себе при выполнении некоторого условия. В программировании рекурсия — вызов подпрограммы из неё же самой, непосредственно (простая рекурсия) или через другие подпрограммы (косвенная рекурсия). Пример. Функция A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии. План-анализ эффективности рекурсивных алгоритмов.1) Выберите параметр(ы). по которым будет оцениваться размер входных данных алгоритма.2)Определите основную операцию алгоритма.3)Проверить зависит ли число выполняемых основных операций только от размеров входных данных, если оно зависит от других факторов, рассмотрите при необходимости, как меняется эффективность алгоритма для наихудшего, среднего и наилучшего случая.4)Составить реккурентное уравнение, выражающее кол-во выполняемых и основных операций алгоритма, указать соответствующие начальные условия.5)найти решение реккурентного уравнения или если это невозможно определить хотя бы его порядок роста. Пример, в тетрадке!!

Билет № 31 Реккурентные соотношения. Решения методом обратной подстановки.

Рекуррентное соотношение - это соотношение(равенство, система равентсв) позволяющее свести решение комбинационной задачи для некоторого числа предметов к аналогичной задаче с меньшей размерностью. Решение комбинационных задач с помощью рекуррентных соотношений - это метод рекуррентных соотношений. Рекуррентным соотношением, связывающим элемент последовательности с одним или несколькими другими элементами последовательности, в комбинации с одним или несколькими явными значениями первых элементов (начальными условиями). Пример. x(0) = 0 // начальное условие, x(n) = x(n-1) + 2, n > 0 // рекуррентное соотношение, 0, 2, 4, … // последовательность. Рекуррентные соотношения важны для анализа рекурсивных алгоритмов. Решить рекуррентное соотношение при заданных начальных условиях означает найти явную формулу, которая удовлетворяет как начальным условиям, так и рекуррентному соотношению, либо доказать что данная формула не существует. Метод обратной подстановки:

M(n)=M(n-1)+1 (на другой строке/)/ M(n-1)=M(n-2)+1 / M(n-2)=M(n-3)+1 /…./M(n)=M(n-2)+1+1 / =M(n-3)+3 / =M(n-4)+4 / M(n)=M(n-k)+k / k=n/ M(n-n)=M(0) / M(n)=n

Билет№32 Основные функции, используемые в оценках алгоритма.

Билет №33 Алгоритм сортировки методом пузырька.

Сортировка простыми обменами, сортиро́вка пузырько́м — простой алгоритм сортировки. Для понимания и реализации этот алгоритм — простейший, но эффективен он лишь для небольших массивов. Сложность алгоритма: O(n²). Алгоритм состоит в повторяющихся проходах по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется обмен элементов. Проходы по массиву повторяются до тех пор, пока на очередном проходе не окажется, что обмены больше не нужны, что означает — массив отсортирован. При проходе алгоритма, элемент, стоящий не на своём месте, «всплывает» до нужной позиции как пузырёк в воде, отсюда и название алгоритма. Возьмём массив с числами «5 1 4 2 8» и отсортируем значения по возрастанию, используя сортировку пузырьком. Выделены те элементы, которые сравниваются на данном этапе:

Первый проход:(5 1 4 2 8) (1 5 4 2 8), Здесь алгоритм сравнивает два первых элемента и меняет их местами./(1 5 4 2 8) (1 4 5 2 8), Меняет местами, так как 5 > 4/(1 4 5 2 8) (1 4 2 5 8), Меняет местами, так как 5 > 2/(1 4 2 5 8) (1 4 2 5 8), Теперь, ввиду того, что элементы стоят на своих местах (8 > 5)/ алгоритм не меняет их местами. Второй проход:(1 4 2 5 8) (1 4 2 5 8)/ (1 4 2 5 8) (1 2 4 5 8), Меняет местами, так как 4 > 2/ (1 2 4 5 8) (1 2 4 5 8)/ (1 2 4 5 8) (1 2 4 5 8)Теперь массив полностью отсортирован, но алгоритм не знает так ли это. Поэтому ему необходимо сделать полный проход и определить, что перестановок элементов не было. Третий проход:(1 2 4 5 8) (1 2 4 5 8)/ (1 2 4 5 8) (1 2 4 5 8)/ (1 2 4 5 8) (1 2 4 5 8)/ (1 2 4 5 8) (1 2 4 5 8)/ Теперь массив отсортирован и алгоритм может быть завершён.

Билет№34 Алгоритм сортировки выбором.

Сортировка выбором — алгоритм сортировки. Может быть реализован и как устойчивый и как неустойчивый. На массиве из n элементов имеет время выполнения в худшем, среднем и лучшем случае Θ(n2), предполагая что сравнения делаются за постоянное время. Шаги алгоритма:1)находим минимальное значение в текущем списке2)производим обмен этого значения со значением на первой неотсортированной позиции3)теперь сортируем хвост списка, исключив из рассмотрения уже отсортированные элементы. Идея метода состоит в том, чтобы создавать отсортированную последовательность путем присоединения к ней одного элемента за другим в правильном порядке.Будем строить готовую последовательность, начиная с левого конца массива. Алгоритм состоит из n последовательных шагов, начиная от нулевого и заканчивая (n-1)-м.На i-м шаге выбираем наименьший из элементов a[i]... a[n] и меняем его местами с a[i]. Последовательность шагов при n=5 изображена на рисунке ниже. Вне зависимости от номера текущего шага i, последовательность a[0]...a[i] (выделена курсивом) является упорядоченной. Таким образом, на (n-1)-м шаге вся последовательность, кроме a[n] оказывается отсортированной, а a[n] стоит на последнем месте по праву: все меньшие элементы уже ушли влево. Для нахождения наименьшего элемента из n+1 рассматримаемых алгоритм совершает n сравнений. С учетом того, что количество рассматриваемых на очередном шаге элементов уменьшается на единицу, общее количество операций:n + (n-1) + (n-2) + (n-3) +... + 1 = 1/2 * (n2+n) = Theta(n2).Таким образом, так как число обменов всегда будет меньше числа сравнений, время сортировки растет квадратично относительно количества элементов.Алгоритм не использует дополнительной памяти: все операции происходят "на месте". Пример в тетрадке

Билет№35 Алгоритм линейного поиска.

Линейный, последовательный поиск — алгоритм нахождения заданного значения произвольной функции на некотором отрезке. Данный алгоритм является простейшим алгоритмом поиска и в отличие, например, от двоичного поиска, не накладывает никаких ограничений на функцию и имеет простейшую реализацию. Поиск значения функции осуществляется простым сравнением очередного рассматриваемого значения (как правило поиск происходит слева направо, то есть от меньших значений аргумента к большим) и, если значения совпадают (с той или иной точностью), то поиск считается завершённым.Пример в тетр.

Билет№36 Алгоритм бинарного поиска.

Алгоритм поиска по бинарному дереву.Суть этого алгоритма достаточно проста. Представим себе, что у нас есть набор карточек с телефонными номерами и адресами людей. Карточки отсортированы в порядке возрастания телефонных номеров. Необходимо найти адрес человека, если мы знаем, что его номер телефона 222-22-22. Наши действия? Берем карточку из середины пачки, номер карточки 444-44-44. Сравнивая его с искомым номером, мы видим, что наш меньше и, значит, находится точно в первой половине пачки. Смело откладываем вторую часть пачки в сторону, она нам не нужна, массив поиска мы сузили ровно в два раза. Теперь берем карточку из середины оставшейся пачки, на ней номер 123-45-67. Из чего следует, что нужная нам карточка лежит во второй половине оставшейся пачки... Таким образом, при каждом сравнении, мы уменьшаем зону поиска в два раза. Отсюда и название метода - половинного деления или дихотомии.Не буду приводить математического доказательства, так как это не является целью данной статьи, а просто отмечу, что скорость сходимости этого алгоритма пропорциональна Log(2)N ¹. Это означает буквально то, что не более, чем через Log(2)N сравнений, мы либо найдем нужное значение, либо убедимся в его отсутствии.Другое название этого алгоритма – «метод бинарного дерева» происходит из представления "пути" поиска в виде дерева (у которого каждая следующая ветвь разделяется на две, по одной из которых мы и движемся в дальнейшем)..Способ очень распространенный в наше время, возможно по причине его эффективности вкупе с простотой программирования этого алгоритма. Именно бинарный поиск используется при поиске в индексах таблиц.Есть еще один алгоритм, основанный на делении искомого массива на части, аналогичный предыдущему. Я упомяну о нем скорее из-за некоторой его экзотичности.

Идея этого алгоритма проста(работает на отсортированных массивах\списках):Сначала высчитываем индекс среднего элемента по формуле (m+n)//2.Где n это индекс начального элемента, а m количество элементов в массиве В случае нечетного числа элементов округляем до ближайшего целого полученный результат.А дальше уже смотрим что получается:а) Элемент найден и мы возвращаем его индекс б) Средний элемент меньше ключа поиска в) Средний элемент больше ключа поиска В случае б) мы должны отсечь те элементы которые меньше среднего, то есть правую часть массива\списка. Дробится этого можно приняв за начальную границу поиска первый элемент со значением больше чем средний элемент, а у нас массив\список сортированный значит это элемент с индексом i+1, где i индекс среднего элемента. а конечная граница поиска последний элемент. в случае в) нам нужно принять за начальную границу первый элемент меньший среднего, а значит нам нужен элемент с индексом i-1. Как конечная граница поиска естественно принять индекс первого элемента. Итак весь процесс будем повторять пока не выполниться любое из трех условий:1) Элемент найден 2) Начальная граница стала равна наибольшему элементу массива3) Начальная граница стала равна индексу наименьшего элемента.Самый положительный для нас случай 1.Преимущество алгоритма в том что при каждом сравнении убавляется половина отрезка, где происходит поиск элементов.Краткое описание алгоритма:1. Взять индекс первого элемента (n)2. Взять индекс конечного элемента (длину массива) (m)3. Рассчитать индекс среднего элемента по формуле (m+n)\2 (i) 4. Сравнить средний элемент с ключом4a Пока 0<=i 5а Если ключ = =элементу в выходим из программы 5б Если ключ>элементу,то n=i+1 m=len(l) 5в Если ключ<элементу, то n=i m=i-1 6. Переходим к шагу 4a

Билет №37 Алгоритмы генерации всех перестановок.

Перестановка - это упорядоченный набор элементов. Упорядоченный, это означает, что порядок элементов в наборе имеет значение. И две перестановки, состоящие из одних элементов, расположенных в разном порядке не считаются равными. Известно два алгоритма - рекурсивный и алгоритм лексикографического порядка перестановок. Перестановка (на множестве из n элементов) - биективное отображение множества в себя. Генерация всех перестановок n-элементного множества. Количество различных перестановок множества, состоящего из n элементов равно n!. В этом нетрудно убедиться: на первом месте в перестановке может стоять любой из n элементов множества, после того, как мы на первом месте зафиксировали какой-либо элемент, на втором месте может стоять любой из n – 1 оставшегося элемента и т.д. Таким образом, общее количество вариантов равно n(n – 1)(n – 2)...3?2?1 = n!. То есть рассматривать абсолютно все перестановки мы можем только у множест, состоящих из не более, чем 10 элементов. Рассмотрим рекурсивный алгоритм, реализующий генерацию всех перестановок в лексикографическом порядке. Такой порядок зачастую наимболее удобен при решении олимпиадных задач, так как упрощает применение метода ветвей и границ, который будет описан ниже. Обозначим массив индексов элементов — p. Первоначально он заполнен числами 1, 2,..., n, которые в дальнейшем будут меняться местами. Параметром i рекурсивной процедуры Perm служит место в массиве p, начиная с которого должны быть получены все перестановки правой части этого массива. Идея рекурсии в данном случае следующая: на i-ом месте должны побывать все элементы массива p с i-го по n-й и для каждого из этих элементов должны быть получены все перестановки остальных элементов, начиная с (i+1)-го места, в лексикографическом порядке. После получения последней из перестановок, начиная с (i+1)-го места, исходный порядок элементов должен быть восстановлен.

{описание переменных совпадает с приведенным выше}

procedure Permutations(n:integer);

procedure Perm(i:integer);

var j,k:integer;

begin

if i=n then

begin for j:=1 to n do write(a[p[j]],' '); writeln end

else

begin

for j:=i+1 to n do

begin

Perm(i+1);

k:=p[i]; p[i]:=p[j]; p[j]:=k

end;

Perm(i+1);

{циклический сдвиг элементов i..n влево}

k:=p[i];

for j:=i to n-1 do p[j]:=p[j+1];

p[n]:=k

end

end;{Perm}

begin {Permutations}

Perm(1)

end;

begin {Main}

readln(n);

for i:=1 to n do p[i]:=i;

a:=p; {массив a может быть заполнен произвольно}

Permutations(n)

end.

Заметим, что в данной программе массив p можно было и не использовать, а переставлять непосредственно элементы массива a.

Билет№38 Алгоритм генерации всех подмножеств.(пример в тетрадке)

При решении олимпиадных задач чаще всего заранее неизвестно, сколько именно элементов исходного множества должно входить в искомое подмножество, то есть необходим перебор всех подмножеств. Однако, если требуется найти минимальное подмножество, то есть состоящее как можно из меньшего числа элементов (или максимальное подмножество), то эффективнее всего организовать перебор так, чтобы сначала проверялись все подмножества, состоящие из одного элемента, затем из двух, трех и т. д. элементов (для максимального подмножества — в обратном порядке). В этом случае, первое же подмножество, удовлетворяющее условию задачи и будет искомым и дальнейший перебор следует прекратить. Для реализации такого перебора можно воспользоваться, например, процедурой cnk, описанной в предыдущем разделе. Введем в нее еще один параметр: логическую переменную flag, которая будет обозначать, удовлетворяет текущее сочетание элементов условию задачи или нет. При получении очередного сочетания вместо его печати обратимся к процедуре его проверки check, которая и будет определять значение флага. Тогда начало процедуры gen следует переписать так:

procedure gen(m,L:integer);

var i:integer;

begin

if m=0 then

begin

check(p,k,flag);

if flag then exit

end

else...

Далее процедура дословно совпадает с предыдущей версией. В основной же программе единственное обращение к данной процедуре следует заменить следующим фрагментом:

k:=0;

flag:=false;

repeat

k:=k+1;

cnk(n,1,flag)

until flag or (k=n);

if flag then print(k)

else writeln('no solution');

Очевидно также, что в основной программе запрос значения переменной k теперь не производится. 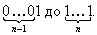Существует также альтернативный подход к перебору всех подмножеств того или иного множества. Каждое подмножество можно охарактеризовать, указав относительно каждого элемента исходного множества, принадлежит оно данному подмножеству или нет. Сделать это можно, поставив в соответствие каждому элементу множества 0 или 1. То есть каждому подмножеству соответствует n-значное число в двоичной системе счисления (строго говоря, так как числа могут начинаться с произвольного количества нулей, которые значащими цифрами не считаются, то следует заметить, что в соответствие ставятся n- или менее -значные числа). Отсюда следует, что полный перебор всех подмножеств данного множества соответствует перебору всех чисел в двоичной системе счисления от

Теперь легко подсчитать и количество различных подмножеств данного множества. Оно равно 2n – 1 (или 2n, с учетом пустого множества). Таким образом, сопоставляя два способа перебора всех подмножеств данного множества, мы получили следующую формулу: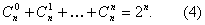

То есть, в рамках сделанной выше оценки на количество допустимых вариантов в переборе, мы можем рассмотреть все подмножества исходного множества только при n? 20.

Прежде, чем перейти к рассмотрению программ, соответствующих второму способу перебора, укажем, когда применение этих программ целесообразно. Во-первых, данные программы легко использовать, когда необходимо в любом случае перебрать все подмножества данного множества (например, требуется найти все решения удовлетворяющие тому или иному условию). Во-вторых, когда с точки зрения условия задачи не имеет значения, сколько именно элементов должно входить в искомое подмножество. На примере такой задачи мы и напишем программу генерации всех подмножеств исходного множества в лексикографическом порядке. Задача взята из книги [5].

Условие. Дан целочисленный массив a[1..N] (N? 20) и число M. Найти подмножество элементов массива a[i1], a[i2],...a[ik] такое, что 1? i1 < i2 < i3 <... < ik? N и a[i1] + a[i2] +... + a[ik] = M.

Решение. В качестве решения приведем процедуру генерации всех подмножеств, которые можно составить из элементов массива и функцию проверки конкретного подмножества на соответствие условию задачи.

function check(j:longint):boolean;

var k:integer; s:longint;

begin

s:=0;

for k:=1 to n do

if ((j shr (k-1))and 1)=1 {данное условие означает, что в

k-й справа позиции числа j, в 2-й системе, стоит 1}

then s:=s+a[k];

if s=m then

begin

for k:=1 to n do

if ((j shr (k-1))and 1)=1 then write(a[k]:4);

writeln

end

end;

procedure subsets(n:integer);

var q,j:longint;

begin

q:=1 shl n; {таким образом мы помещаем в q число 2^n}

for j:=1 to q-1 do {цикл по всем подмножествам}

if check(j) then exit

end; Заметим, что если все элементы в массиве положительные, то, изменив порядок рассмотрения подмножеств, решение приведенной выше задачи можно сделать более эффективным. Так, если сумма элементов какого-либо подмножества уже больше, чем M, то рассматривать подмножества, включающие его в себя уже не имеет смысла. Пересчет же сумм можно оптимизировать, если каждое следующее сгенерированное подмножество будет отличаться от предыдущего не более, чем на один элемент (такой способ перечисления подмножеств показан в [2]). Приведенная же программа чрезвычайно проста, но обладает одним недостатком: мы не можем ни в каком случае с ее помощью перебирать все подмножества множеств, состоящих из более, чем 30 элементов, что обусловлено максимальным числом битов, отводимых на представление целых чисел в Турбо Паскале (32 бита). Но, как уже было сказано выше, на самом деле, перебор всех подмножеств у множеств большей размерности вряд ли возможен за время, отведенное для решения той или иной задачи.

Билет №20 Операторы цикла.

Операторы, предназначенные для многократного (циклического) выполнения заданной последовательности команд, называются операторами цикла. Они всегда имеют заголовок цикла, определяющий число повторений, и тело цикла-повторяеммое действие. Переменная-счетчик должна быть объявлена перед логическим блоком, в котором этот оператор расположен, т. Е. если этот оператор цикла используется внутри подпрограммы, то в качестве счетчика должна выступать локальная переменная. Переменная-счетчик – переменная типа integer (может использоваться перечисляемый тип). Должна быть объявлена перед использованием. Начальное значение, конечное значение – начальное и конечное значение, того же типа (могут быть заданы операторами). Повторяемые операторы(тело цикла) – один или несколько произвольных операторов языка Делфи. Первоначально, до выполнения цикла значение счетчика берется равным «начальное значение». «Конечное значение» - определяет значение счетчика, при котором тело цикла будет выполнено в последний раз. Условие управляющее работой оператора FOR, проверяется перед выполнением тела цикла и если условие не выполняется, то повторяемые операторы не выполнятся ни разу. Выполнив очередной раз тело цикла, счетчик увеличивает свое значение на 1. Затем происходит проверка, если счетчик не превышает конечного значения, то цикл вычислений повторяется, в противном случае работа оператора цикла завершается. Если в начальном или конечном находятся вычисляемые выражения, то вычисление происходит однократно при первом проходе. Пример: вычислим сумму чисел от 1 до 100. В языке Delphi есть другая форма оператора цикла:

for переменная-счетчик:= начальное значение downto конечное значение do повторяемые операторы;

Значение счетчика в этом случае будет уменьшаться на единицу. Оператор цикла записывается так:

For(переменная- счетчик):=(начальное выражение)-1 to(конечное выражение) do повторяемое действие;

Билет№21

В языке программирования часто применяются функции, которые помогают вычислить значение переменной. Она всегда указывается перед той программой, в которой используется, а не после.

Процесс объявления функции достаточно сложен, он выглядит в общих чертах так: «function имя (параметр1:тип1,..,параметрК:тип:к):тип;». Сначала указывается слово «function», которое в языке делфи означает, что далее будет помещена инструкция, которая позволяет реализовать функцию программы. После слова «function» указывается имя функции, оно не обходима для того, чтобы к функции могла обратится программа. Далее после именя в круглых скобках помещается описание функции, где указываются параметря. Параметрами именуются те значения, которые используются для проведения вычислений. Параметры схожи с обычными переменными «var», но они указываются в заголовке функции, а не втом разделе, где чаще всего помещаются переменные «var». Точное значение той переменной, которая задана функцией, определяется только при запуске работы программы. После того, как все программы будут указаны, происходит указание типа значения, т.е. того значения, которое возвратит функция после проведения основных расчетов и вычислений. Объявление функции в общем виде: function Имя (параметр1: тип1,..., параметрК: типК): Тип; var// здесь объявления локальных переменных

begin// здесь инструкции функции

Имя:= Выражение;

end;

где: function — зарезервированное слово языка Delphi, обозначающее, что далее следуют инструкции, реализующие функцию программиста;

имя — имя функции. Используется для перехода из программы к инструкциям функции; параметр — это переменная, значение которой используется для вычисления значения функции. Отличие параметра от обычной переменной состоит в том, что он объявляется не в разделе объявления переменных, который начинается словом var, а в заголовке функции. Конкретное значение параметр получает во время работы программы в результате вызова функции из основной программы; тип — тип значения, которое функция возвращает в вызвавшую ее программу.

Примечание: слово var ставится перед именем параметра в том случае, если параметр используется для возврата значения из функции в вызывающую ее программу.

Билет№22. Объявление процедур.

В общем виде объявление процедуры выглядит так: procedure Имя (var параметр1: тип1;... var параметрК: типК); var // здесь объявление локальных переменных

Begin // здесь инструкции процедуры

end;

где:

procedure — зарезервированное слово языка Delphi, обозначающее, что далее следует объявление процедуры;

имя — имя процедуры, которое используется для вызова процедуры;

параметр K — формальный параметр, переменная, которая используется в инструкциях процедуры. Слово var перед именем параметра не является обязательным. Однако если оно стоит, то это означает, что в инструкции вызова процедуры фактическим параметром обязательно должна быть переменная.

Параметры процедуры используются для передачи данных в процедуру, а также для возврата данных из процедуры в вызвавшую ее программу. 2 способа объявления параметров процедуры:

— Без var, например procedure my(a:real) -- В этом случае процедура возвращает неизмененное значение параметра C var, например procedure my(var a:real) - В этом случае процедура возвращает измененное значение параметра

Пример.

Procedure MyProc(var a: integer; b: integer);

Begin

// a меняется, b остается исходным

a:= a + b; // Прибавляем к a значение b

b:= 1; // b меняется только внутри процедуры

End;

Дата добавления: 2015-04-24