Эксцентрисит эллипса

Определение. называется отношение c ⁄ a, где с — половина расстояния между фокусами, а — большая полуось эллипса.Эксцентриситет обозначают буквой ε: ε = c⁄ a.

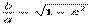
Из равенства легко получается геометрическое истолкование эксцентриситета эллипса. При очень малом ε числа а и b почти равны, т.е. эллипс близок к окружности. Если же ε близко к единице, то число b весьма мало по сравнению с числом а и эллипс сильно вытянут вдоль большой оси. Эксцентриситет эллипса характеризует меру вытянутости эллипса.

Соотношения для фокальных расстояний эллипсаУбедимся в том, что если координаты точки удовлетворяют каноническому уравнению эллипса, то сумма расстояний этой точки до двух точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами. Для этого, очевидно, достаточно показать, что величины r1 и r2 для любой точки, координаты которой удовлетворяют уравнению эллипса, удовлетворяют соотношению r1 + r2= 2·a.

Так как по определению с < a и | х | < a, то выражение в скобках под знаком корня положительно, поэтому

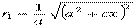
Аналогично найдём

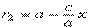
Складывая фокальные расстояния, получим r1 + r2 = 2·aЧто и требовалось доказать. Таким образом, эллипс — линия второго порядка. Замечание. Если а = b, то уравнение эллипса принимает вид x2 + y2= a2. Это уравнение окружности радиуса а. Т.О. окружность — частный случай эллипса. Заметим, что эллипс можно получить из окружности радиуса а, если сжать ее в а ⁄ b раз вдоль оси Оу. Оси симметрии эллипса называются его осями, а центр симметрии (точка пересечения осей) — центром эллипса. Точки, в которых эллипс пересекает оси, называются его вершинами. Вершины ограничивают на осях отрезки, равные 2·а и 2·b. Если а ≥ b, величины а и b называются соответственно большой и малой полуосями эллипса.

Дата добавления: 2015-04-24