Вопрос 17. Определение. Две прямые, перпендикулярные большой оси эллипса и расположенные симметрично относительно центра на расстоянии а⁄ ε от него

Директрисы эллипса

Определение. Две прямые, перпендикулярные большой оси эллипса и расположенные симметрично относительно центра на расстоянии а⁄ ε от него, называются директрисами эллипса (здесь, а — большая полуось, ε — эксцентриситет эллипса).Так как для эллипса ε < 1, то a ⁄ ε > a. Отсюда следует, что правая директриса расположена правее правой вершины эллипса, а левая — общее свойство, присущее эллипсу.

Аналогично доказывается для левого фокуса эллипса.

Каноническое уравнение гиперболы

Гиперболой называется ГМТ плоскости модуль разности расстояний которых до двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная

Определение. Расстояние от произвольной точки М плоскости до фокуса гиперболы называется фокальным радиусом точки М.Обозначения: – фокусы гиперболы, – фокальные радиусы точки М.По определению гиперболы, точка М является точкой гиперболы тогда и только тогда, когда – 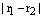постоянная величина. Эту постоянную принято обозначать 2а: Заметим, что. .По определению гиперболы, его фокусы есть фиксированные точки, поэтому расстояние между ними есть также величина постоянная для данной гиперболы.Определение. Расстояние между фокусами гиперболы называется фокусным расстоянием

Обозначение: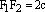

Из треугольника 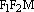следует, что 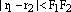т.е.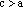

Обозначим через b число равное т. е.

Определение. Отношение

называется эксцентриситетом гиперболы. Введем на данной плоскости систему координат, которую мы будем называть канонической для гиперболы.Определение. Ось, на которой лежат фокусы гиперболы, называется фокальной осью или действительной осью гиперболы.

Каноническое уравнение гиперболы.В канонической для гиперболы системе координат уравнение гиперболы имеет вид 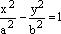Канонические для гиперболы оси координат называются главными осями гиперболы.Определение. Начало канонической для гиперболы системы координат называется центром гиперболы.

Свойства: Свойство 10.6. Гипербола не имеет общих точек с осью Oy, а ось Ox пересекает в двух точках A (a; 0) и B (–a; 0), которые называются вершинами гиперболы. Доказательство.Отрезок AB называется действительной осью гиперболы, его длина равна 2a. Число a называется действительной полуосью гиперболы, число b – мнимой полуосью.

Свойство 10.7. Гипербола имеет две взаимно перпендикулярные оси симметрии.

Свойство 10.8. Гипербола имеет центр симметрии.Доказательство.Центр симметрии гиперболы называют центром гиперболы.

Свойство 10.9. Гипербола пересекается с прямой y = kx при 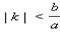в двух точках. Если

то общих точек у прямой и гиперболы нет.

Дата добавления: 2015-04-24